文章结构
- 如何理解贪心算法
- 贪心算法实例分析
- 使用贪心算法实现哈夫曼编码
- 源码地址
- 说明
算法中基本的算法思想有:贪心算法、分治算法、回溯算法、动态规划。这些算法思想并不是具体的算法,他们是用来指导我们设计具体的算法和编码的算法思想。这篇文章我们开始看看贪心算法和它的实际应用,贪心算法有很多经典的应用:哈夫曼编码、Prim和Kruskal最小生成树算法、Dijkstra单源最短路径算法
1、如何理解贪心算法
贪心算法的思想是:每次都做出当前最优的选择,通过多步选择得出最终的最优解。它适合解决上一步的选择不会影响下一步的选择的问题。如果上一步的选择会影响下一步的选择,则使用贪心算法不一定能求出最优解。
1.1 能够使用贪心算法求解的问题举例
问题:假如我们有一个能够容纳100Kg物品的袋子,可以装各种物品,不管物品的体积。现在我们有5种豆子,每种豆子的总重量和总价值各不相同。那如何往背包里面装这些豆子,使得最后背包里物品的总价值最大呢?
我们一眼就能知道这个问题的解法,先求出每种豆子的单价,然后从单价高的豆子开始装,装完单价高的,再去装次高的,直到袋子装满为止。
这个问题就适合用贪心算法来解,实际上上面的做法体现的就是贪心算法的思想(每次都做出当前最优的选择)。这里第一步选择装单价最高的豆子之后,不会影响第二步去选择装次高的豆子的选择,同样第二步也不会影响第三步去选择单价排名第三的豆子。
1.2 不能使用贪心算法来求解的问题举例
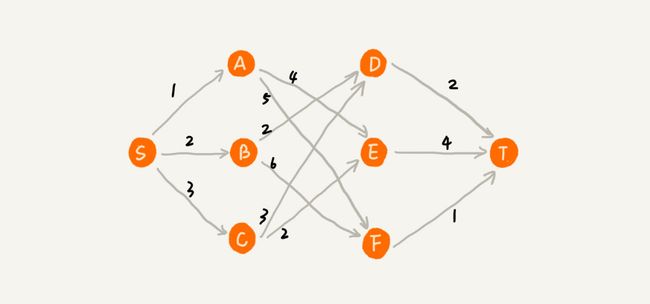
问题:假如我们要在一个有权图中,从顶点S开始,找一条到顶点T的最短路径。
贪心算法的解决思路是,每次都选择一条根当前顶点相连的权最小的边(每次都做出当前最优的选择),直到找到顶点T。按照这种思路,我们求出的最短路径是S->A->E->T,路径长度1+4+4=9;而实际的最短路径是S->B->D->T,路径长度2+2+2=6 。
为什么这里贪心算法得不到最优解呢?我们第一步从S->A和第一步从S->B,下一步面对的顶点和边是不一样的。也就是我们前面的选择会影响后面的选择,所以得不出最优解。
2、贪心算法实例分析
接下来,我们再看几个能够使用贪心算法求最优解的问题。
2.1 分糖果
假设我们有m个糖果和n个小孩,糖果的个数比小孩的个数少,糖果的重量不等,每个小孩对糖果大小的需求也不同,问如何分别糖果能尽可能满足最多数量的孩子的需求。
我们用贪心算法怎么来解决这个问题呢?我们先用最小的糖果来满足对糖果需求最小的孩子的需求,然后再去从剩下的糖果中找最小的糖果满足需求次小的孩子,按照这个思路,直到没有糖果可以满足小孩的需求了为止。
2.2 钱币找零
假设我们有1元、2元、5元、10元、20元、50元、100元面额的纸币各对应c1、c2、c5、c10、c20、c50、c100张。当我们要支付k元的时候,我们如何支付,使得使用的钱币数量最小。
我们用贪心算法怎么来解决这个问题呢?先用面额大,然后在用面额小一点的,依次类推,最后剩下的用1元来补
2.3 求一个非负数移除K个数字之后的最小值
在一个非负数a中,我们希望从中移除k个数字,让剩下的数字值最小,如何选择移除哪k个数字呢?
使用贪心算法来求解这个问题?每一次移除都使当前的数字是能得到的最小值:从高位开始,和低一位的数字比较,如果高位大,则移除高位,如果地位大,则拿着地位和后面的继续比较,直到高位大于低位时,移除高位。移除k个数就重复这个过程k次。
3、使用贪心算法实现哈夫曼编码
3.1 什么是哈夫曼编码
哈夫曼编码是一种十分有效的编码方法,广泛应用于数据压缩中,其压缩率通常在20%~90%之间。哈夫曼编码通过采用不等长的编码方式,根据字符频率的不同,选择不同长度的编码,对频率越高的字符采用越短的编码实现数据的高度压缩。这种对频率越高的字符采用越短的编码来编码的方式应用的就是贪心算法的思想。
哈夫曼编码具体是什么呢?我们采用一个实例来具体看一下。
假如我们有一个包含1000个字符的文件,每个字符占1个byte(1byte=8bits),则存储这100个字符一共需要8000bits,是否有更节省空间的存储方式呢?
如果我们统计一下这1000个字符中总共有多少种字符,原来需要8bit是来表示一个字符,我们使用更少的位数来表示这些字符,则可以减少存储空间。假设这1000个字符中总共有a、b、c、d、e、f共6种字符,则我们只需要使用3个二进制位来表示,那存储这1000个字符就只需要3000bits,比原来更节省存储空间。
a(000)、b(001)、c(010)、d(011)、e(100)、f(101)
有没有比这种方式更节省存储空间的编码方式呢?那就是哈夫曼编码,哈夫曼编码是怎么编码的呢?它会根据字符出现的频率给与字符不等长的编码,频率越高的字符编码越短,频率越高的字符编码越长。当然它不能像等长编码一样直接按固定长度去读取二进制位,翻译成字符,为了能够准确读取翻译字符,它要求一个字符的编码不能是另外一个字符的前缀。
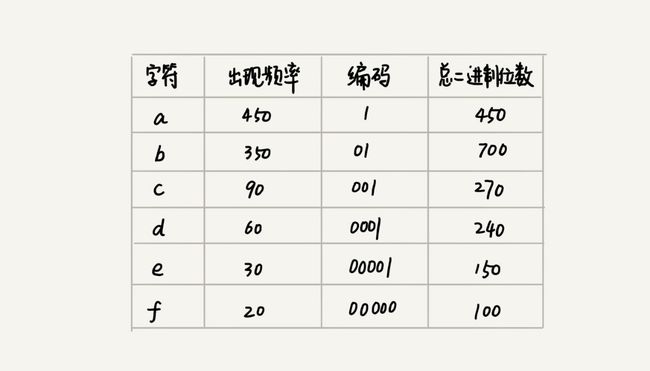
假设a、b、c、d、e、f这6个字符出现的频率依次降低,则我们可以给与他们这样的编码
a(1)、b(01)、c(001)、d(0001)、e(00001)、f(00000)
字符频率和编码,每种字符需要的总的存储位数如图,我们可以看到使用哈夫曼编码来存储这1000个字符只需要2100bits,相同的方式下,比等长bit压缩更节省空间了。
哈夫曼编码的思想不难理解,但是我们如何根据字符出现的频率的不同,给不同的字符进行不同长度的编码呢?
3.2 哈夫曼编码实现过程
哈夫曼编码的实现过程如下:
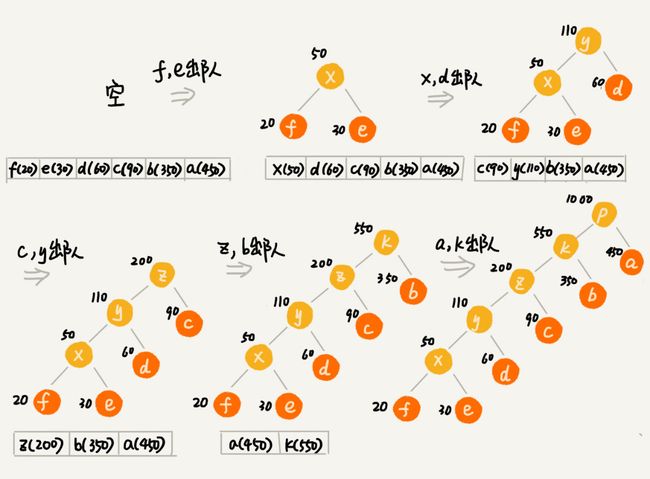
- 将每个字符看做一个节点,以频率的大小作为权重,将所有的字符放到优先级队列中
- 从优先级队列中取两个权重最小的节点,创建一个新的节点作为他们的父节点,父节点的权重为两个字节的权重之和,然后将父节点插入优先级队列中。然后再从优先级队列中取出两个权重最小的节点,创建一个他们的父节点,权重等于两个子节点之和,并插入优先级队列中。重复这个过程直到优先级队列中只有一个节点为止。
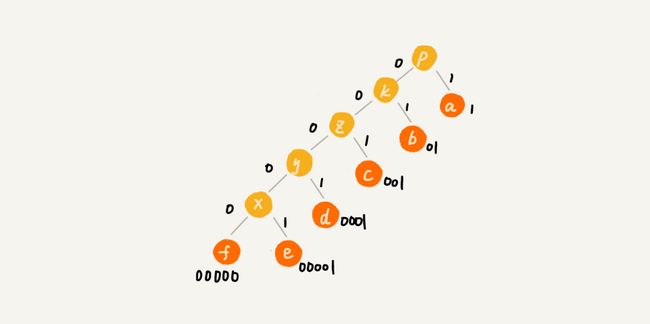
- 优先级队列中只有一个节点的时候,哈夫曼树就创建好了,所有的字符对应的节点都在这颗哈夫曼树的叶子结点上,然后我们开始编码,从根节点开始,指向左子节点的边,我们统统标记为0,指向右子节点的边,我们通过标记为1,从根节点到叶子节点的路径就是叶子节点对应的哈夫曼编码
上面的例子的计算编码的过程图示如下:
3.2 代码实现
- 构建哈夫曼树
- 获取哈夫曼编码
- 将编码转换成字符串
public class HuffmanTree {
/**
* 创建哈夫曼树
*
* @param list
* @param
* @return
*/
public static Node createTree(List> list) {
if (list == null) {
return null;
}
PriorityQueue queue = new PriorityQueue<>();
for (int i = 0; i < list.size(); i++) {
queue.add(list.get(i));
}
while (queue.size() > 1) {
Node left = queue.poll();
Node right = queue.poll();
Node node = new Node(left.pow + right.pow, left, right);
queue.add(node);
}
return queue.poll();
}
/**
* 获取哈夫曼编码(编码这里使用字符串表示)
*
* @param node
* @param
* @return
*/
public static Map getCode(Node node) {
if (node == null) {
return null;
}
Map map = new HashMap<>();
if (node.left != null && node.left != null) {
List codes = new ArrayList<>();
traverse(node, map, codes);
} else {
map.put(node.item, "0");
}
return map;
}
private static void traverse(Node node, Map map, List codes) {
if (node.left == null && node.right == null) {
StringBuilder builder = new StringBuilder();
for (int i = 0; i < codes.size(); i++) {
builder.append(codes.get(i));
}
map.put(node.item, builder.toString());
}
//左子树
if (node.left != null) {
codes.add("0");
traverse(node.left, map, codes);
codes.remove(codes.size() - 1);
}
//右子树
if (node.right != null) {
codes.add("1");
traverse(node.right, map, codes);
codes.remove(codes.size() - 1);
}
}
/**
* 根据哈夫曼编码,解析出字符串
*
* @param map
* @param codeStr
* @param
* @return
*/
public static String reCode(Map map, String codeStr) {
if (map == null) {
return "";
}
//将key和value倒过来
Map map2 = new HashMap<>();
for (T key : map.keySet()) {
map2.put(map.get(key), key);
}
StringBuilder builder = new StringBuilder();
while (codeStr.length() > 0) {
for (String key : map2.keySet()) {
if (codeStr.startsWith(key)) {
builder.append(map2.get(key));
codeStr = codeStr.replaceFirst(key, "");
break;
}
}
}
return builder.toString();
}
public static class Node implements Comparable {
T item;
int pow;
Node left;
Node right;
public Node() {
}
public Node(T item, int pow) {
this.item = item;
this.pow = pow;
}
public Node(int pow, Node left, Node right) {
this.pow = pow;
this.left = left;
this.right = right;
}
@Override
public int compareTo(Node o) {
return pow - o.pow;
}
}
}
测试
/**
* 验证编码与反编码
*/
@Test
public void test2() {
int size = 20;
//创建原始的数据
char[] chars = getChars(size);
//统计字符出现的频率,构建字符节点
List> list = getNodes(size, chars);
print(list, " org node:");
//创建哈夫曼树
HuffmanTree.Node root = HuffmanTree.createTree(list);
//获取哈夫曼编码(这里以字符串表示二进制)
Map codeMap = HuffmanTree.getCode(root);
print(codeMap, "node code:");
//输出原始数据
System.out.println(" orgStr:" + new String(chars));
//编码原始数据
StringBuilder codeBuilder = new StringBuilder();
for (int i = 0; i < size; i++) {
Character ch = chars[i];
codeBuilder.append(codeMap.get(ch));
}
String codeStr = codeBuilder.toString();
System.out.println("code:" + codeStr);
//解析编码
String reCodeStr = HuffmanTree.reCode(codeMap, codeStr);
System.out.println("recodeStr:" + reCodeStr);
}
测试结果
org node:{a:1},{e:2},{f:3},{h:3},{j:1},{k:2},{n:1},{r:1},{t:1},{v:2},{w:1},{x:1},{z:1},
node code:{a:0010},{e:011},{f:101},{h:110},{j:0000},{k:1110},{n:0100},{r:0001},{t:11110},{v:100},{w:11111},{x:0101},{z:0011},
orgStr:fxafkzhfkvnhvehjwter
code:101010100101011110001111010111101000100110100011110000011111111100110001
recodeStr:fxafkzhfkvnhvehjwter
我们可以看到编码能够再次转换成原始的字符串,说明我们设计的哈夫曼编码算法是正常的
4、源码地址
完整的源码和测试用例,请查看github之贪心算法
5、说明
文中图片来源:极客时间,王争《数据结构与算法之美》