统计思维导图与常用公式

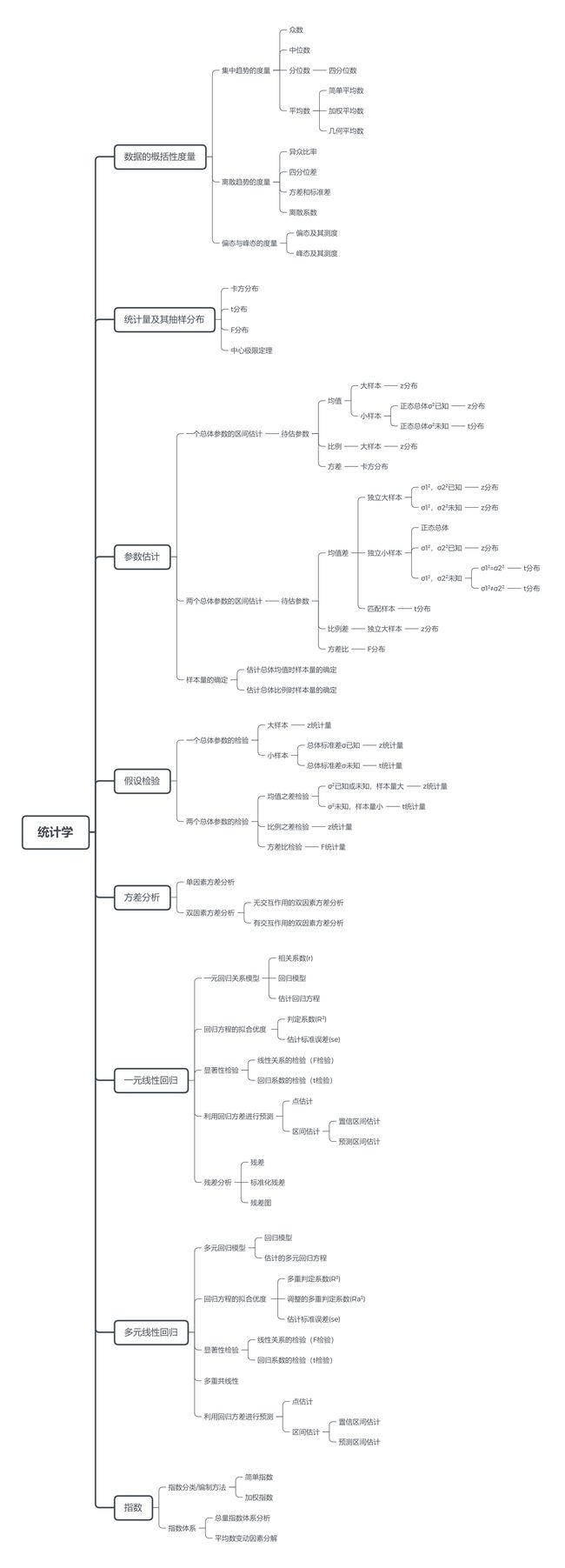
数据的概括性度量

• 集中趋势的度量
  众数（mode）：一组数据中出现次数最多的变量（EXCEL函数：MODE(number1,number2,……）。
  中位数（median）：一组数据排序后处于中间位置上的变量，中位数位置=(n+1)/2（EXCEL函数：MEDIAN(number1,number2，……）。
  四分位数（quartile）：一组数据排序后处于25%和75%位置上的值，
  ,（EXCEL函数：QUARTILE(array,quart))。
  平均数（mean）：一组数据相加后处于数据个数得到的结果。
    简单平均数（simple mean）：
    加权平均数（weighted mean）： （:权重与频数的乘积）
    几何平均数（geometric mean）： (GEOMEAN(number1,number2,……））

• 离散趋势的度量
  异众比率（variation ration）：值非众数组的频数占总频数的比例。(为变量值的总频数,为众数组的频数）
  四分位差（quartile deviation）：也称内距或四分位距,它是上四分位分数与下四分位分数之差。
  方差（variance）：各变量值预期平均数离差平方的平均数。
  标准差（standard deviation）：方差的平方根。
  离散系数（coefficient of variation）：一组数据的标准差与其相应的平均数之比。

• 偏态与峰态的度量
  偏态（skewness）：它是对数据分布对称性的测度。
  偏态系数（coefficient of skewness）：,是样本标准差的三次方。（EXCEL函数：SKEW(number1，number2，……），样本数少于3个或者标准差为0，则返回错误值#DIV/0!）
    偏态的强度：1.偏态系数=0，数据的分布是对称的；
          2.偏态系数>1或者<-1,高度偏态分布；
          3.偏态系数位于[0.5,1]或者[-1,-0.5],中等偏态分布。
    偏态的方向判断：1.SK为正值时，正离差值较大，正偏或者右偏；
            2.SK为负值时，负离差值较大，负偏或者左偏。

峰态（kurtosis）：它是对数据分布平峰或尖峰程度的测度。
峰态系数（coefficient of kurtosis）：,是样本标准差的四次方。（EXCEL函数：KUPT(number1，number2，……），样本数少于4个或者标准差为0，则返回错误值#DIV/0!）
   峰态的测度：1.K=0,正态分布；
         2.K>0,尖峰分布，数据的分布更集中；
         3.K<0,扁平分布，数据的分布更分散。

统计量及其抽样分布

• 中心极限定理（central limit theorem）
  设从均值为、方差为（有限）的任意一个总体中抽取样本量为的样本,当充分大时，样本均值的抽样分布近似服从均值为、方差为的正态分布。

参数估计

一个总体参数的区间估计

• 总体均值的区间估计：

            不同情况下总体均值的区间估计

总体分布	样本量	σ已知	σ未知
正态分布	大样本（）
正态分布	小样本（）
非正态分布	大样本（）

• 总体比例的区间估计
  比例的区间估计只讨论在大样本的情况下，由样本比例的抽样分布可知，当样本量足够大时，比例的抽样分布可用正态分布近似。
  总体比例的置信区间为：

• 总体方差的区间估计
  方差的区间估计只讨论正态总体方差的问题。根据样本方差的抽样分布可知，样本方差服从自由度为n-1的分布。因此，用分布构造总体方差的置信区间。
  总体方差σ²在1-置信水平下的置信区间为：
  

两个总体参数的区间估计

• 两个总体均值之差的区间估计

参数	点估计量（值）	标准误差	（1-)%的置信区间	假定条件
两个总体 均值之差				（1）独立大样本 (≥30,≥30) （2）,已知
两个总体 均值之差				（1）独立大样本 (≥30,≥30) （2）,未知
两个总体 均值之差				（1）两个正态总体 （2）独立小样本 (＜30,＜30) （3）,未知但相等
两个总体 均值之差				（1）两个正态总体 （2）独立小样本 (＜30,＜30) （3）,未知且不相等
两个总体 均值之差				匹配大样本 (≥30,≥30)
两个总体 均值之差				（1）两个正态总体 （2）匹配小样本 (＜30,＜30)

• 两个总体比例之差的区间估计

参数	点估计量（值）	标准误差	（1-)%的置信区间	假定条件
两个总体 比例之差				（1）两个二项总体 （2）匹配小样本 ( )

• 两个总体方差比的区间估计

参数	点估计量（值）	标准误差	（1-)%的置信区间	假定条件
两个总体 方差比		（不要求）		两个正态总体

样本量的确定

• 估计总体均值时样本量的确定
  由于估计误差,因此可以推断出确认样本量的公式如下：
  

• 估计总体比例时样本量的确定
  由估计误差可以推导出重复抽样或无限总体抽样条件下确认样本量的公式如下：
  

假设检验

• 两类错误

项目	没有拒绝	拒绝
为真	1-（正确决策）	(弃真错误)
为伪	（取伪错误）	（正确决策）

• 假设的检验流程
  1.提出原假设与备择假设;
  2.计算统计分布量；
  3.将统计分布量与显著性水平比较（如值）：若,不拒绝;
                       若,拒绝。

• 利用P值进行决策
  P值反映了观察到的实际数据与原假设之间不一致的概率，可以有效避免以上两类错误。
  在事先确认好显著性水平后，如,则在双侧检验中，P>0.025（）不能拒绝原假设；反之，P<0.025则拒绝原假设；在单侧检验中，P>0.05不能拒绝原假设；P<0.05则拒绝原假设。

• 单侧检验
  左单侧检验称为下限检验，右单侧检验称为上限检验。

一个总体参数的检验
在一个总体参数的检验中，用到的检验统计量主要有三个：统计量，统计量，统计量。统计量和统计量主要用于均值和比例的检验，统计量则用于方差的检验。

检验参数	条件要素	检验统计量
总体均值检验	大样本
总体均值检验	小样本 （σ已知）
总体均值检验	小样本 （σ未知）
总体比例检验	大样本
总体方差检验	大样本

两个总体参数的检验

检验参数	条件要素	检验统计量
均值之差 检验	样本量大 σ²已知或未知
均值之差 检验	样本量小 σ²未知,且
均值之差 检验	样本量小 σ²未知,且
比例之差 检验	服从二项分布
方差比 检验	两个正态总体

方差分析

单因素方差分析
总平方和（sum of squares for total）：
组间平方和（sum of squares for factor A）:
组内平方和（sum of squares for error）：

EXCEL方差分析表：

误差来源	平方和SS	自由度df	均方MS	F值	P值	F临界值
组间（因素影响）	SSA	k-1	MSA	MSA/MSE
组内（误差）	SSE	n-k	MSE
总和	SST	n-1

表格分析：1.若F值>F临界值，则拒绝原假设，表明有显著差异；
     2.若F值      3.若P<,则拒绝,若P>,则不拒绝。

• 关系强度的度量
  反映自变量和因变量的关系程度的大小记为:
  

• 方差分析中的多重比较
  方差分析中的比较值记为LSD：
  
  如果,则拒绝，如果,则不拒绝。

双因素方差分析

• 无交互作用的双因素方差分析
  第一项行因素产生的误差平方和，记为SSR:
  第二项列因素产生的误差平方和，记为SSC:
  
  EXCEL方差分析表：

误差来源	平方和SS	自由度df	均方MS	F值	P值	F临界值
行因素	SSR	k-1	MSR
列因素	SSC	n-k	MSC
误差	SSE	（k-1）*（r-1）	MSE
总和	SST	kr-1

表格分析：
1.，拒绝原假设,表明行之间有显著差异，反之则不拒绝原假设，表明行之间没有明显差异；
2.，拒绝原假设,表明列之间有显著差异，反之则不拒绝原假设，表明列之间没有明显差异；
3.如果P-value<，拒绝原假设，P-value>，不拒绝原假设。

关系强度的测度：

• 有交互作用的双因素方差分析
  
  EXCEL方差分析表：

误差来源	平方和SS	自由度df	均方MS	F值	P值	F临界值
行因素	SSR	k-1	MSR
列因素	SSC	n-k	MSC
交互作用	SSRC	（k-1）*（r-1）	MSRC
误差	SSE	kr(m-1)	MSE
总和	SST	kr-1

表格分析：
1.行因素的P-value<,则拒绝原假设，表明行之间有显著差异，反之，不拒绝原假设，表明行之间没有显著差异；
2.列因素的P-value<,则拒绝原假设，表明列之间有显著差异，反之，不拒绝原假设，表明列之间没有显著差异；
3.交互作用的P-value<，则拒绝原假设，表明相互作用有显著影响，反之，不拒绝原假设，表明相互作用没有显著影响。

一元线性回归

相关系数（correlation coefficient）：根据样本数据计算的度量两个变量之间线性关系强度的统计量(CORREL(Array1,Array2))。

EXCEL一元线性回归表：

回归统计
Multiple R
R Square
Adjusted R Square
标准误差
观测值	n

方差分析

	SS	df	MS	F值	P值	Significance F
回归	SSA	k-1	MSA	MSA/MSE
残差	SSE	n-k	MSE
总计	SST	n-1

	Coefficients	标准误差	t Stat	P-value	Lowe 95%	Upper 95%
Intercept
X Variable 1

表分析：
1.回归方程：;
2.r=1时，x与y之间为完全正线性相关关系，r=-1时，x与y之间为完全负线性相关关系；r区间为(0,1)时，x与y之间为正线性相关关系，r区间为(-1,0)时，x与y之间为负线性相关关系。
3.的值表明x与y之间的拟合强度，的值越接近1，表明x与y相关性越强，拟合性越好。
4.标准误差可以用来度量各实际观测点在直线周围散布状况的一个统计量，说明判断结果的误差范围。
5.线性关系检验：若,拒绝,表明两个变量之间的线性关系是显著的；若,不拒绝，没有证据表明两个变量之间的线性关系显著（除此之外，还需要判断P值与之间的大小以确定是否拒绝,EXCEL表中的显著性F（Significance F）就是用于检验的P值）。
6.回归系数的检验：t(t Stat)>，拒绝原假设，表明该变量是显著性影响要素（判断P值方法与前面相同）。
7.点估计：代入自变量到回归方程获得相应的因变量。
8.置信区间估计：
9.预测区间估计：，预测区间要比置信区间更宽一些。

多元线性回归

EXCEL多元线性回归表：

回归统计
Multiple R
R Square
Adjusted R Square
标准误差
观测值	n

方差分析

	SS	df	MS	F值	P值	Significance F
回归	SSA	k-1	MSA	MSA/MSE
残差	SSE	n-k	MSE
总计	SST	n-1

	Coefficients	标准误差	t Stat	P-value	Lowe 95%	Upper 95%
Intercept
X Variable 1
X Variable 2
X Variable 3
……	……

表分析：
1.回归方程：;
2.r=1时，x与y之间为完全正线性相关关系，r=-1时，x与y之间为完全负线性相关关系；r区间为(0,1)时，x与y之间为正线性相关关系，r区间为(-1,0)时，x与y之间为负线性相关关系。
3.为调整多重判定系数，表明x与y之间的拟合强度，的值越接近1，表明x与y相关性越强，拟合性越好。
4.标准误差可以用来度量各实际观测点在直线周围散布状况的一个统计量，说明判断结果的误差范围。
5.线性关系检验：若,拒绝,表明两个变量之间的线性关系是显著的；若,不拒绝，没有证据表明两个变量之间的线性关系显著（除此之外，还需要判断P值与之间的大小以确定是否拒绝,EXCEL表中的显著性F（Significance F）就是用于检验的P值）。
6.回归系数的检验：t(t Stat)>，拒绝原假设，表明该变量是显著性影响要素（判断P值方法与前面相同）。

指数

简单综合指数：,,代表质量指标，代表数量指标；代表质量指标指数，代表数量指标指数。
加权综合指数：, ，其中代表的是权数。
（1）拉氏指数：,, 代表质量指标指数，代表数量指标指数，和分别表示基期和报告期的质量指标值；和分别表示基期和报告期的数量指标值
（2）帕氏指数：,

• 总体指数分析
  实际分析中比较常用的是基期权数加权的数量指数（拉氏指数）和报告期权数加权的质量指数（帕氏指数）形成的指数体系，该指数体系可表示为：
  
  因素影响的差额之间的关系为：