Matplotlib绘制函数的等高线与三维图像

前言

  本篇文章记录一下函数的等高线及其三维图像的可视化方法。本例绘制的函数为$$f(x,y)=x{e}^{-(x^2+y^2)}$$

1. 网格点

  在绘制曲线之前，先了解一下网格点的绘制。比如绘制一个3x3的网格，那么就需要9个坐标点：

(0,2)-----(1,2)-----(2,2)

(0,1)-----(1,1)-----(2,1)

(0,0)-----(1,0)-----(2,0)

  将其x轴和y轴坐标分开表示：

# x轴:
[[0, 1, 2],
[0, 1, 2], 
[0, 1, 2]]
# y轴:
[[0, 0, 0],
[1, 1, 1], 
[2, 2, 2]]

  在numpy中可以使用np.meshgrid()来生成网格点：

import numpy as np
import matplotlib.pyplot as plt

# 10x10
x = np.linspace(-1.5, 1.5, num=10)
y = np.linspace(-1.5, 1.5, num=10)

# generate grid
X, Y = np.meshgrid(x, y)
plt.plot(X, Y, marker='.', linestyle='')
plt.grid(True)
plt.show()

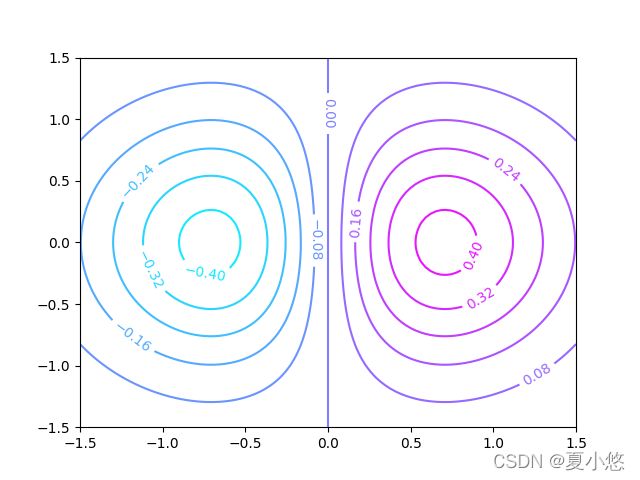
2. 等高线

  绘制等高线需要的数据有点的坐标位置(x, y)以及坐标的高度z，高度z就是将坐标点(x, y)带入函数$f(x,y)$中计算得到的，在matplotlib中可以使用plt.contour()来绘制：

import numpy as np
import matplotlib.pyplot as plt


x = np.linspace(-1.5, 1.5, num=100)
y = np.linspace(-1.5, 1.5, num=100)
X, Y = np.meshgrid(x, y)
f = X * np.exp(-X**2 - Y**2)

fig = plt.figure()
plt.xlim(-1.5, 1.5)
plt.ylim(-1.5, 1.5)

# draw
ax = plt.contour(X, Y, f, levels=10, cmap=plt.cm.cool)
# add label
plt.clabel(ax, inline=True)
# plt.savefig('img1.png')
plt.show()

# add color
plt.contourf(X, Y, f, levels=10, cmap=plt.cm.cool)
# plt.colorbar()
# plt.savefig('img1.png')
plt.show()

  更多的api参数请参考官方文档。

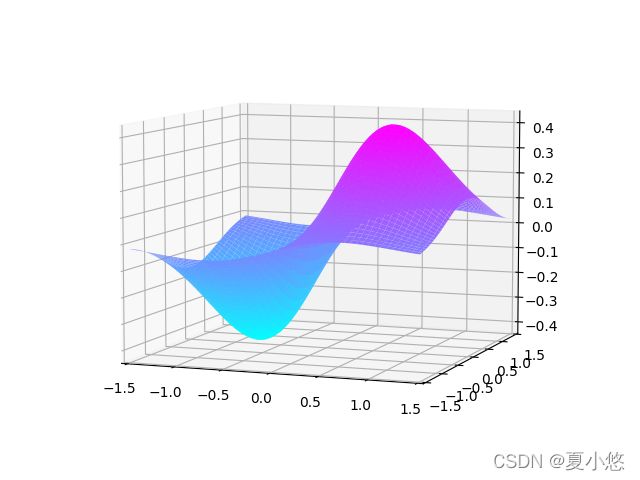
3. 三维图像

  函数的三维图像的绘制需要的数据与等高线一样，即坐标位置(x, y)以及坐标的高度z，在matplotlib中可以使用mpl_toolkits.mplot3d来绘制：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


x = np.linspace(-1.5, 1.5, num=100)
y = np.linspace(-1.5, 1.5, num=100)
X, Y = np.meshgrid(x, y)
f = X * np.exp(-X**2 - Y**2)

fig = plt.figure()
ax = Axes3D(fig)
plt.xlim(-1.5, 1.5)
plt.ylim(-1.5, 1.5)

ax.plot_surface(X, Y, f, cmap=plt.cm.cool)
# plt.savefig('img1.png')
plt.show()

  有关mpl_toolkits.mplot3d的使用可以参考官方文档；

  更多的颜色搭配可参考matplotlib的colormap官方手册。