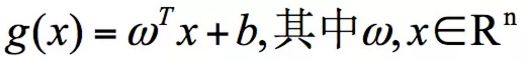机器学习笔记-Task05-支持向量机SVM
前言
本文是通过学习AI蜗牛车的【白话机器学习】算法理论+实战之支持向量机(SVM)及诸如吴恩达、B站白板推导之SVM系列等资料后写的笔记。
1. SVM简介
SVM是Support Vector Machine的简称,即支持向量机。它是一种二分类算法。在深度学习出现之前,SVM因为其在处理二分类问题上的优越表现,成为最流行的分类算法之一。
在研究领域,常说SVM有三宝,即:
- 间隔margin
- 对偶
- 核函数
这个我们在下文会逐一说明为何上述三个直接代表了SVM的全部。
此外,SVM可以分为三类:
- Hard-Margin SVM (硬间隔SVM)
- Soft_Margin SVM (软间隔SVM)
- Kernel SVM (核SVM,非线性SVM)
2. SVM工作原理
2.1 分类小例子
如图1所示,桌子上面放了红蓝两种球,如果让你用一根棍子将他们分开,相信你最后提交的答案肯定与图2类似。
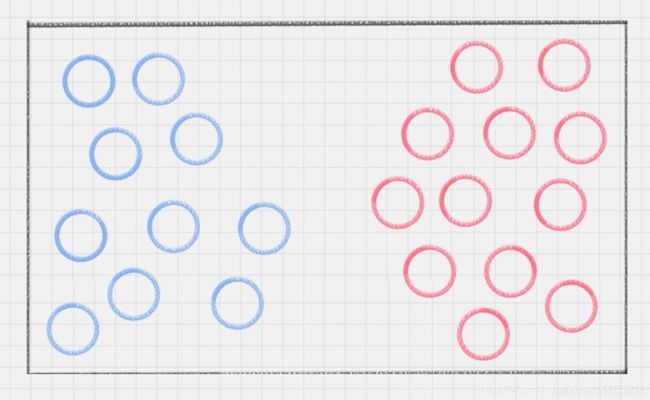
| 图片1(来源:AI蜗牛车) |
|---|
| 图2(图片来源:AI蜗牛车) |
|---|
但是,当两种球的分布变成图3时,显然一根笔直的棍子已经无法达到分割的效果,这个时候,你肯定希望有一根如图4所示的弯曲的棍子,那样就可以达到分割效果了。但是这样的棍子在现实生活中是不存在。
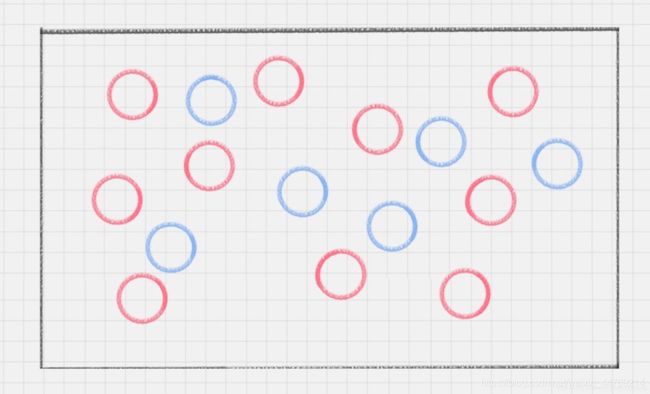
| 图3(图片来源:AI蜗牛车) |
|---|

| 图4(图片来源:AI蜗牛车) |
|---|
这里你可能会灵机一动,猛拍一下桌子,这些小球瞬间腾空而起,如下图所示。在腾起的那一刹那,出现了一个水平切面,恰好把红、蓝两种颜色的球分开。如下图所示。
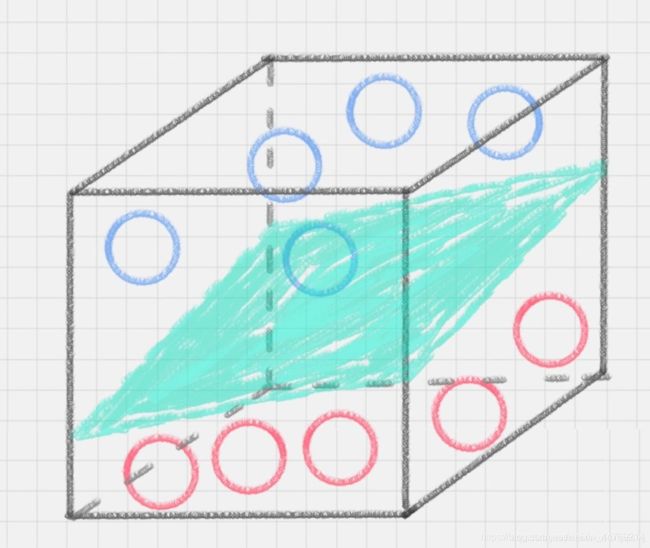
| 图5(图片来源:AI蜗牛车) |
|---|
2.2 工作原理
对于上述分类的例子,不同的人肯定会有不同的分割方法,也就是说在红蓝两种球之间,存在无数条直线,可以达到目前的分类效果。问题是,哪一种是最好的呢?
对于下图6而言,A和B均过于靠近红蓝样本,如果样本数变多,很可能出现错误的情况(如:蓝色球跑到了B的右侧)这样一来,模型的泛化能力或者鲁棒性就会很差。三条线之间,显然是C最好。如果在多维空间,C就代表了一个面。我们在SVM中我们称之为超平面。
我们目标是找到一条最中间的超平面,使其离正负样本点的距离都足够大,这样一来,模型就不会因为样本数的增多,而出现错误的情况。

| 图6(图片来源:AI蜗牛车) |
|---|
- ω \omega ω、x 是 n 维空间里的向量,其中 x 是函数变量; ω \omega ω是法向量。法向量这里指的是垂直于平面的直线所表示的向量,它决定了超平面的方向。
SVM 就是帮我们找到一个超平面,这个超平面能将不同的样本划分开,同时使得样本中的点到这个分类超平面的最小距离(即分类间隔)最大化。
伪代码:
- 如果用distance表示样本点( x i , y i x_{i},y_{i} xi,yi)到超平面的距离,那么对于大小为N的样本集,当超平面给定时,这个距离distance就会有N个,我们要找的就是最小的那个距离。
- 当超平面一变,就会出现另一个最小距离;
- 循环
- 在这些最小距离集中,找到一个最大的最小距离。
最后这一问题,将会变成一个凸优化问题,就可以转为拉格朗日的对偶问题。
2.3 数学推导
2.3.1 拉格朗日乘子法与KKT条件
待补充
2.3.2 推导过程
2.4 相关术语
当超平面求出来之后,就会得到下面的效果,这里涉及到几个术语:
- 分离超平面:就是那个能把样本分开的那个最优超平面了
- 支撑超平面:是分离超平面平移到极限位置之后的那两条直线
- 分离间隔:支撑超平面之间的距离
- 支持向量:就是那两个极限位置的样本。(在决定分离超平面时,只有支持向量在起作用,而其他实例点不起作用。由于支持向量在确定分离超平面中起着决定性作用,所以将这类模型叫做支持向量机)

3. 三类SVM介绍
3.1 硬间隔SVM
当样本像上文介绍的那样,线性可分且一定要达到完全将红蓝两种球分开的效果时,此时的算法硬间隔SVM算法。
3.2 软间隔SVM
但是实际生活中,数据会存在一些噪声,导致分类不能完全正确,可能存在个别点的错误。这个时候,如果允许出现这样的小错误,则是软间隔SVM算法。
3.3 核SVM(非线性SVM)
除了线性数据,实际使用过程中,还存在非线性数据的情况。去下图所示。当红蓝两种球呈圆形分布时,不论是多高级的分类器,只要映射函数是线性的,就没法处理,SVM 也处理不了 。
这个时候我们就会想到如果也能像前面拍桌子那样,使小球的分布出现在一个高维空间的话,那是不是就可以很容易的分开了。不过这里的“拍桌子”有一个专业名词:核函数。它可以将样本从原始空间映射到一个更高维的特质空间中,使得样本在新的空间中线性可分。
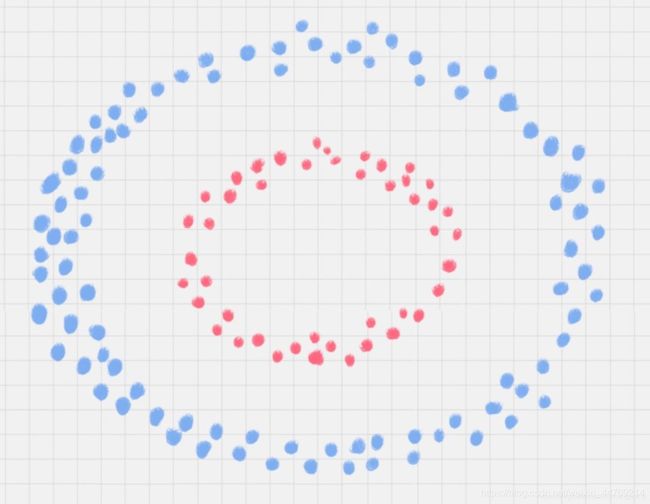
核函数的技巧,类似于下图这样:
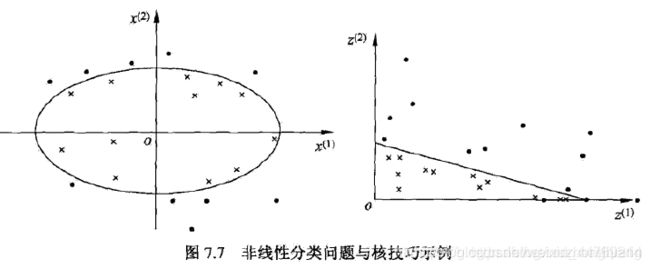
所以,在非线性SVM中,核函数的选择就是影响其性能的最大因素。常用的核函数有:
- 线性核
- 多项式核
- 高斯核
- 拉普拉斯核
- Sigmoid核
- 或者上述核函数的组合
4.如何求解多分类问题
SVM 本身是一个二值分类器,最初是为二分类问题设计的,也就是回答 Yes 或者是 No。而实际上我们要解决的问题,可能是多分类的情况,比如对文本进行分类,或者对图像进行识别等。
针对这种情况,我们可以将多个二分类器组合起来形成一个多分类器,常见的方法有“一对多法”和“一对一法”两种。
4.1 一对多法
一对多法 假设我们要把物体分成 A、B、C、D 四种分类,那么我们可以先把其中的一类作为分类 1,其他类统一归为分类 2。这样我们可以构造 4 种 SVM,分别为以下的情况:
- 样本 A 作为正集,B,C,D 作为负集;
- 样本 B 作为正集,A,C,D 作为负集;
- 样本 C 作为正集,A,B,D 作为负集;
- 样本 D 作为正集,A,B,C 作为负集。
特点:
这种方法,针对 K 个分类,需要训练 K 个分类器,分类速度较快,但训练速度较慢,因为每个分类器都需要对全部样本进行训练,而且负样本数量远大于正样本数量,会造成样本不对称的情况,而且当增加新的分类,比如第 K+1 类时,需要重新对分类器进行构造。
4.2 一对一法
一对一法 一对一法的初衷是想在训练的时候更加灵活。我们可以在任意两类样本之间构造一个 SVM,这样针对 K 类的样本,就会有 C k 2 C_{k}^{2} Ck2类分类器。比如我们想要划分 A、B、C 三个类,可以构造 3 个分类器:
- 分类器 1:A、B;
- 分类器 2:A、C;
- 分类器 3:B、C。
- 当对一个未知样本进行分类时,每一个分类器都会有一个分类结果,即为 1 票,最终得票最多的类别就是整个未知样本的类别。
优点:
如果新增一类,不需要重新训练所有的 SVM,只需要训练和新增这一类样本的分类器。而且这种方式在训练单个 SVM 模型的时候,训练速度快。
缺点:
分类器的个数与 K 的平方成正比,所以当 K 较大时,训练和测试的时间会比较慢。
5.代码实例Sklearn-乳腺癌检测
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn import svm
from sklearn import metrics
from sklearn.preprocessing import StandardScaler
#读取数据
data = pd.read_csv('breast_cancer-master/data.csv')
print(data.head())
print(data.columns)
print(data.describe())
#id列没有意义,删除
data.drop('id',axis = 1,inplace=True)
#替换数据值,恶性M为1,良性B为-1。
data.loc[data['diagnosis'] == 'M','diagnosis'] = 1
data.loc[data['diagnosis'] == 'B','diagnosis'] = -1
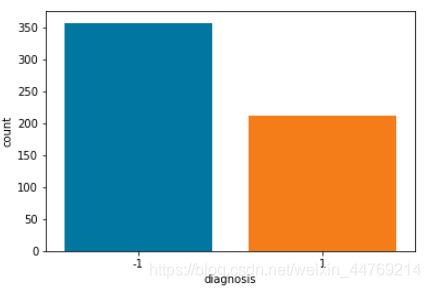
sns.countplot(data['diagnosis'],label="Count")
plt.show()
# 将特征字段分成3组
features_mean= list(data.columns[1:11])
features_se= list(data.columns[11:21])
features_worst=list(data.columns[21:31])
#用热力图呈现features_mean字段之间的相关性
corr = data[features_mean].corr()# 计算相关性
plt.figure(figsize=(14,14))
# annot=True显示每个方格的数据
sns.heatmap(corr, annot=True)
plt.savefig('corr.png')#保存图片
plt.show()
train, test = train_test_split(data, test_size = 0.3)# in this our main data is splitted into train and test
# 抽取特征选择的数值作为训练和测试数据
train_X = train[features_mean]
train_y=train['diagnosis']
test_X= test[features_mean]
test_y =test['diagnosis']
# 采用Z-Score规范化数据,保证每个特征维度的数据均值为0,方差为1
ss = StandardScaler()
train_X = ss.fit_transform(train_X)
test_X = ss.transform(test_X)
# 创建SVM分类器
model = svm.SVC()
# 用训练集做训练
model.fit(train_X,train_y)
# 用测试集做预测
prediction=model.predict(test_X)
print('准确率: ', metrics.accuracy_score(prediction,test_y))
![]()
参考资料
- 【白话机器学习】算法理论+实战之支持向量机(SVM)
- 简书【贪心科技:学习SVM,这篇文章就够了!(附详细代码)】