数据结构——算法竞赛中熠熠生辉的两朵金花—“栈“和“队列“

前言：为学日进，为道日损。与诸君携手共勉

人生好似一个小小的队列呀，春夏秋冬年年轮回，早中晚夜天天循环。变化的是时间，不变的是我们对未来执著的信念！

栈

栈的定义和基本操作

栈的定义

栈(stack)是限定仅在表尾进行插入和删除操作的线性表
我们把允许插入和删除的一端称为栈顶(top),另一端称为(bottom),不含任何数据元素的栈称为空栈。栈又称为后进先出(Last In First Out)的线性表，简称LIFO结构。

注意:栈是一个线性表。也就是说栈是具有线性关系的，拥有它自己的直接前驱和直接后继。只是，栈是一种特殊的线性表，只能在表尾进行插入和删除操作，这里的表尾通常也被叫做栈顶(top)

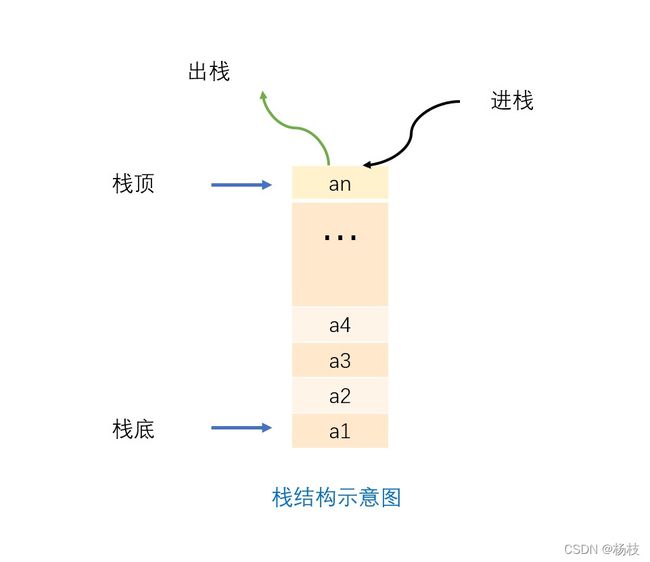
栈的基本操作

栈的插入操作（push），叫做进栈，也称压栈、入栈。类似于将子弹压入弹夹
栈的删除操作（pop），叫做出栈，有的也叫做弹栈。如同将弹夹中的子弹取出
进栈示意图：

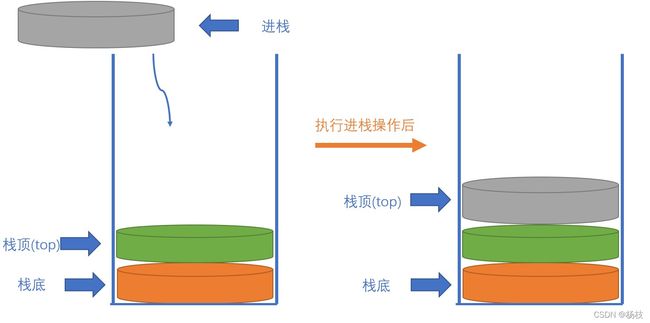
出栈示意图：

进入下一个模块啦~⏩

栈的存储和实现

栈数组实现——算法竞赛必备

栈在算法竞赛中也算是常客了。只是使用它的时候需要注意，我们是用数组模拟栈的思想来实现栈。那，为什么要用数组了？我们平时学的都是结构体+指针实现的呀~

就笔者自己使用的C++而言，因为一般竞赛中的测试数据都要拉到极致，比如十万、一百万，假如使用结构体的方式，在new这十万、一百万的空间的时候，可能就超时了。包括下文的队列也是同样的道理，在竞赛中，建议用数组模拟。结构体加指针的玩法，笔者盲猜是用在工程中优化代码效率的✌
只是C++选手也可以偷偷懒，直接调用C++标准库中提供的库函数

下面就从一道例题来引入怎么用数组快速的模拟栈吧~
例题描述：

⌛原题传送门

参考代码(C++版本)

#include 

using namespace std;

const int N = 100010;

int m;
int stk[N];     //用于模拟栈的数组
int tt;         //尾指针

int main()
{
    cin >> m;
    while (m -- )
    {
        string op;
        int x;

        cin >> op;
        if (op == "push")
        {
            cin >> x;
            stk[ ++ tt] = x;    //尾指针向后移动，实现进栈
        }
        else if (op == "pop") tt -- ; // 尾指针向前移动，剔除数组末尾元素，实现出栈
        else if (op == "empty") cout << (tt ? "NO" : "YES") << endl;
        else cout << stk[tt] << endl;
    }

    return 0;
}

进栈(push)

数组模拟的栈，进栈代码很简单，只有一行…

		stk[ ++ tt] = x;    //尾指针向后移动，实现进栈

操作的原理图如下：

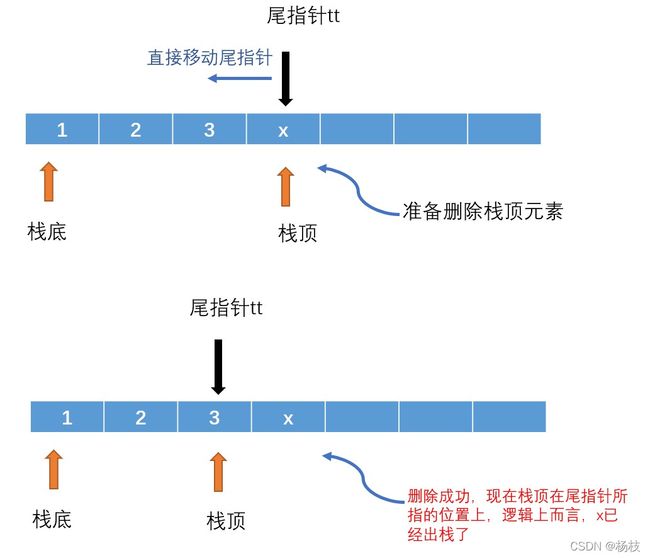
出栈(pop)

出栈操作就更短了~

		 else if (op == "pop") tt -- ; // 尾指针向前移动，剔除数组末尾元素，实现出栈

获取信息——栈顶元素和栈是否为空

获取栈顶元素也就是获取尾指针tt所指的空间中的信息，因为是数组模拟的，所以直接将tt放到数组里面

		 else cout << stk[tt] << endl;

判断栈是不是空栈是通过数组下标实现的。假如现在尾指针tt在栈底(索引为0)的位置，这个栈就是空栈。对于这道题而言,取巧用了三元运算符

  			else if (op == "empty") cout << (tt ? "NO" : "YES") << endl;

说什么？掌握啦。嗯好，那咱们进入下一个模块~⏩

栈的链式存储结构及实现——工程开发和期末应试必备

下面的内容了，是数据结构用在工程上和期末考试的卷子上的

栈的链式存储结构实际上就是一个单链表，叫做链栈。插入和删除操作只能在链栈的栈顶进行。栈顶指针Top应该在链表的哪头？

假如按照正常逻辑，放在链表的尾部，插入操作要从头结点开始，挨着挨着遍历过去，到最后一个元素，也就是栈顶就可以实现插入。
删除操作了？删除操作其实是没有办法进行的，因为链表的删除要知道被删除结点的前一个结点的信息，我们没法从链表的尾结点倒着回去找它的前一个结点，也没有办法确定它的前一个结点的信息，因此删除操作就无法实现。

因此经过前人的总结，将头指针所指的位置当做栈顶对于插入和删除操作都十分方便

链栈类型定义

和单链表相同，定义一个结点类型，类型中的成员变量是数据域和指针域

typedef int Datatype;

typedef struct stacknode{
    Datatype data;				//数据域
    struct stacknode* next; //指针域
}LinkStack;

初始化栈

首先创建一个链栈S，然后通过NULL将这个创建的栈清空。返回被清空后的链栈的地址信息
参考实现代码：

LinkStack* InitStack()
{
    LinkStack* S;
    S = NULL;
    return S;
}

判断栈空

判断一个栈是否为空，若栈为空，则返回1，否则返回0
参考实现代码：

int EmptyStack(LinkStack* S)
{
    if(S == NULL) return 1;
    else return 0;

}

进栈

实现流程：
①将新插入的结点p的指针域指向原栈顶S
②将栈顶S指向新结点p

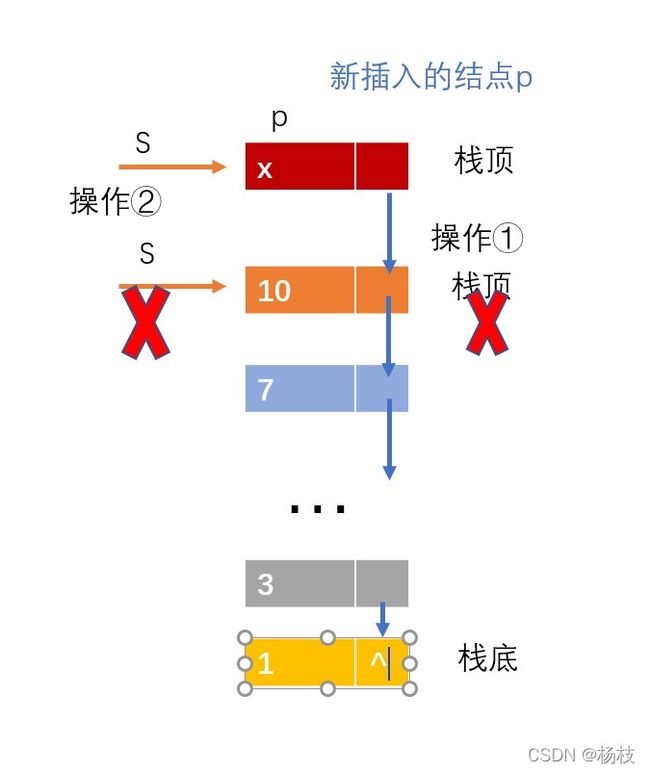
参考实现代码：

LinkStack* push(LinkStack *S,Datatype x)
{
    LinkStack* p;
    p = (LinkStack*)malloc(sizeof(struct stacknode));	//生成新结点 
    p->data = x;			//将x放到新结点的数据域 
    p->next = S; 		//将新结点插入链表的表头之前 
    S = p;  				//让头指针执行这个新插入的p。可以理解为让top指针指向这个新插入的结点

	return S; 			//返回栈顶S 

}

出栈

①p指针指向原栈顶S
② 栈顶S指向其下一个结点
③释放p指针所指的空间

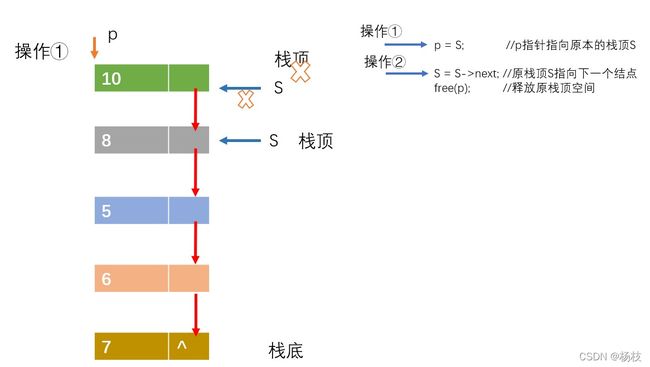
参考实现代码：

LinkStack* pop(LinkStack* S , Datatype *x)
{
    LinkStack* p;
    if(EmptyStack(S))	//先判断栈是否为空栈
    {
        printf("栈为空\n");
        return NULL;
    }else
    {
	    *x = S->data;		//栈顶元素取出来赋值给x 
	    p = S; 				//p指针指向原本的栈顶S 
	    S = S->next;		//原栈顶S指向下一个结点 
	    free(p);			//释放原栈顶空间 
	    return S;			//返回栈顶S 
    }
}

好啦~
链栈的两个核心操作入栈push 和 出栈pop 就没有啦，相信小伙伴已经明白是这么一回事了。下面的获取栈顶元素和输出栈中内容就相对轻松很多啦~

取栈顶元素

参考实现代码：

int GetTop(LinkStack* S,Datatype *x)
{
   
    if(EmptyStack(S))	 //先判断栈是否为空
    {
        printf("栈为空\n");
        return 0;
    }else
    {
        *x = S->data;	//栈顶元素赋值给变量x 
        return 1;
    }

}

显示栈内元素

参考实现代码

void ShowStack(LinkStack *S)
{

    LinkStack *p = S;
    if(p == NULL)
    {
        printf("栈为空\n");
    }else
    {
        printf("从栈顶起，各元素依次为：\n");
        while(p != NULL)
        {
            printf("%d\t",p->data);
            p = p->next;
        }
    }
}

栈的应用举例

"进制转换"领域

以十进制转二进制为例，操作的流程是每次模2取得余数，整数自身除以权重2，从而更新整数自己。
可以考虑是将余数放到数组里，用一个循环反转数组，再用一个循环将新的数组遍历输出，听起来其实还是蛮麻烦的

那么结合栈的先入后出的特性，会不会更好操作了？用push将余数压入栈，再用pop将放到栈里面的余数一个一个的取出来，是不是感觉整体思路都清爽了很多了

实现流程：
用一个循环处理传入的十进制整数x，将它和2取余的结果入栈
用一个循环输出栈中的内容

参考实现代码

//十进制转二进制
void D_B(LinkStack *S,Datatype x)
{
   
    while(x)				 //让余数入栈
    {
        S = push(S,x % 2);
        x /= 2;
    }
    printf("转换后的二进制为：");
    while(!EmptyStack(S))
    {
        S = pop(S,&x);		//依次从栈中弹出每一个余数
        printf("%d",x);		//输入每个余数
    }
}

"表达式求值"领域

因为这个板块有好多习题可以拎出来细细品味，所以笔者想在《算法基础》专栏中更出
比如2020年就有一道真题：2020年ACM-ICPC省赛B题 相同括号配对

栈总结

对于栈而言，最主要是要清楚它先入后出的特性。其次拿捏清楚指向栈顶元素的"指针"，因为无论是数组模拟的栈还是结构体实现的栈，核心操作都是对指针的移动

相信小伙伴已经学会了吧，那咱们进入下一个模块啦~⏩

队列

队列的定义和基本运算

队列的定义

队列是只允许在一端进行插入操作，而在另外一端进行删除操作的线性表
队列是一种先进先出(First In First Out)的线性表，简称FIFO。允许插入的一端称为队尾，允许删除的一端称为队头。

队列的基本运算

队列的存储和实现

队列数组实现——算法竞赛必备

队列在算法竞赛中也是常客了，主流的依旧是使用的数组模拟的队列。原因和栈用数组模拟的原因一致。
队列用得最多，知名度最广的应该是在边权相等的情况下用宽度优先搜索去求最短路径，进而还有拓扑排序等等

下面依旧是从一道例题中引入数组模拟队列
样例描述：

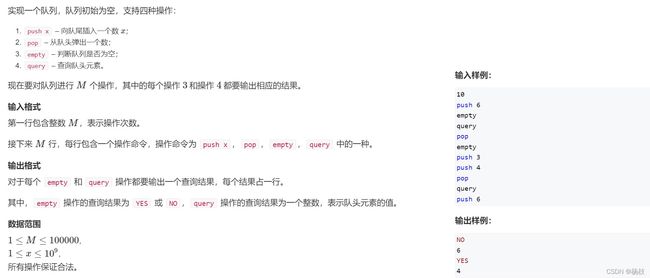
⌛原题传送门

参考实现代码(C++版本)

#include 

using namespace std;

const int N = 100010;

int m;
int q[N];//模拟队列的数组
hh, tt = -1;//队头和队尾

int main()
{
    cin >> m;

    while (m -- )
    {
        string op;
        int x;

        cin >> op;
        if (op == "push")
        {
            cin >> x;
            q[ ++ tt] = x; //移动尾指针实现插入
        }
        else if (op == "pop") hh ++ ; //移动头指针位置，实现删除
        else if (op == "empty") cout << (hh <= tt ? "NO" : "YES") << endl;
        else cout << q[hh] << endl;
    }

    return 0;
}

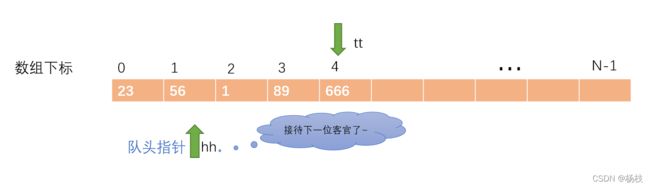
队列的初始状态如下图

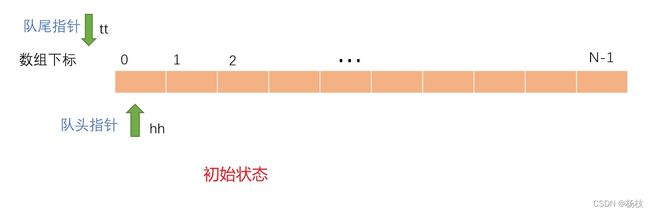
在初始化状态中，队头队尾都放在索引为0的位置也是可以的，那么在后面移动尾指针tt的时候使用后缀++即可。

		//队尾从-1开始
		 q[ ++ tt] = x; //移动尾指针实现插入
		 
		 //变通===> 队尾从0开始
		 q[tt ++] = x; //移动尾指针实现插入

入队

因为本质是数组，所以当有新数据插入的时候，让新数据插入到数组的尾部就可以实现入队操作。

            cin >> x;
            q[ ++ tt] = x; //移动尾指针实现插入

出队

数组模拟的队列中，使用队头指针hh来维护队列中第一个元素的位置。当有元素要出队了，那么通过移动队头指针调整队列的区间，从而确定新的队头。

		else if (op == "pop") hh ++ ; //移动头指针位置，实现删除

新的姿势增加了，那咱们向下一个模块出发啦~⏩

队列链表实现——工程开发和期末应试必备

链队列类型定义

使用结构体加上指针实现的队列在本质上仍旧是线性表中的链表，只是对它开发了新的特性，实现了先进先出(FIFO)的效果。

参考实现代码

typedef int DataType;		//定义DataType为int 型
typedef struct qnode{		//链队列存储类型 
	DataType data;			//定义链队中每个结点的数据域 
	struct qnode *next;		//定义链队中每个结点的指针域 
}LinkListQ; 

typedef struct
{
	LinkListQ *front,*rear; //链队列的队头指针和队尾指针 
}LinkQueue;					

只是对于队列而言，为了实现维护一段队伍的效果，需要额外增加一个队头指针front和一个队尾指针rear

LinkListQ *front,*rear; //链队列的队头指针和队尾指针 

初始化队列

操作流程：
①先建立一个队列的头结点Q，该头结点中有维护队列的队头指针front和队尾指针rear
② 建立一个链队的头结点p,并让其指针域为空
③ 将Q->front 和 Q->rear都指向该头结点并返回指针Q
参考实现代码：

LinkQueue *InitQueue()
{
	LinkQueue *Q;
	LinkListQ *p;
	Q = (LinkQueue *) malloc(sizeof (LinkQueue));  //建立链队列头指针所指的结点 
	p = (LinkListQ *)malloc(sizeof(LinkListQ));		//建立链队列的头结点 
	p->next = NULL;
	Q->front = p;									//Q指针所指的front指针指向p 
	Q->rear  = p;									//Q指针所指的rear指针指向p 
	
	return Q;
}

入队操作

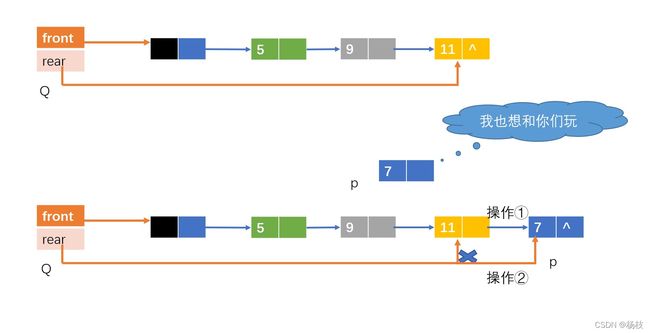
实现流程：
①将新结点插入到队尾，原本队尾的指针域Q->rear->next 指向新结点p(Q->rear->next = p;)
②将队尾Q->rear指向新结点p(Q->rear = p; )
参考实现代码：

//入队函数 
void InQueue(LinkQueue *Q,DataType x)
{
	LinkListQ *p;
	p = (LinkListQ *)malloc(sizeof(LinkListQ));	//生成新的结点
	p->data = x;								//将x存入新结点的数据域 
	p->next = NULL;					
	Q->rear->next = p;							//将新结点插入到链队之后 
	Q->rear = p; 								//队尾指针指向队尾元素 
}

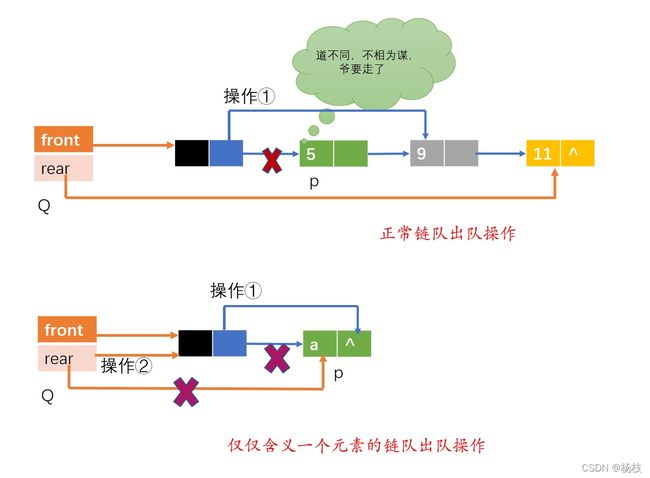
出队操作

操作①：将队头指针的指针域指向原本队头元素的下一个位置的地址（Q->front->next = p->next;）
操作②：当队列中仅含有一个元素的时候，出队后队尾指针指向队头指针所指向的位置(if(p->next == NULL) Q->rear = Q->front)
操作③：释放p指针所指的空间

参考实现代码：

//判断队列是否为空的函数
int EmptyQueue(LinkQueue *Q) 
{
	if(Q->front == Q->rear) return 1;
	else return 0;
}

//出队函数 
int DeQueue(LinkQueue *Q,DataType *x)
{
	LinkListQ *p;
	if(EmptyQueue(Q))  						//调用判空函数，判断当前队列是不是为空
	{
		printf("队空，无法出队任何元素\n")	;
		return 0;
	}else  									//队列不空 
	{
		p = Q->front->next;					//p指向队头元素
		*x = p->data;						//取出队头元素赋值给x
		Q->front->next = p->next;			//队头指针的指针域中存放新队头元素的地址
		if(p->next == NULL)  Q->rear = Q->front; //处理队列中只有一个元素的情况
		free(p);
		return 1;
		 
	}
}

求队头元素

参考实现代码：

int GetFront(LinkQueue *Q,DataType *x) 
{
	if(EmptyQueue(Q))				//调用判空函数，判断当前队列是不是为空
	{
		printf("队列为空，无法获取任何元素");
		return 0;
	}else
	{
		*x = Q->front->next->data;	//将队头元素中存放的数据给x
		return 1; 
	}
}

遍历链队

void ShowQueue(LinkQueue *Q)
{
	LinkListQ *p = Q->front->next;
	if(p == NULL) printf("队列为空，无法显示任何元素\n");
	else
	{
		printf("从队头起，队列中的每个元素是：");
		while(p != NULL)
		{
			printf("%d ",p->data);
			p = p->next;
		}
	}
}

好啦~到这里，链队列的操作就没有啦，核心的了，是出队和入队操作。使用结构体加指针实现的队列，在代码量上确实多了很多

曾经高考考场上笑谈一方，现在只求老师给个重点。就让链栈和链队列在考场上最后绽放一次吧

新的痛苦增加了呀，朋友们

队列的应用举例

"宽度优先搜索(BFS)"方向

队列是宽搜实现的核心结构，因为笔者之前已经详解总结和演示过宽搜，那我这里就不再赘述啦，小伙伴们可以看看这篇文章喔
算法基础系列第三章——层层推进的BFS
假如感觉已经掌握了宽搜的小伙伴，可以考虑去壁咚一下队列在高等图算法中的玩法
算法基础系列第三章——万字精编手把手教你壁咚拓扑排序，让ta乖乖听话~

"优先队列"——堆

优先队列是一种特殊的队列了，优先队列的出队是按照元素的优先级出队，比如，数值最小的先出队，或者数值最大的先出队。优先队列和二叉树结合起来，就又变成了一种神器——堆
同样的，因为笔者之前已经写过和堆相关的内容了，现在就直接推荐小伙伴们去看一看啦~
数据结构——被优先队列玩起来的“树“

队列总结

数组模拟的队列实现和操作都是比较清晰和轻松的，只是有时候需要注意元素假如要进行多次的入队和出队，那么用于实现队列结构的数组开头部分的空间就会被严重浪费，这种情况可以采用"循环队列"的方式优化。笔者这里就不展开讲了，我想在后续的《算法基础》专栏中结合习题进行系统的剖析。

结构体+指针的实现方式就要对指针十分小心，清楚当前的指针是指向谁的

写在最后

编者暂时也阅历有限，可能个别地方考虑不周，若有偏僻，欢迎小伙伴们及时指正喔( ^ - ^ )

持续更新对数据结构的总结和理解ing