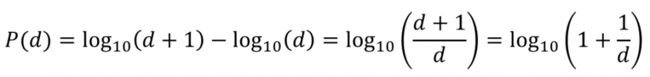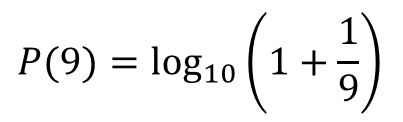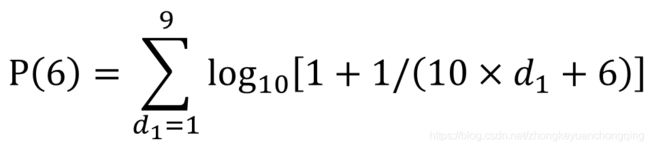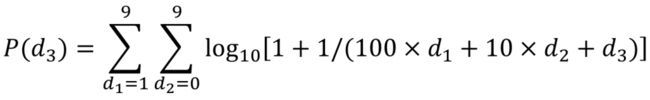本福特定律,也称为本福德法则,说明一堆从实际生活得出的数据中,以1为首位数字的数的出现机率约为总数的三成,接近期望值1/9的3倍。推广来说,越大的数,以它为首几位的数出现的机率就越低。它可用于检查各种数据是否有造假。
要准确的判断数据是否为自然生成还需要计算两个指标,分别为KS值和截止值。然后对两个指标进行对比。如果KS值低于截止值,那么可以判定数据为自然生成,没有经过人工修饰。否则就可能有造假的风险。
KS值是数据的实际概率值与期望概率值差异的最大值,截止值是1.36除以数据条目数的平方根。我们对前面的数据表计算KS值和截止值。
本福德定律加强版
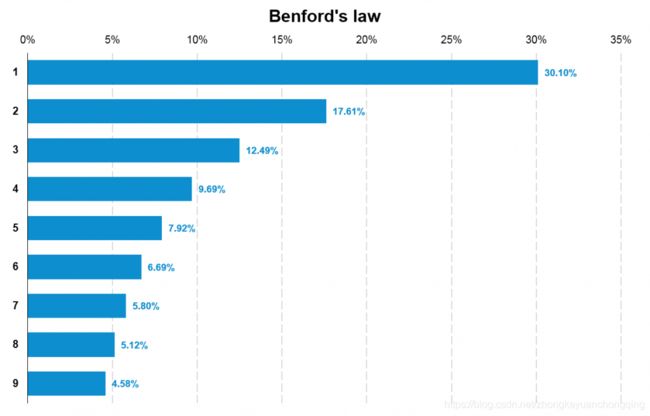
1938年,物理学家Frank Benford发现了一个有趣的数字规律(Benford Law) ——现实生活中数字的首字母是“1”的概率要远远大于“9”。仔细研究后发现,从1~9出现的概率符合对数分布,“1”出现的概率为30.1%,“2”出现的概率为17.6%,而“9”的概率只有4.6%,详细见下图,纵坐标是概率,横坐标是数字。
这是一个令人迷惑,违反直觉的发现,为什么数字的出现概率要这样分布呢? 一个可能的解释是符合这个规律的数据有尺度不变的性质,比如一组数据如果以英寸作为单位时符合Benford规律,那个把这组数据换成厘米为单位时仍然符合Benford规律。换个角度,如果把尺度不变作为基础,那么只有对数分布才能导致尺度不变。虽然这个理由看上去很合理,但只能说是自洽的,仍然没有直接回答“为什么要出现这种分布?”或者“为什么要求尺度不变?”
Benford定律并非符合一切数据,符合的一些数据有:湖的面积,河流的长度,物理学常数,股票指数,电脑文件的大小等等。不符合的有摇奖号码,电话号码等。为什么会这两类数据的差异呢? 一定有更深的规律在其中。
最近,来自北京大学的邵立晶和马伯强提出了自然界中Benford定律的新的理解方式,他们把Benford应用到物理学中常见的三种统计分布中,分别是波尔兹曼-吉布斯分布、玻色-爱因斯坦分布、费米-狄拉克分布,这三种分布分别是经典粒子、玻色子、费米子的分布规律。
邵立晶和马伯强认为波尔兹曼-吉布斯分布和费米-狄拉克分布根据系统的温度,在Benford分布附近周期性的波动(见上图,红线为费米-狄拉克分布,蓝线为波尔兹曼-吉布斯分布,横轴为温度的倒数,纵轴是波动大小),而玻色-爱因斯坦分布不管温度是多少都遵守Benford分布。这么看来Benford定律是物理学的一个基本的特征,可能在自然现象背后扮演着非常基础的角色。
数据造假的甄别在数据分析领域是一个热门的话题,也是对数据分析师的一项挑战。分析数据造假的方法有很多种。我们在前面的系列文章中曾经介绍过两种检验作弊流量的方法。一种是根据历史经验及分布情况的多维度交叉检验,另一种是使用随机森林模型根据已知作弊流量的特征对新流量进行分类及预测。
本篇文章介绍一种神奇的数据检验方法,本福德定律(Benford’s Law)。本福德定律是一种用途广泛的数据检验方法,在安然公司破产和伊朗大选选票甄别中都曾被使用到。本福德定律通过自然生成的数字中1到9的使用频率对数据进行检验。如果你的数据具备一定规模,没有人工设定的最大值和最小值,并且数据本身受人为因素影响较小。那么就可以使用本福德定律对数据进行检验,甄别数据是否经过人为修饰。
本福德定律及公式
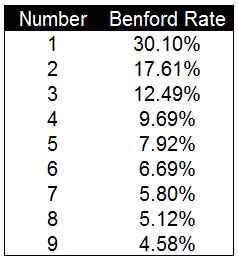
本福德定律中自然生成的数字首位为1的概率为30.10%,2的概率为17.61%,依次递减,首位为9的概率仅为4.58%。依据这一期望概率值我们可以对数据进行检验。以下是本福德定律的计算公式。通过这一公式可以计算出1-9中每个数字出现数据首位的概率。
举例来说,对于数字9下面的公式可以计算出一组自然生成的数字中9出现在数字首位的概率是多少。
我们使用本福德定律公式逐一计算了数字1-9出现在首位的概率。以下是每个数字出现的概率值。后面会根据这一期望的概率值对数据是否进行过人工修改进行甄别。
通过图表可以更较直观的看到本福德定律中每个数字出现的频率以及不同数字间的差异。与我们想象的不同,数字出现的频率并不是均匀分布的。1出现的次数为30.10%而9出现的次数仅为4.58%。
下面我们将使用本福德定律对工作中常见的数据进行检验,甄别数据是否经过人为修饰。
广告展现量数据检验
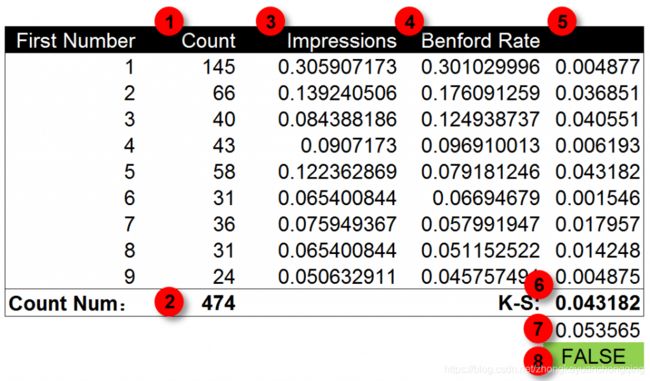
首先检验一组广告曝光数据。下面是某广告一段时间的曝光量数据。我们将每条展现量数据的第一个数字提取出来,通过本福德定律对这组数据进行检验。
第一步计算展现量数据中数字1-9出现的次数。第二步计算所有展现量数据的条目,展现量数据为474条。第三步计算数字1-9出现次数的频率。第四步使用本福德定律计算出数字1-9出现频率的期望值。
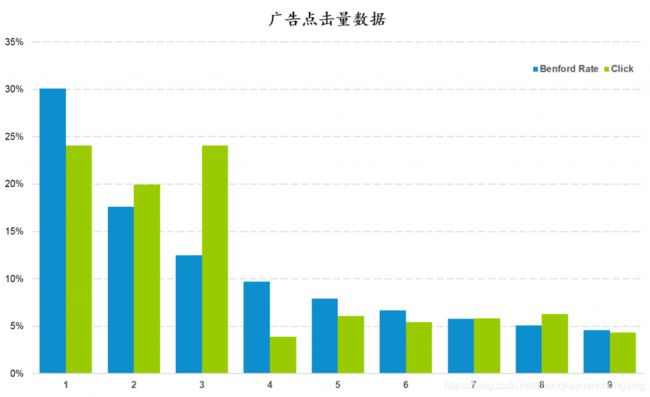
将曝光量数据和本福德定律的期望值绘制到图表中进行对比,可以发现曝光量数据首位数字出现的频率与本福德定律整体上基本一致。在数字2,3和5上略有差异。这个柱状图能说明什么?表明数据符合本福德定律?三个数据点上的差异又说明什么?数据中存在人为修饰吗?
单从实际概览值和图表上我们无法辨别数据是否经过人为修饰。要准确的判断数据是否为自然生成还需要计算两个指标,分别为KS值和截止值。然后对两个指标进行对比。如果KS值低于截止值,那么可以判定数据为自然生成,没有经过人工修饰。否则就可能有造假的风险。
KS值是数据的实际概率值与期望概率值差异的最大值,截止值是1.36除以数据条目数的平方根。我们对前面的数据表计算KS值和截止值。第五步,计算实际概率值与期望概率值的差异。这里我们取差异的绝对值以避免负数的产生。第六步,计算K-S值,经过计算K-S值为0.043,也就是数字5出现频率的差异。第七步,计算截止值,这里的曝光数据共有474条,因此截止值为0.053。第八步,对比K-S值与截止值,K-S值小于截止值。因此数据属于自然生成。没有经过人为修饰。
广告点击量数据检验
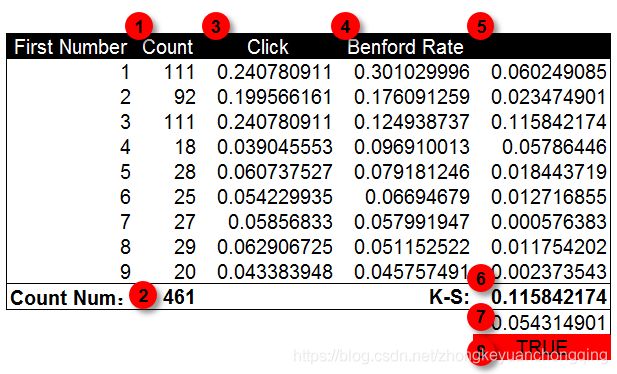
按照前面的方法,我们对同一组广告的点击量数据进行检验。在下面的柱状图中,蓝色为本福德定律的期望概率值,绿色为广告点击量的首位数字分布情况。可以发现在数字1,3和4上实际值与期望值之间存在较大的差异。尤其是在数字3上。但仅根据这几个差异点我们还不能判断数据是否经过人工修饰。
进一步计算K-S值和截止值并进行对比。K-S值为数据点间的最大差异值,这里是0.115。截止值经过计算为0.054。K-S值明显大于截止值。因此可以判断点击量数据是经过人工修饰的可能,需要进一步进行检验。
贷款金额数据检验
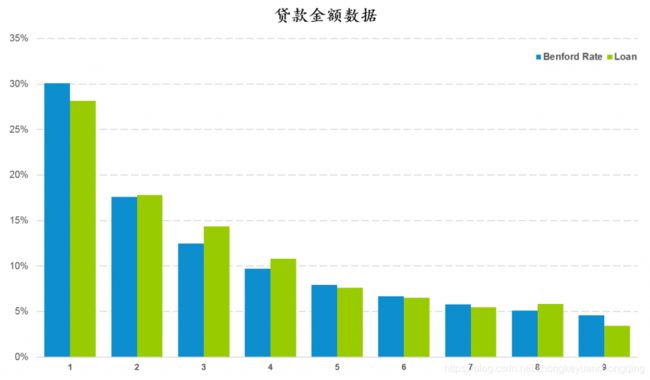
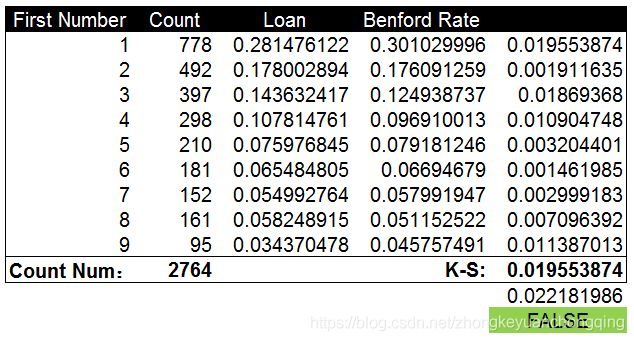
除了广告数据以外,本福德定律还可以在很多场景下对数据进行检验。如贷款金额的数据。下面是一组贷款金额首位数字分布与本福德定律逾期分布的对比图。两者的趋势一致,差异也较小。
通过计算K-S值和截止值并进行对比,K-S值0.019小于截止值0.022。说明贷款金额数据为自然生成,不存在人工修饰。
Excel随机数检验
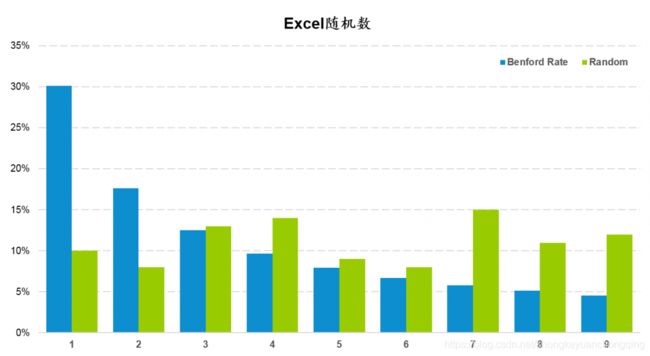
最后,我们人工生成一组”假数据”,看看本福德定律的检验结果。这里使用Excel的随机数函数生成100个随机数。并与本福德定律的期望分布进行对比。很明显,Excel生成的随机数在首位数字上为均匀分布。与本福德定律的期望分布相差甚远。
计算并对比K-S值和截止值也再次证明了均匀分布的数据为人工生成。K-S值0.201大于截止值0.116。
本福德定律加强版
本福德定律除了计算首位数字出现的概率,还有个加强版,可以计算第二位数字甚至第三位数字出现的概率,并通过这些这些期望值对数据进行更加深入和严格的检验。下面是计算第二位数字出现概率的公式。d1表示第一位出现的数字,d2表示第二位出现的数字。
如果我们要计算第二位数字为6的期望值,将数字6代入公式中,如下面截图所示。分别计算1-9每个数字与第二位数字6进行组合时的概率,再进行加总就是数字6作为第二位出现数字的期望概率值。
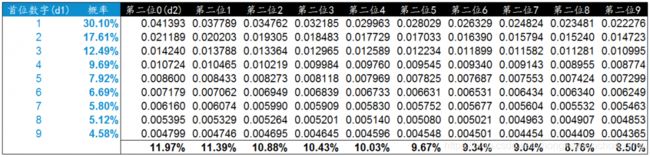
在Excel中实际计算下,蓝色部分为首位数字和出现的概率。后面依次是第二位数字从0-9依次与首位数字组合出现的概率值。我们按列进行汇总就是每个第二位数字出现的概率。
再进一步还可以计算第三位数字出现的概率。方法与计算第二位数字出现的方法类似,只是更为负责一些。下面是计算公式。将0-9的10个数字分别与前两位的各种数字组合在一起计算,然后把每种情况单一数字出现的概率进行汇总,就是这个数字出现在第三位的期望值了。
以第三位数字是0为例,蓝色列表示第一位数字的值,由于第一位不能为0,所以数字范围为1-9。第一行黑色背景为第二位数字的值,从0-9。计算各种组合情况下第三位数字为0的概率,并进行汇总。最终0.1018就是0作为第三位数字出现的概率值。
我们按照同样的方法计算了0-9在第三位出现的概率,并与前面计算的首位和第二位数字出现概率进行汇总生成了下面的数据检验表。通过这个概率分布表可以更加深入的对数据的真实性进行检验。
参考:本福特定律
参考:Benford's Law And A Theory of Everything
参考:使用本福德定律甄别数据造假(Benford’s Law)
参考:自然现象中的Benford规律
参考:使用python训练随机森林模型辨别可疑流量
参考:使用Google Analytics辨别虚假流量
参考:使用Google Analytics辨别虚假流量(二)