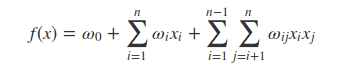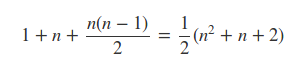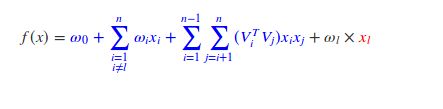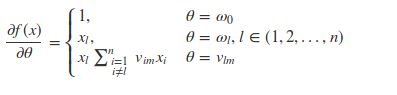1、FM
1.1 背景
1.1.1 线性模型
常见的线性模型,比如线性回归、逻辑回归等,它只考虑了每个特征对结果的单独影响,而没有考虑特征间的组合对结果的影响。
对于一个有n维特征的模型,线性回归的形式如下:
其中(ω0,ω1...ωn)为模型参数,(x1,x2...xn)为特征。
从(1)式可以看出来,模型的最终计算结果是各个特征的独立计算结果,并没有考虑特征之间的相互关系。
举个例子,我们“USA”与”Thanksgiving”,”China”与“Chinese new year”这样的组合特征是很有意义的,在这样的组合特征下,会对某些商品表现出更强的购买意愿,而单独考虑国家及节日都是没有意义的。
1.1.2 二项式模型
我们在(1)式的基础上,考虑任意2个特征分量之间的关系,得出以下模型:
这个模型考虑了任意2个特征分量之间的关系,但并未考虑更高阶的关系。
模型涉及的参数数量为:
对于参数ωi的训练,只要这个样本中对应的xi不为0,则可以完成一次训练。
但对于参数ωij的训练,需要这个样本中的xi和xj同时不为0,才可以完成一次训练。
在数据稀疏的实际应用场景中,二次项ωij的训练是非常困难的。因为每个ωij都需要大量xi和xj都不为0的样本。但在数据稀疏性比较明显的样本中,xi和xj都不为0的样本会非常稀少,这会导致ωij不能得到足够的训练,从而不准确。
1.2 FM
1.2.1 FM基本原理
为了解决上述由于数据稀疏引起的训练不足的问题,我们为每个特征维度xi引入一个辅助向量:
Vi=(vi1,vi2,vi3,...,vik)T∈ℝk,i=1,2,3,...,n (4)
其中k为辅助变量的维度,依经验而定,一般而言,对于特征维度足够多的样本,k<
1.2.2 数据分析
我们的目标是要求得以下交互矩阵W:
由于直接求解W不方便,因此我们引入隐变量V:
如果我们先得到V,则可以得到W了。
现在只剩下一个问题了,是否一个存在V,使得上述式(9)成立。
理论研究表明:当k足够大时,对于任意对称正定的实矩阵W∈ℝn×n,均存在实矩阵V∈ℝn×k,使得W=VVT。
理论分析中要求参数k足够的大,但在高度稀疏数据的场景中,由于 没有足够的样本,因此k通常取较小的值。事实上,对参数k的限制,在一定程度上可以提高模型的泛化能力。
1.2.3参数个数
假设样本中有n个特征,每个特征对应的隐变量维度为k,则参数个数为1+n+nk。
正如上面所言,对于特征维度足够多的样本,k<
1.2.4 计算时间复杂度
下面我们分析一下已经知道所有参数,代入式(6)计算预测值时的时间复杂度。从式(6)中一看,
可以看出时间复杂度是O(kn2)。但我们对上述式子的最后一项作变换后,可以得出一个O(kn)的时间复杂度表达式。
上述式子中的∑ni=1(vilxi)只需要计算一次就好,因此,可以看出上述模型的复杂度为O(kn)。
也就是说我们不要直接使用式(6)来计算预测结果,而应该使用式(10),这样的计算效率更高。
1.2.5 梯度
FM有一个重要的性质:multilinearity:若记Θ=(ω0,ω1,ω2,...,ωn,v11,v12,...,vnk)表示FM模型的所有参数,则对于任意的θ∈Θ,存在与θ无关的g(x)与h(x),使得式(6)可以表示为:
从式(11)中可以看出,如果我们得到了g(x)与h(x),则对于参数θ的梯度为h(x)。下面我们分情况讨论。
* 当θ=ω0时,式(6)可以表示为:
上述中的蓝色表示g(x),红色表示h(x)。下同。
从上述式子可以看出此时的梯度为1.当θ=ωl,l∈(1,2,...,n)时,
此时梯度为xl。
当θ=vlm时
此时梯度为xl∑i≠lvimxi.
综合上述结论,f(x)关于θ的偏导数为:
1.2.6 训练时间复杂度
由上述式(15)可以得到:
对于上式中的前半部分∑ni=1vimxi,对于每个样本只需要计算一次,所以时间复杂度为O(n),对于k个隐变量的维度分别计算一次,则复杂度为O(kn)。其它项的时间复杂度都小于这一项,因此,模型训练的时间复杂度为O(kn)。
详细一点解释:
(1)我们首先计算∑ni=1vimxi
,时间复杂度为n,这个值对于所有特征对应的隐变量的某一个维度是相同的。我们设这值为C。
(2)计算每一个特征对应的xl∑ni=1vimxi−vlmx2l=Cxl−vlmx2l,由于总共有n个特征,因此时间复杂度为n,至此,总的时间复杂度为n+n。
(3)上述只是计算了隐变量的其中一个维度,我们总共有k个维度,因此总的时间复杂度为k(n+n)=O(kn).
2、FFM
2.1 背景及基本原理
在FM模型中,每一个特征会对应一个隐变量,但在FFM模型中,认为应该将特征分为多个field,每个特征对应每个field分别有一个隐变量。
举个例子,我们的样本有3种类型的字段:publisher, advertiser,
gender,分别可以代表媒体,广告主或者是具体的商品,性别。其中publisher有5种数据,advertiser有10种数据,gender有男女2种,经过one-hot编码以后,每个样本有17个特征,其中只有3个特征非空。
如果使用FM模型,则17个特征,每个特征对应一个隐变量。
如果使用FFM模型,则17个特征,每个特征对应3个隐变量,即每个类型对应一个隐变量,具体而言,就是对应publisher, advertiser, gender三个field各有一个隐变量。
2.2模型与最优化问题
2.2.1 模型
根据上面的描述,可以得出FFM的模型为:
其中j1,j2表示特征的索引。我们假设j1特征属于f1这个field,j2特征属于f2这个field,则Vj1,f2表示j1这个特征对应f2(j2所属的field)的隐变量,同时Vj2,f1表示j2这个特征对应f1(j1所属的field)的隐变量。
事实上,在大多数情况下,FFM模型只保留了二次项,即:
2.2.2 最优化问题
根据逻辑回归的损失函数及分析,可以得出FFM的最优化问题为:
上面加号的前面部分使用了L2范式,后面部分是逻辑回归的损失函数。m表示样本的数量,yi表示训练样本的真实值(如是否点击的-1/1),ϕ(V,x)表示使用当前的V代入式(18)计算得到的值。
注意,以上的损失函数适用于样本分布为{-1,1}的情况。
2.2.3 自适应学习率
与FTRL一样,FFM也使用了累积梯度作为学习率的一部分,即:
其中gvj1,f2表示对于Vj1,f2这个变量的梯度向量,因为Vj1,f2是一个向量,因此gvj1,f2也是一个向量,尺寸为隐变量的维度大小,即k。
而∑t(gtvj1,f2)2表示从第一个样本到当前样本一直以来的累积梯度平方和。
2.2.4 FFM算法的最终形式
其中G为累积梯度平方:
g为梯度,比如gj1,f2为j1这个特征对应f2这个field的梯度向量:
原文参考:https://blog.csdn.net/jediael_lu/article/details/77772565