python-opencv实现一种基于图像边缘梯度的边缘模板匹配

1、介绍

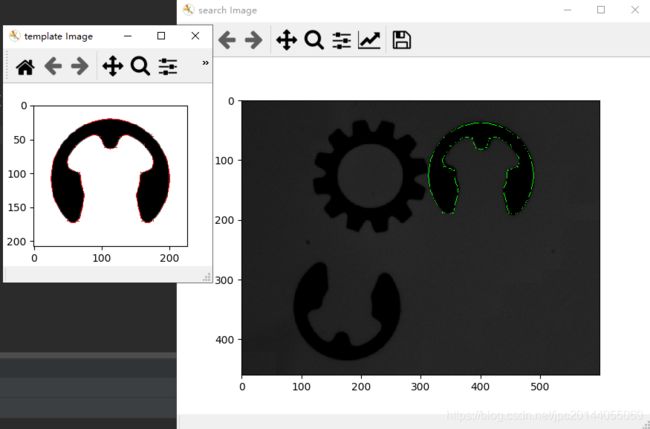
模板匹配是一个当被搜索图像中对象的姿态 $(X,Y,\theta )$ 未知时，使用模板图像去匹配对象的图像处理方法。在这里实现的是利用目标的边缘信息来识别搜索图像中的目标。

2、背景

模板匹配由于它的速度和可靠性问题，在本质上是一个棘手的问题。当物体是部分可见或者混合其他对象时，解决方法应该对亮度变化具有鲁棒性，更重要的是，算法应该具有计算效率。解决这一问题的方法主要有基于灰度值的匹配（或基于区域匹配）和基于特征的匹配（非基于区域的匹配）。OpenCV中自带的模板匹配，完全是基于像素的模板匹配，很容易受光照的影响。

• 基于灰度值的方法:

在基于灰度值的匹配中，归一化互相关(Normalized Cross Correlation，NCC)算法由来已久。这通常是通过每一步减去均值然后除以标准差来完成的。模板$t(x,y)$ 与子图像 $f(x,y)$ 的互相关为:
$$NCC=\frac{1}{n-1}\sum _{x,y}\frac{(f(x,y)-\mu f)(t(x,y)-\mu t)}{\sigma f.\sigma t}$$
其中，$n$ 是$t(x,y)$ 和 $f(x,y)$ 中的像素个数。

虽然这个方法对于现行光照具有较强的鲁棒性，但是当对象部分可见或与其他对象混合时，算法就是失效。此外，该方法需要计算模板图像中所有像素与搜索图像之间的相关性，因此计算成本较高。

• 基于特征的方法:

基于特征的模板匹配方法在图像处理领域得到了广泛的应用。就像基于边缘的对象识别，其中对象边缘是匹配的特征，在广义霍夫变换中，将使用对象的几何特征进行匹配。

这里实现了一种算法，该算法使用对象的边缘信息来识别搜索图像的对象。这个实现使用OpenCV( the Open-Source Computer Vision library)作为平台。

3、算法

解释一个基于边缘的模板匹配技术。边缘可以定义为数字图像中亮度急剧变化或存在不连续的点。从技术上讲，它是一个离散的微分运算，计算出图像强度函数的梯度近似值。

边缘检测的方法有很多种，但大多可以分为基于搜索和基于零交叉两大类。基于搜索的边缘检测方法首先计算边缘强度，通常是梯度大小等一阶导数表达式，然后通过计算边缘的局部方向估计(通常是梯度方向)来寻找梯度大小的局部方向最大值。这里我们使用的是Sobel实现的边缘检测方法。这种操作是计算每个点的图像强度梯度，给出从亮到暗的最大可能增加的方法和该方法的变化率。

我们用$X$方向和$Y$方向上的梯度或导数来匹配。

这个算法包括两个步骤。首先，我们需要创建一个基于模板图像模型，然后使用这个模型在搜索图像中进行搜索。

(1)、创建基于边缘的模板模型

我们首先从模板图像的边缘创建一个数据集或模板模型，用于在搜索图像中查找该对象的姿态。这里我们使用了一种变异的Canny边缘检测方法来找到边缘。对于边缘提取，Canny使用以下步骤:

• Step 1： 查找图像的强度梯度

对模板图像使用Sobel滤波器，它在$X(G_x)$ 和 $Y(G_y)$ 方向上返回梯度。从这个梯度上，我们将使用以下公式返回边缘大小和方向
$$Magnitude=\sqrt{G_x^2+G_y^2}$$
$$Direction=invtan(\frac{G_x}{G_y})$$

我们使用OpenCV函数来查找这些值。

gx = cv2.Sobel(src, cv2.CV_32F, 1, 0, 3)
gy = cv2.Sobel(src, cv2.CV_32F, 0, 1, 3)

for i in range(1, Ssize[1]-1):
    for j in range(1, Ssize[0]-1):
        fdx = gx[i][j]  # 读x, y的导数值
        fdy = gy[i][j]

        MagG = (float(fdx*fdx) + float(fdy * fdy))**(1/2.0)  # Magnitude = Sqrt(gx^2 +gy^2)
        direction = cv2.fastAtan2(float(fdy), float(fdx))  # Direction = invtan (Gy / Gx)
        magMat[i][j] = MagG

        if MagG > MaxGradient:
            MaxGradient = MagG  # 获得最大梯度值进行归一化。

        # 从0,45,90,135得到最近的角
        if (direction > 0 and direction < 22.5) or (direction > 157.5 and direction < 202.5) or (direction > 337.5 and direction < 360):
            direction = 0
        elif (direction > 22.5 and direction < 67.5) or (direction >202.5 and direction <247.5):
            direction = 45
        elif (direction >67.5 and direction < 112.5) or (direction>247.5 and direction<292.5):
            direction = 90
        elif (direction >112.5 and direction < 157.5) or (direction>292.5 and direction<337.5):
            direction = 135
        else:
            direction = 0

        orients.append(int(direction))

一旦找到边缘方向，下一步就是关联图像中可以跟踪的边缘方向。有四个可能的方向来描述周围的像素:0度、45度、90度和135度。我们把所有的方向都分配给这些角。

• Step 2： 查找图像的强度梯度

在找到边缘方向后，我们将做一个非最大抑制算法。非最大抑制沿边缘方向跟踪左、右像素，当当前像素大小小于左、右像素大小时则抑制当前像素大小。这将导致一个薄的图像。

for i in range(1, Ssize[1]-1):
    for j in range(1, Ssize[0] - 1):
        if orients[count] == 0:
            leftPixel = magMat[i][j- 1]
            rightPixel = magMat[i][j+1]
        elif orients[count] == 45:
            leftPixel = magMat[i - 1][j + 1]
            rightPixel = magMat[i+1][j - 1]
        elif orients[count] == 90:
            leftPixel = magMat[i - 1][j]
            rightPixel = magMat[i+1][j]
        elif orients[count] == 135:
            leftPixel = magMat[i - 1][j-1]
            rightPixel = magMat[i+1][j+1]

        if (magMat[i][j] < leftPixel) or (magMat[i][j] < rightPixel):
            nmsEdges[i][j] = 0
        else:
            nmsEdges[i][j] = int(magMat[i][j]/MaxGradient*255)
        count = count + 1

• Step 3： 做滞后阈值

使用滞后阈值需要两个阈值:高阈值和低阈值。我们应用一个高阈值来标记那些我们可以相当肯定是真品的边缘。从这些开始，使用前面得到的方向信息，可以通过图像跟踪其他边缘。在跟踪边缘时，我们应用较低的阈值，只要找到一个起始点，就可以跟踪边缘的模糊部分。

RSum = 0
CSum = 0
flag = 1
# 做滞后阈值
for i in range(1, Ssize[1]-1):
    for j in range(1, Ssize[0]-1):
        fdx = gx[i][j]
        fdy = gy[i][j]
        MagG = (fdx*fdx + fdy*fdy)**(1/2)   # Magnitude = Sqrt(gx^2 +gy^2)
        DirG = cv2.fastAtan2(float(fdy), float(fdx))  # Direction = tan(y/x)

        flag = 1
        if float(nmsEdges[i][j]) < maxContrast:
            if float(nmsEdges[i][j]) < minContrast:
                nmsEdges[i][j] = 0
                flag = 0
            else: # 如果8个相邻像素中的任何一个不大于maxContrast，则从边缘删除
                if float(nmsEdges[i-1][j-1]) < maxContrast and \
                    float(nmsEdges[i-1][j]) < maxContrast and \
                    float(nmsEdges[i-1][j+1]) < maxContrast and \
                    float(nmsEdges[i][j-1]) < maxContrast and \
                    float(nmsEdges[i][j+1]) < maxContrast and \
                    float(nmsEdges[i+1][j-1]) < maxContrast and \
                    float(nmsEdges[i+1][j]) < maxContrast and \
                    float(nmsEdges[i+1][j+1]) < maxContrast:
                    nmsEdges[i][j] = 0
                    flag = 0

• Step 4： 保存数据集

提取出边后，将所选边的X、Y导数以及坐标信息保存为模板模型。这些坐标将被重新排列，以反映作为重心的起始点。

(2)、找到基于边缘的模板模型

算法的下一个任务是使用模板模型在搜索图像中找到目标。我们可以看到我们从包含一组点$p_i^T=(X_i^T,Y_i^T)$ 的模板映像创建的模型和它的在X和Y方向上的梯度$G_i^T=(G_{xi}^T,G_{yi}^T)$, 其中$i=1...n,n$是模板(T)数据集中元素的数量。

我们还可以在搜索图像（S）中找到梯度$G_{u,v}^S=(G{x}_{u,v}^S,G{y}_{u,v}^S)$, 其中$u=1...rows$(搜索图像的高)，$v=1...cols$(搜索图像的宽)。

在匹配过程中，模板模型应使用相似性度量与搜索图像在所有位置进行比较。相似度度量的思想是取模板图像梯度向量的所有归一化点积的和，并在模型数据集中的所有点上搜索图像。这将在搜索图像的每个点上得到一个分数。其公式如下:
$$S_{u,v}=\frac{1}{n}\sum _{i=1}^n\frac{(G{x}_i^T.{Gx}_{(u+X_i,v+Y_i)}^S)+(G{y}_i^T.{Gy}_{(u+X_i,v+Y_i)}^S)}{\sqrt{G{x}_i^{T^2}+G{y}_i^{T^2}}.\sqrt{{{Gx}_{(u+Xi,v+Yi)}^T}^2+{{Gy}_{(u+Xi,v+Yi)}^T}^2}}$$

如果模板模型和搜索图像完全匹配，这个函数将返回1。该分数对应于搜索图像中可见对象的部分。如果该对象不在搜索图像中，则得分为0。

Sdx = cv2.Sobel(src, cv2.CV_32F, 1, 0, 3)  # 找到X导数
Sdy = cv2.Sobel(src, cv2.CV_32F, 0, 1, 3)  # 找到Y导数

for i in range(0, height):
    for j in range(0, wight):
        partialSum = 0  # 初始化partialSum
        for m in range(0, Nof):
            curX = i + self.cordinates[m][0]  # 模板X坐标
            curY = j + self.cordinates[m][1]  # 模板Y坐标
            iTx = self.edgeDerivativeX[m]  # 模板X的导数
            iTy = self.edgeDerivativeY[m]  # 模板Y的导数

            if curX < 0 or curY < 0 or curX > Ssize[1] - 1 or curY > Ssize[0] - 1:
                continue

            iSx = Sdx[curX][curY]  # 从源图像得到相应的X导数
            iSy = Sdy[curX][curY]  # 从源图像得到相应的Y导数

            if (iSx != 0 or iSy != 0) and (iTx != 0 or iTy != 0):
                # //partial Sum  = Sum of(((Source X derivative* Template X drivative) + Source Y derivative * Template Y derivative)) / Edge magnitude of(Template)* edge magnitude of(Source))
                partialSum = partialSum + ((iSx*iTx)+(iSy*iTy))*(self.edgeMagnitude[m] * matGradMag[curX][curY])

在实际情况下，我们需要加快搜索过程。这可以通过各种方法来实现。第一种方法是利用平均的性质。在寻找相似度度量时，如果我们可以为相似度度量设置一个最小值 $(S^{min})$ ，那么我们就不需要对模板模型中的所有点进行评估。为了检验在特定点$J$ 处的部分分数$S_{uv}$ ，我们需要找到部分和$Sm$。点$m$处的$Sm$可定义为:

$$S{m}_{(u,v)}=\frac{1}{m}\sum _{i=1}^m\frac{(G{x}_i^T.G{x}_{(u+Xi,v+Yi)}^S)+(G{y}_i^T.G{y}_{(u+Xi,v+Yi)}^S)}{\sqrt{G{x}_i^{T^2}+G{y}_i^{T^2}}.\sqrt{{G{x}_{(u+Xi,v+Yi)}^T}^2+{G{y}_{(u+Xi,v+Yi)}^T}^2}}$$

显然，和的其余项都小于或等于1。因此如果$S_m>S^{min}-1+m/n$，我们可以停止评估。

另一个标准是，任何点的部分分数都应该大于最小值，即$Sm\ge S^{min}m/n$,当使用此条件时，匹配将非常快。但问题是，如果首先检查对象的缺失部分，那么部分和就会很低。在这种情况下，对象的实例将不被视为匹配。我们可以用另一个标准来修改它，我们用一个安全的停止标准来检查模板模型的第一部分，用一个硬标准来检查剩下的部分$S^{min}m/n$。用户可以指定一个贪婪参数$greediness(g)$，其中使用硬标准检查模板模型的分数。因此，如果g=1，则用硬标准检查模板模型中的所有点，如果g=0，所有的点都将只使用安全标准进行检查。我们可以把这个过程写成如下形式。

部分分数的评定可停在:
$$S_m<MIN((S^{min}-1+\frac{1-g.S^{min}}{1-g}.\frac{m}{n}),(S_{min}.\frac{m}{n}))$$

normMinScore = minScore/ self.noOfCordinates  # 预计算minScore
normGreediness = ((1- greediness*minScore)/(1-greediness)) / self.noOfCordinates  # 预计算greediness

sumOfCoords = m+1
partialScore = partialSum/sumOfCoords
# 检查终止条件
# 如果部分得分小于该位置所需的得分
# 在那个坐标中断serching。
if partialScore < min((minScore - 1) + normGreediness*sumOfCoords, normMinScore*sumOfCoords):
    break

这种相似性度量有以下几个优点：由于所有梯度向量都是归一化的，所以相似性测度对非线性光照变化是不变的。由于没有对边缘滤波进行分割，因此在光照变化时，边缘滤波能显示出真实的不变性。更重要的是，当对象部分可见或与其他对象混合时，这种相似性度量是可靠的。

（3）增强

此算法可能有各种增强。为了进一步加速搜索过程，可以使用金字塔方法。在本例中，搜索以低分辨率和小图像大小开始。这相当于金字塔的顶端。如果搜索在此阶段成功，搜索将继续到金字塔的下一层，即更高分辨率的图像。以这种方式，搜索继续，因此，结果是细化，直到原始图像的大小，即。到达金字塔的底部。

---

参考：https://www.codeproject.com/articles/99457/edge-based-template-matching
完整版的python-opencv模板匹配算法见下面链接