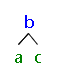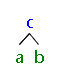数据结构编程练习（二叉树）

1.基于二叉链表的二叉树的遍历

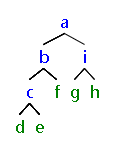
描述：设二叉树中每个结点的元素均为一个字符，按先序遍历的顺序建立二叉链表，编写三个递归算法分别实现二叉树的先序、中序和后序遍历。

输入样例：
abcd00e00f00ig00h00
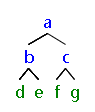
abd00e00cf00g00
0

输出样例：
abcdefigh
dcebfagih
decfbghia
abdecfg
dbeafcg
debfgca

#include 
#include 

#define MAX_SIZE 100

typedef struct BiTNode {
    char data;
    struct BiTNode *left, *right;
} BiTNode, *BiTree;

void BiTree_create(BiTree *T, char *node_data, int *cursor);

void pre_order_traverse(BiTree T);

void in_order_traverse(BiTree T);

void post_order_traverse(BiTree T);

void BiTree_free(BiTree T);

int main() {
    char str[MAX_SIZE];

    while (scanf("%s", str) && str[0] != 48) {
        int i = 0;
        BiTree T = NULL;

        BiTree_create(&T, str, &i);

        printf("\n");
        pre_order_traverse(T);//trəˈvɜːs
        printf("\n");
        in_order_traverse(T);
        printf("\n");
        post_order_traverse(T);

        BiTree_free(T);
    }

    return 0;
}

void BiTree_create(BiTree *T, char *node_data, int *cursor) {
    if (node_data[*cursor] == 48) {
        *T = NULL;
    } else {
        *T = (BiTree) malloc(sizeof(BiTNode));
        (*T)->data = node_data[*cursor];

        (*cursor)++;
        BiTree_create(&((*T)->left), node_data, cursor);
        (*cursor)++;
        BiTree_create(&((*T)->right), node_data, cursor);
    }
}

void pre_order_traverse(BiTree T) {
    if (T) {
        printf("%c", T->data);
        pre_order_traverse(T->left);
        pre_order_traverse(T->right);
    }
}

void in_order_traverse(BiTree T) {
    if (T) {
        in_order_traverse(T->left);
        printf("%c", T->data);
        in_order_traverse(T->right);
    }
}

void post_order_traverse(BiTree T) {
    if (T) {
        post_order_traverse(T->left);
        post_order_traverse(T->right);
        printf("%c", T->data);
    }
}

void BiTree_free(BiTree T) {
    if (T) {
        BiTree_free(T->left);
        BiTree_free(T->right);
        free(T);
    }
}

2.基于二叉链表的二叉树高度的计算

描述：设二叉树中每个结点的元素均为一个字节，按先序遍历的顺序建立二叉链表，编写递归算法计算二叉树的高度。

输入样例：
abcd00e00f00ig00h00
abd00e00cf00g00
0

输出样例：
4
3

#include 
#include 

#define MAX_SIZE 100

typedef struct BiTNode {
    char data;
    struct BiTNode *left, *right;
} BiTNode, *BiTree;

void BiTree_create(BiTree *T, char *node_data, int *cursor);

void BiTree_free(BiTree T);

int BiTree_height(BiTree T);

void BiTree_depth(BiTree T, int now_depth, int *max_depth);

int main() {
    char str[MAX_SIZE];

    while (scanf("%s", str) && str[0] != 48) {
        BiTree T;
        int i = 0;

        BiTree_create(&T, str, &i);

        /*recursion with return value*/
        printf("\n%d", BiTree_height(T));

        /*recursion without return value*/
        /*int depth = 0;
        BiTree_depth(T, 1, &depth);
        printf("\n%d", depth);*/

        BiTree_free(T);
    }

    return 0;
}

void BiTree_create(BiTree *T, char *node_data, int *cursor) {
    if (node_data[*cursor] == 48) {
        *T = NULL;
    } else {
        *T = (BiTree) malloc(sizeof(BiTNode));
        (*T)->data = node_data[*cursor];

        (*cursor)++;
        BiTree_create(&((*T)->left), node_data, cursor);
        (*cursor)++;
        BiTree_create(&((*T)->right), node_data, cursor);
    }
}

void BiTree_free(BiTree T) {
    if (T) {
        BiTree_free(T->left);
        BiTree_free(T->right);
        free(T);
    }
}
/**
 * calculate height by return value
 * @param T current root node
 * @return height of current node
 */
int BiTree_height(BiTree T) {
    if (T) {
        int l_height = BiTree_height(T->left) + 1;
        int r_height = BiTree_height(T->right) + 1;
        return (l_height > r_height) ? l_height : r_height;
    }
    return 0;
}
/**
 * calculate depth with parameter
 * @param T current root node
 * @param now_depth depth of current node
 * @param max_depth depth of this tree
 */
void BiTree_depth(BiTree T, int now_depth, int *max_depth) {
    if (T) {
        if (now_depth > *max_depth) {
            *max_depth = now_depth;
        }
        BiTree_depth(T->left, now_depth + 1, max_depth);
        BiTree_depth(T->right, now_depth + 1, max_depth);
    }
}

3.基于二叉链表的二叉树结点个数的统计

描述：设二叉树中每个结点的元素均为一个字符，按先序遍历的顺序建立二叉链表，编写三个递归算法对二叉树的结点（度为0、1、2）个数进行统计。

输入样例：
abcd00e00f00ig00h00
abd00e00cf00g00
0

输出样例：
5 0 4
4 0 3

#include 
#include 

#define MAX_SIZE 100

typedef struct BiTNode {
    char data;
    struct BiTNode *left, *right;
} BiTNode, *BiTree;

void BiTree_create(BiTree *T, char *node_data, int *cursor);

void BiTree_free(BiTree T);

void post_order_count(BiTree T, int *degree);

int main() {
    char str[MAX_SIZE];
    while (scanf("%s", str) && str[0] != 48) {
        BiTree T;
        int i = 0;
        int degree[3] = {0, 0, 0};

        BiTree_create(&T, str, &i);
        post_order_count(T, degree);
        printf("%c%d%c%d%c%d", 10, degree[0], 32, degree[1], 32, degree[2]);
        BiTree_free(T);
    }

    return 0;
}

void BiTree_create(BiTree *T, char *node_data, int *cursor) {
    if (node_data[*cursor] == 48) {
        *T = NULL;
    } else {
        *T = (BiTree) malloc(sizeof(BiTNode));
        (*T)->data = node_data[*cursor];

        (*cursor)++;
        BiTree_create(&((*T)->left), node_data, cursor);
        (*cursor)++;
        BiTree_create(&((*T)->right), node_data, cursor);
    }
}

void BiTree_free(BiTree T) {
    if (T) {
        BiTree_free(T->left);
        BiTree_free(T->right);
        free(T);
    }
}

void post_order_count(BiTree T, int *degree) {
    if (T) {
        post_order_count(T->left, degree);
        post_order_count(T->right, degree);
        if (T->left == NULL) {
            if (T->right == NULL) {
                degree[0]++;
            } else {
                degree[1]++;
            }
        } else {
            if (T->right == NULL) {
                degree[1]++;
            } else {
                degree[2]++;
            }
        }
    }
}

4.基于二叉链表的二叉树左右孩子的交换

描述：设二叉树中每个结点的元素均为一个字符，按先序遍历的顺序建立二叉链表，编写递归算法交换该二叉树的左右孩子。

输入样例：
abcd00e00f00ig00h00
abd00e00cf00g00
0

输出样例：
aihgbfced
acgfbed

#include 
#include 

#define MAX_SIZE 100

typedef struct BiTNode {
    char data;
    struct BiTNode *left, *right;
} BiTNode, *BiTree;

void BiTree_create(BiTree *T, char *node_data, int *cursor);

void BiTree_free(BiTree T);

void BiTree_mirror(BiTree T);

void pre_order_traverse(BiTree T);

int main() {
    char str[MAX_SIZE];
    while (scanf("%s", str) && str[0] != 48) {
        BiTree T;
        int i = 0;

        BiTree_create(&T, str, &i);
        BiTree_mirror(T);
        printf("\n");
        pre_order_traverse(T);
        BiTree_free(T);
    }

    return 0;
}

void BiTree_create(BiTree *T, char *node_data, int *cursor) {
    if (node_data[*cursor] == 48) {
        *T = NULL;
    } else {
        *T = (BiTree) malloc(sizeof(BiTNode));
        (*T)->data = node_data[*cursor];

        (*cursor)++;
        BiTree_create(&((*T)->left), node_data, cursor);
        (*cursor)++;
        BiTree_create(&((*T)->right), node_data, cursor);
    }
}

void BiTree_free(BiTree T) {
    if (T) {
        BiTree_free(T->left);
        BiTree_free(T->right);
        free(T);
    }
}

void BiTree_mirror(BiTree T) {
    if (T) {
        BiTree_mirror(T->left);
        BiTree_mirror(T->right);

        BiTNode *tmp = T->left;
        T->left = T->right;
        T->right = tmp;
    }
}

void pre_order_traverse(BiTree T) {
    if (T) {
        printf("%c", T->data);
        pre_order_traverse(T->left);
        pre_order_traverse(T->right);
    }
}

5.二叉排序树的判定

描述：假设二叉树每个结点的元素均为一个单字符，根据给定的字符序列按照先序遍历的顺序递归创建该树的二叉链表，然后判断该二叉树是否为二叉排序树。

输入样例：
ba##c##
ca##b##
#

输出样例：
YES
NO

#include 
#include 
#include 

#define MAX_SIZE 100

typedef struct BiTNode {
    char data;
    struct BiTNode *left, *right;
} BiTNode, *BiTree;

void BiTree_create(BiTree *T, char *node_data, int *cursor);

void BiTree_free(BiTree T);

bool is_BST(BiTree T, int last_value);

int main() {
    char str[MAX_SIZE];
    while (scanf("%s", str) && str[0] != 35) {
        BiTree T;
        int i = 0;

        BiTree_create(&T, str, &i);
        if (is_BST(T, INT_MIN)) {
            printf("\nYES");
        } else {
            printf("\nNO");
        }
        BiTree_free(T);
    }

    return 0;
}

void BiTree_create(BiTree *T, char *node_data, int *cursor) {
    if (node_data[*cursor] == 35) {
        *T = NULL;
    } else {
        *T = (BiTree) malloc(sizeof(BiTNode));
        (*T)->data = node_data[*cursor];

        (*cursor)++;
        BiTree_create(&((*T)->left), node_data, cursor);
        (*cursor)++;
        BiTree_create(&((*T)->right), node_data, cursor);
    }
}

void BiTree_free(BiTree T) {
    if (T) {
        BiTree_free(T->left);
        BiTree_free(T->right);
        free(T);
    }
}
/**
 * judge whether the middle sequence is an increasing sequence
 * @param T current root node
 * @param last_value the value of the last visited node
 * @return whether tree T is a BST
 */
bool is_BST(BiTree T, int last_value) {
    if (T) {
        /*judge left subtree*/
        if (!is_BST(T->left, last_value))
            return false;
        /*judge middle order sequence*/
        if (T->data <= last_value)
            return false;
        last_value = T->data;
        /*judge right subtree*/
        if (!is_BST(T->right, last_value))
            return false;
    }
    return true;
}

/**
 * according to the definition of BST
 * @param T current root node
 * @return whether tree T is a BST
 */
bool is_BST(BiTree T) {
    if (T) {
        if (!is_BST(T->left))
            return false;
        if (!is_BST(T->right))
            return false;
        if (!(left_subtree_max_value(T) < T->data && T->data < right_subtree_min_value(T)))
            return false;
    }
    return true;
}

int right_subtree_min_value(BiTree T) {
    if (T->right == NULL) {
        return INT_MAX;
    }
    T = T->right;
    while (T->left != NULL) {
        T = T->left;
    }
    return T->data;
}

int left_subtree_max_value(BiTree T) {
    if (T->left == NULL) {
        return INT_MIN;
    }
    T = T->left;
    while (T->right != NULL) {
        T = T->right;
    }
    return T->data;
}