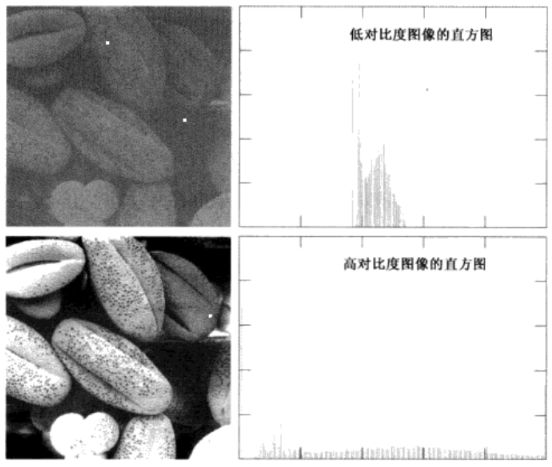
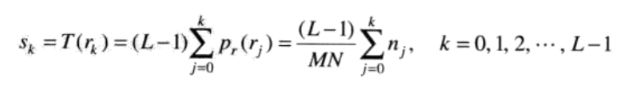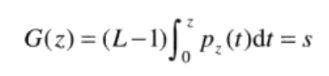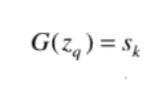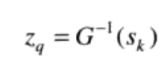灰度直方图是图像中像素灰度集的一种统计反应。它能够描述图像中灰度的分布情况，直观地展现出图像中灰度所占多少。直方图横轴表示像素的灰度范围（比如说 0~255），纵轴表示的是像素的数量或者密度。亮暗、对比度、图像中的内容不同，直方图的表现也会不同。本文主要参考《冈萨雷斯》一书。
灰度直方图
1.直方图均衡
有的图像的灰度分布不均匀，出现过亮过暗，或者对比度过低的情况，这样的图像细节不明显，在肉眼观察时会丢失一些信息。这时可以使用直方图均衡技术对图像进行变换，变成肉眼易于分辨的细节分明的图像。
直方图均衡的目标
要对直方图进行均衡，首先要通过统计得到原图像的直方图，然后通过下面这个神奇的公式，对灰度值进行变换。其中 r 是输入像素的灰度，函数 T 表示一种变换，s 是输出像素的灰度，pr 是原图像灰度的PDF（概率密度函数）。至于这个公式怎么来的，《冈萨雷斯》一书上貌似并没有讲清楚，但其实可以通过直觉来理解。
直方图均衡公式
图像是离散的，所以实际中使用的是离散形式
离散形式
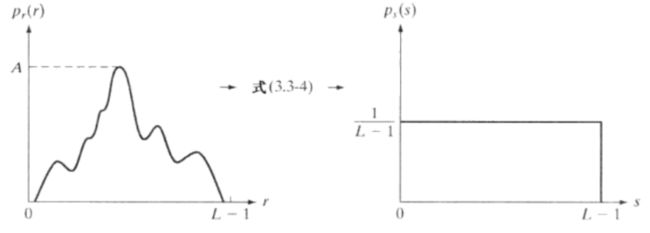
那么使用上面的公式，就可以将直方图变换成这个样子，这样的图像一般具有比较好的细节表现。
ps是输出图像的PDF（其实也可以理解为直方图）
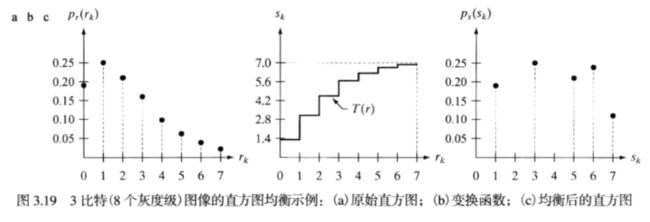
举个书上的栗子就很好理解了
2.直方图匹配（规定化）
一般来说，直方图均衡能够自动地确定变换函数，且输出结果比较好，当时需要自动增强时是一种好方法。但有的情况下，使用直方图均衡并不是最好的办法。有时候我们可以指定特定的直方图，而不是均匀分布的直方图，并让原图像的直方图变换成我们指定的形式。这个过程称为直方图匹配或者直方图规定化。
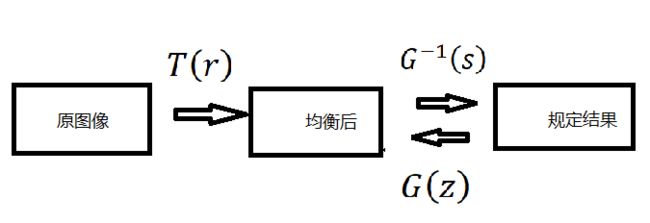
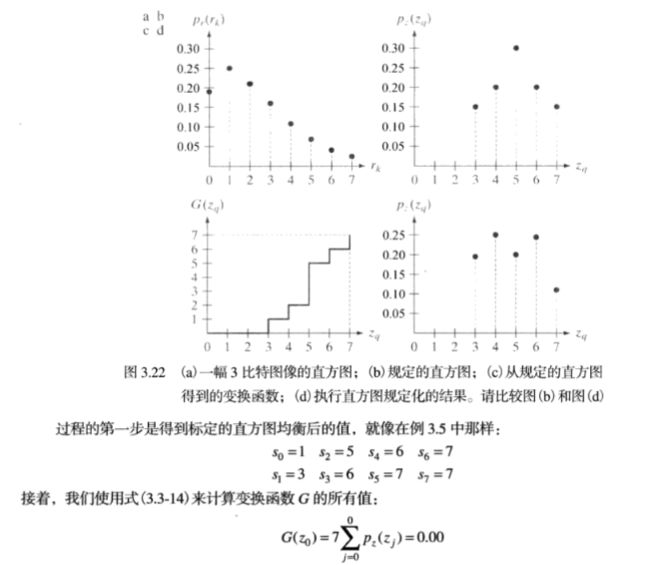
在推导过程中，直方图规定化的过程如下：
1.对原图像进行直方图均衡。和上面一样。
直方图均衡公式
2.对事先规定的直方图也进行均衡。z为最终输出图像像素的灰度值。
均衡的结果跟原图像的直方图均衡的结果是一样的
3.那么从数学上可以得到反变换函数。对均衡后的图像进行反变换就可以得到直方图规定化的结果了。
反变换
我这里做个图解释一下
r s z 分别代表输入图像，均衡图像和规定化图像的像素灰度
同样的，写成离散形式。
对规定直方图进行均衡
对应关系
反变换
同样的，上例子
3.代码实现
感觉OpenCV在直方图处理这方面并不怎么走心。这里使用的是另一篇博客的类封装和算法实现。
直方图规定化中要注意两点：
实际操作中不会进行两次均衡化。在推导中发现，假如sk 规定化后的对应灰度是zm的话，需要满足的条件是sk的累积概率和zm的累积概率是最接近的。所以可以根据计算累计密度的差值来进行映射。
手动输入一个直方图比较困难，这里使用一个参考图像来进行实现。参考图像的直方图就是我们指定的直方图。
/********************************************************************
* Created by 杨帮杰 on 11/10/18
* Right to use this code in any way you want without
* warranty, support or any guarantee of it working
* E-mail: [email protected]
* Association: SCAU 华南农业大学
********************************************************************/
#include
#include
#include
#include
#include
#include
#include
#include
#define IMAGE1_PATH "/home/jacob/图片/1.png"
#define IMAGE2_PATH "/home/jacob/图片/2.png"
#define IMAGE3_PATH "/home/jacob/图片/3.png"
using namespace std;
using namespace cv;
class Histogram1D
{
private:
int histSize[1]; // 项的数量
float hranges[2]; // 统计像素的最大值和最小值
const float* ranges[1];
int channels[1]; // 仅计算一个通道
public:
Histogram1D()
{
// 准备1D直方图的参数
histSize[0] = 256;
hranges[0] = 0.0f;
hranges[1] = 255.0f;
ranges[0] = hranges;
channels[0] = 0;
}
Mat getHistogram(const Mat &image)
{
Mat hist;
// 计算直方图
calcHist(&image ,// 要计算图像的
1, // 只计算一幅图像的直方图
channels, // 通道数量
Mat(), // 不使用掩码
hist, // 存放直方图
1, // 1D直方图
histSize, // 统计的灰度的个数
ranges); // 灰度值的范围
return hist;
}
Mat getHistogramImage(const Mat &image)
{
Mat hist = getHistogram(image);
//查找最大值用于归一化
double maxVal = 0;
minMaxLoc(hist, NULL, &maxVal);
//绘制直方图的图像
Mat histImg(histSize[0], histSize[0], CV_8U, Scalar(255));
// 设置最高点为最大值的90%
double hpt = 0.9 * histSize[0];
//每个条目绘制一条垂直线
for (int h = 0; h < histSize[0]; h++)
{
//直方图的元素类型为32位浮点数
float binVal = hist.at(h);
int intensity = static_cast(binVal * hpt / maxVal);
line(histImg, Point(h, histSize[0]),
Point(h, histSize[0] - intensity), Scalar::all(0));
}
return histImg;
}
};
/**
* @brief EqualizeImage 对灰度图像进行直方图均衡化
* @param src 输入图像
* @param dst 均衡化后的图像
*/
void EqualizeImage(const Mat &src, Mat &dst)
{
Histogram1D hist1D;
Mat hist = hist1D.getHistogram(src);
hist /= (src.rows * src.cols); // 对得到的灰度直方图进行归一化,得到密度（0～1）
float cdf[256] = {0}; // 灰度的累积概率
Mat lut(1, 256, CV_8U); // 创建用于灰度变换的查找表
for (int i = 0; i < 256; i++)
{
// 计算灰度级的累积概率
if (i == 0)
cdf[i] = hist.at(i);
else
cdf[i] = cdf[i - 1] + hist.at(i);
lut.at(i) = static_cast(255 * cdf[i]); // 创建灰度的查找表
}
LUT(src, lut, dst); // 应用查找表，进行灰度变化，得到均衡化后的图像
}
/**
* @brief HistSpecify 对灰度图像进行直方图规定化
* @param src 输入图像
* @param ref 参考图像，解析参考图像的直方图并用于规定化
* @param result 直方图规定化后的图像
* @note 手动设置一个直方图并用于规定化比较麻烦，这里使用一个参考图像来进行
*/
void HistSpecify(const Mat &src, const Mat &ref, Mat &result)
{
Histogram1D hist1D;
Mat src_hist = hist1D.getHistogram(src);
Mat dst_hist = hist1D.getHistogram(ref);
float src_cdf[256] = { 0 };
float dst_cdf[256] = { 0 };
// 直方图进行归一化处理
src_hist /= (src.rows * src.cols);
dst_hist /= (ref.rows * ref.cols);
// 计算原始直方图和规定直方图的累积概率
for (int i = 0; i < 256; i++)
{
if (i == 0)
{
src_cdf[i] = src_hist.at(i);
dst_cdf[i] = dst_hist.at(i);
}
else
{
src_cdf[i] = src_cdf[i - 1] + src_hist.at(i);
dst_cdf[i] = dst_cdf[i - 1] + dst_hist.at(i);
}
}
// 累积概率的差值
float diff_cdf[256][256];
for (int i = 0; i < 256; i++)
for (int j = 0; j < 256; j++)
diff_cdf[i][j] = fabs(src_cdf[i] - dst_cdf[j]);
// 构建灰度级映射表
Mat lut(1, 256, CV_8U);
for (int i = 0; i < 256; i++)
{
// 查找源灰度级为ｉ的映射灰度
// 和ｉ的累积概率差值最小的规定化灰度
float min = diff_cdf[i][0];
int index = 0;
for (int j = 1; j < 256; j++)
{
if (min > diff_cdf[i][j])
{
min = diff_cdf[i][j];
index = j;
}
}
lut.at(i) = static_cast(index);
}
// 应用查找表，做直方图规定化
LUT(src, lut, result);
}
int main()
{
/****************显示图像的直方图******************/
Histogram1D hist1;
Mat img1 = imread(IMAGE1_PATH);
Mat histImg1 = hist1.getHistogramImage(img1);
imshow("Image1", img1);
imshow("Histogram1", histImg1);
/*****************直方图均衡*********************/
Mat equImg = Mat::zeros(img1.rows, img1.cols, img1.type());
EqualizeImage(img1, equImg);
Histogram1D hist2;
Mat histImg2 = hist2.getHistogramImage(equImg);
imshow("Equalized Image1", equImg);
imshow("Histogram2", histImg2);
/*****************直方图规定化*******************/
Mat img2 = imread(IMAGE2_PATH);
Mat img3 = imread(IMAGE3_PATH);
Mat specifyImg = Mat::zeros(img2.rows, img2.cols, img2.type());
HistSpecify(img2, img3, specifyImg);
Histogram1D hist3;
Mat histImg3 = hist3.getHistogramImage(img2);
Histogram1D hist4;
Mat histImg4 = hist4.getHistogramImage(img3);
Histogram1D hist5;
Mat histImg5 = hist5.getHistogramImage(specifyImg);
imshow("Image2", img2);
imshow("Histogram3", histImg3);
imshow("Image3", img3);
imshow("Histogram4", histImg4);
imshow("Specify Image", specifyImg);
imshow("Histogram5", histImg5);
waitKey();
return 0;
}
直方图均衡
原图像和均衡后的直方图
直方图规定化的结果，有一定的误差但效果出来了
原图像直方图、指定的直方图、规定化结果（可能原图欠曝太厉害没办法救了。。）
References:
《数字图像处理》 —— 冈萨雷斯
图像处理基础(8)：图像的灰度直方图、直方图均衡化、直方图规定化（匹配）