【读书笔记】贝叶斯学习

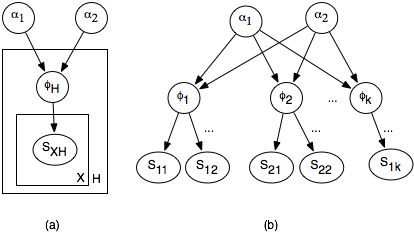
原理

与直接应用贝叶斯公式不同，贝叶斯学习指在当前训练样本的基础上，根据新样本更新每个模型的后验概率。贝叶斯深度学习[1]则结合了神经网络的模型表示能力，将神经网络的权重视作服从某分布的随机变量，而不是固定值；网络的前向传播，就是从权值分布中抽样然后计算。

我们将当前所有样本记为\(\pmb e\)，新样本记为\(X = x\)，待估计的参数或目标标签为\(Y\)，那么学习的目标就是计算后验概率\(P(Y|X=x,\pmb e)\)。在贝叶斯学习中，模型参数具有分布，因此每个标签的输出概率是参数概率（\(P(m|\pmb e)\)，给定新旧样本的后验概率）与对应输出概率\(P(Y|m,x)\)的加权和（其实也是条件概率），具体写为

\[\begin{align} P(Y|X=x,\pmb e) &= \sum_{m\in M}P(Y,m|x,\pmb e)\\ &=\sum_{m\in M}P(Y|m,x,\pmb e)P(m|x,\pmb e)\\ &=\sum_{m\in M}P(Y|m,x)P(m|\pmb e) \end{align} \]

其中最后一步假设了模型已经包含了所有当前样本的信息。由于\(P(Y|m,x)\)是一个已知值，只需用贝叶斯公式计算\(P(m|\pmb e)\)

\[P(m|\pmb e) = \frac{P(\pmb e|m)P(m)}{P(\pmb e)} \]

然而，直接求数据分布\(P(\pmb e)\)是不可能的。处理这个有两种解决思路：

1. 拟合后验分布：用MCMC家族、变分拟合（VI）家族，通过KL散度建立拟合分布与\(P(m|\pmb e)\)后验概率的差异，根据训练样本不断优化得到拟合结果[1]。
2. 省略数据分布：由于分母\(P(\pmb e)\)保证后验概率求和后为1，因此在获得分子的表达式后，可以用一个常数代替其概率值。

例题

考虑单个布尔型随机变量，输出为True的概率为\(\phi\)，为False的概率为\(1-\phi\)，根据不同的样本情况求解\(\phi\)的后验概率。

根据贝叶斯分布，有\(P(\phi|\pmb e) = P(\pmb e|\phi)P(\phi)/P(\pmb e)\)

考虑i.i.d.获取\(n_1\)个True样本，\(n_0\)个False样本，因此其似然函数为

\[P(\pmb e|\phi) = \phi^{n_1}(1-\phi)^{n_0} \]

将未知的先验分布\(P(\phi)\)设为\([0,1]\)上的均匀分布，归一化后可得后验概率如下图

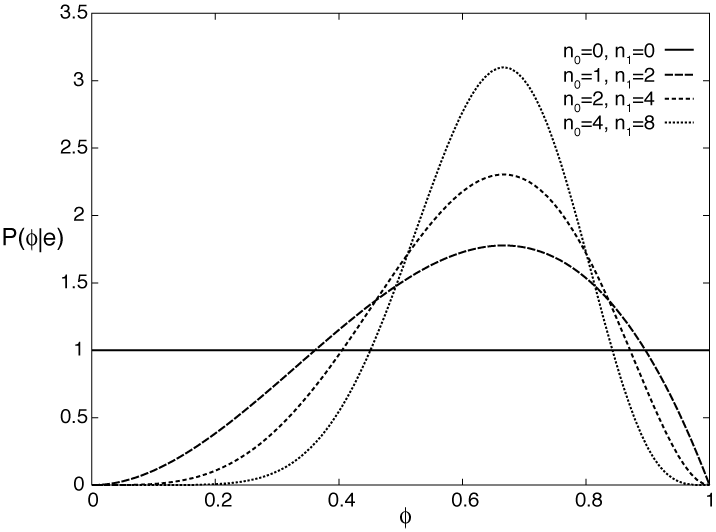
这个先验分布为均匀分布的后验分布又叫做Beta分布，其参数\(\alpha_i=n_i+1\)比样本个数多一，记为

\[Beta^{\alpha_0,\alpha_1}(p)=1/K p^{\alpha_1-1}(1-p)^{\alpha_0-1} \]

同样\(K\)是一个保证积分后为1的归一化系数。有趣的是最大后验概率对应的点在\(\frac{n_1}{n_1+n_0}\)处，而这个分布的期望是\(\frac{n_1+1}{n_1+n_0+2}\)（虽然我觉得期望好像没什么意义）

进一步的，当参数超过2个时，为Dirichlet分布，记为

\[Dirichelet^{\alpha_0,\cdots,\alpha_k}(p_1,\cdots,p_k)=1/K \Pi_{j=1}^k p_j^{\alpha_j-1} \]

其每一维上是一个Beta分布。

优势

1. 当某一类没有样本的时候，直接说\(P(Y=False)=0\)是不正确的，只能说此时为0的后验概率最大，逻辑上是合理的。

2. 对于复杂的相关关系，可以利用贝叶斯网络表明隐变量之间的关系，进行推断。

   

参考链接

[1] C. Blundell, J. Cornebise, K. Kavukcuoglu, and D. Wierstra, “Weight Uncertainty in Neural Networks,” arXiv:1505.05424 [cs, stat], May 2015. [Online]. Available: http://arxiv.org/abs/1505.05424

【读书笔记】贝叶斯原理 - 木坑 - 博客园 (cnblogs.com)