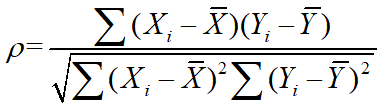Python数据分析与挖掘——线性回归预测模型
线性回归模型属于经典的统计学模型,该模型的应用场景是根据已 知的变量(自变量)来预测某个连续的数值变量(因变量)。例如,餐 厅根据每天的营业数据(包括菜谱价格、就餐人数、预定人数、特价菜 折扣等)预测就餐规模或营业额;网站根据访问的历史数据(包括新用 户的注册量、老用户的活跃度、网页内容的更新频率等)预测用户的支 付转化率;医院根据患者的病历数据(如体检指标、药物服用情况、平 时的饮食习惯等)预测某种疾病发生的概率。
站在数据挖掘的角度看待线性回归模型,它属于一种有监督的学习 算法,即在建模过程中必须同时具备自变量x和因变量y。
相关性分析
一元线性回归模型
一元线性回归模型也被称为简单线性回归模型,是指模型中只含有一个自变量和一个因变量,用来建模的数据集可以表示成{(x1,y1),(x2,y2),……,(xn,yn)}。其中,xi表示自变量x的第i个值,yi表示因变量y的第i个值,n表示数据集的样本量。当模型构建好之后,就可以根据其他自变量x的值,预测因变量y的值,该模型的数学公式可以表示成:
y=a+bx+ε
其中,
a为模型的截距项,
b为模型的斜率项,
ε为模型的误差项。
模型中的a和b统称为回归系数,误差项ε的存在主要是为了平衡等号两边的值,通常被称为模型无法解释的部分。

在上图中,圆点是样本,斜线是一元线性拟合函数。上图反映的就是自变量YearsExperience与因变量Salary之间的散点图,从散点图的趋势来看,工作年限与收入之间存在明显的正相关关系,即工作年限越长,收入水平越高。图中的直线就是关于散点的线性回归拟合线,从图中可知,每个散点基本上都是围绕在拟合线附近。
如果拟合线能够精确地捕捉到每一个点(即所有散点全部落在拟合线上),那么对应的误差项ε应该为0。
所以,模型拟合的越好,则误差项ε应该越小。进而可以理解为:求解参数的问题便是求解误差平方和最小的问题;
拟合线的求解
我们接下来要学会如何根据自变量x和因变量y,求解回归系数a和b。前面已经提到,误差项ε是为了平衡等号两边的值,如果拟合线能够精确地捕捉到每一个点(所有的散点全部落在拟合线上),那么对应的误差项ε应该为0。按照这个思路来看,要想得到理想的拟合线,就必须使误差项ε达到最小。由于误差项是y与a+bx的差,结果可能为正值或负值,因此误差项ε达到最小的问题需转换为误差平方和最小的问题(最小二乘法的思路)。误差平方和的公式可以表示为:
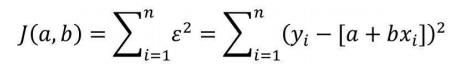
由于建模时的自变量值和因变量值都是已知的,因此求解误差平方和最小值的问题就是求解函数J(a,b)的最小值,而该函数的参数就是回归系数a和b。
该目标函数其实就是一个二元二次函数,如需使得目标函数J(a,b)达到最小,可以使用偏导数的方法求解出参数a和b,进而得到目标函数的最小值。关于目标函数的求导过程如下:



如上推导结果所示,参数a和b的值都是关于自变量x和因变量y的公式。接下来,根据该公式,利用Pyhton计算出回归模型的参数值a和b。

作图
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
#设置绘图风格
plt.style.use('ggplot')
#处理中文乱码
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
#坐标轴负号的处理
plt.rcParams['axes.unicode_minus']=False
#导入数据集
income = pd.read_csv(r'Salary_Data.csv')
#绘制散点图,用seaborn,默认拟合为一元
sns.lmplot(x='YearsExperience', y='Salary', data=income, ci=None)
#设置横纵坐标的刻度范围
plt.xlim((0, 11)) #x轴的刻度范围被设为a到b
plt.ylim((0, 130000)) #y轴的刻度范围被设为a'到b'
plt.show()
import pandas as pd
#导入数据集
income = pd.read_csv(r'Salary_Data.csv')
#样本量
n = income.shape[0]
#计算自变量、因变量、自变量平方、自变量与因变量乘积的和
sum_x = income.YearsExperience.sum() #自变量x的和
sum_y = income.Salary.sum() #因变量y的和
sum_x2 = income.YearsExperience.pow(2).sum() #自变量平方的和
xy = income.YearsExperience * income.Salary #自变量与因变量乘积
sum_xy = xy.sum() #自变量与因变量乘积的和
#计算回归系数a,b
b = (sum_xy - (sum_x*sum_y)/n) / (sum_x2 - sum_x**2/n)
a = income.Salary.mean() - b*income.YearsExperience.mean()
print('一元拟合函数的斜率b:',b)
print('一元拟合函数的截距a:',a)
结果:
一元拟合函数的斜率b: 9449.962321455081
一元拟合函数的截距a: 25792.200198668666
计算回归模型的第三方模块statsmodels中的ols函数
如上所示,利用Python的计算功能,最终得到模型的回归参数值。你可能会觉得麻烦,为了计算回归模型的参数还得人工写代码,是否有现成的第三方模块可以直接调用呢?答案是肯定的,这个模块就是statsmodels,它是专门用于统计建模的第三方模块,如需实现线性回归模型的参数求解,可以调用子模块中的ols函数。有关该函数的语法及参数含义可见下方:
ols(formula, data, subset=None, drop_cols=None)
- formula:以字符串的形式指定线性回归模型的公式,如’y~x’就表示简单线性回归模型。
- data:指定建模的数据集。
- subset:通过bool类型的数组对象,获取data的子集用于建模。
- drop_cols:指定需要从data中删除的变
这是一个语法非常简单的函数,而且参数也通俗易懂,但该函数的功能却很强大,不仅可以计算模型的参数,还可以对模型的参数和模型本身做显著性检验、计算模型的决定系数等。接下来,利用该函数计算模型的参数值,进而验证手工方式计算的参数是否正确:
import pandas as pd
import statsmodels.api as sm
#导入数据集
income = pd.read_csv(r'Salary_Data.csv')
#利用收入数据集,构建回归模型
fit = sm.formula.ols('Salary ~ YearsExperience', data=income).fit()
#返回模型的参数值
print(fit.params)
结果:
Intercept 25792.200199
YearsExperience 9449.962321
dtype: float64
如上结果所示,Intercept表示截距项对应的参数值,
YearsExperience表示自变量工作年限对应的参数值。对比发现,函数计
算出来的参数值与手工计算的结果完全一致,所以,关于收入的简单线
性回归模型可以表示成:
Salary = 25792.20 + 9449.96YearsExperience
多元线性回归模型
一元线性回归模型反映的是单个自变量对因变量的影响,然而实际情况中,影响因变量的自变量往往不止一个,从而需要将一元线性回归模型扩展到多元线性回归模型。
如果构建多元线性回归模型的数据集包含n个观测、p+1个变量(其中p个自变量和1个因变量),则这些数据可以写成下方的矩阵形式:
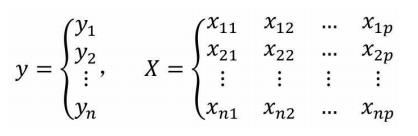
其中,xij代表第个i行的第j个变量值。如果按照一元线性回归模型的逻辑,那么多元线性回归模型应该就是因变量y与自变量X的线性组合,即可以将多元线性回归模型表示成:
y=β0+β1x1+β2x2+…+βpxn+ε
根据线性代数的知识,可以将上式表示成y=Xβ+ε。
其中,
β为p×1的一维向量,代表了多元线性回归模型的偏回归系数;
ε为n×1的一维向量,代表了模型拟合后每一个样本的误差项。
回归模型的参数求解
在多元线性回归模型所涉及的数据中,因变量y是一维向量,而自变量X为二维矩阵,所以对于参数的求解不像一元线性回归模型那样简单,但求解的思路是完全一致的。为了使读者掌握多元线性回归模型参数的求解过程,这里把详细的推导步骤罗列到下方:
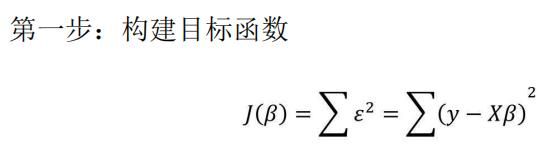
根据线性代数的知识,可以将向量的平方和公式转换为向量的内积,接下来需要对该式进行平方项的展现。


经过如上四步的推导,最终可以得到偏回归系数β与自变量X、因变量y的数学关系。这个求解过程也被成为“最小二乘法”。基于已知的偏回归系数β就可以构造多元线性回归模型。前文也提到,构建模型的最终目的是为了预测,即根据其他已知的自变量X的值预测未知的因变量y的值。
回归模型的预测
如果已经得知某个多元线性回归模型y=β0+β1x1+β2x2+…+βpxn,当有其他新的自变量值时,就可以将这些值带入如上的公式中,最终得到未知的y值。在Python中,实现线性回归模型的预测可以使用predict“方法”,关于该“方法”的参数含义如下:
predict(exog=None, transform=True)
- exog:指定用于预测的其他自变量的值。
- transform:bool类型参数,预测时是否将原始数据按照模型表达式进行转换,默认为True。
接下来将基于statsmodels模块对多元线性回归模型的参数进行求解,进而依据其他新的自变量值实现模型的预测功能。这里不妨以某产品的利润数据集为例,该数据集包含5个变量,分别是产品的研发成本、管理成本、市场营销成本、销售市场和销售利润,数据集的部分截图如下表所示。
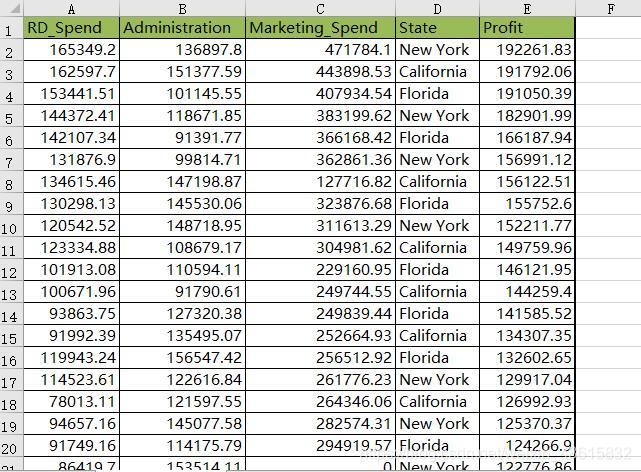
上图表中数据集中的Profit变量为因变量,其他变量将作为模型的自变量。需要注意的是,数据集中的State变量为字符型的离散变量,是无法直接带入模型进行计算的,所以建模时需要对该变量进行特殊处理。
(sklearn是python的重要机器学习库,其中封装了大量的机器学习算法,如:分类、回归、降维以及聚类;还包含了监督学习、非监督学习、数据变换三大模块。sklearn拥有完善的文档,使得它具有了上手容易的优势;并它内置了大量的数据集,节省了获取和整理数据集的时间。因而,使其成为了广泛应用的重要的机器学习库。ML神器:sklearn的快速使用)
有关产品利润的建模和预测过程如下代码所示:
from sklearn import model_selection
import pandas as pd
import statsmodels.api as sm
#导入数据
Profit = pd.read_excel(r'Predict to Profit.xlsx')
#将数据集拆分为训练集和测试集
train, test = model_selection.train_test_split(Profit, test_size=0.2, random_state=1234)
#根据train数据集建模
model = sm.formula.ols('Profit ~ RD_Spend + Administration + Marketing_Spend + C(State)', data=train).fit()
print('模型的偏回归系数分别为:\n', model.params)
#删除test数据集中的Profit变量,用剩下的自变量进行预测
test_X = test.drop(labels='Profit', axis=1)
pred = model.predict(exog=test_X)
print('对比预测值和实际值的差异:\n', pd.DataFrame({'Prediction': pred, 'Real':test.Profit}))
结果:
模型的偏回归系数分别为:
Intercept 58581.516503
C(State)[T.Florida] 927.394424
C(State)[T.New York] -513.468310
RD_Spend 0.803487
Administration -0.057792
Marketing_Spend 0.013779
dtype: float64
对比预测值和实际值的差异:
Prediction Real
8 150621.345801 152211.77
48 55513.218079 35673.41
14 150369.022458 132602.65
42 74057.015562 71498.49
29 103413.378282 101004.64
44 67844.850378 65200.33
4 173454.059691 166187.94
31 99580.888894 97483.56
13 128147.138396 134307.35
18 130693.433835 124266.90
Profit = 58581.52 + 0.80RD_Spend - 0.06Administation + 0.01Marketing_Spend + 927.39Florda - 513.47New York
如上结果所示,得到多元线性回归模型的回归系数及测试集上的预测值,为了比较,将预测值和测试集中的真实Profit值罗列在一起。针对如上代码需要说明三点:
- 为了建模和预测,将数据集拆分为两部分,分别是训练集(占80%)和测试集(占20%),训练集用于建模,测试集用于模型的预测。
- 由于数据集中的State变量为非数值的离散变量,故建模时必须将其设置为哑变量的效果,实现方式很简单,将该变量套在C()中,表示将其当作分类(Category)变量处理。
- 对于predict“方法”来说,输入的自变量X与建模时的自变量X必须保持结构一致,即变量名和变量类型必须都相同,这就是为什么代码中需要将test数据集的Profit变量删除的原因。
对于输出的回归系数结果,读者可能会感到疑惑,为什么字符型变量State对应两个回归系数,而且标注了Florida和New York。那是因为字符型变量State含有三种不同的值,分别是California、Florida和NewYork,在建模时将该变量当作哑变量处理,所以三种不同的值就会衍生出两个变量,分别是State[Florida]和State[New York],而另一个变量State[California]就成了对照组。
正如建模中的代码所示,将State变量套在C()中,就表示State变量需要进行哑变量处理。但是这样做会存在一个缺陷,那就是无法指定变量中的某个值作为对照组,正如模型结果中默认将State变量的California值作为对照组(因为该值在三个值中的字母顺序是第一个)。如需解决这个缺陷,就要通过pandas模块中的get_dummies函数生成哑变量,然后将所需的对照组对应的哑变量删除即可。为了使读者明白该解决方案,这里不妨重新建模,并以State变量中的New York值作为对照组,代码如下:
from sklearn import model_selection
import pandas as pd
import statsmodels.api as sm
#横向最多显示多少个字符, 一般80不适合横向的屏幕,平时多用200
pd.set_option('display.width', 200)
#显示所有列
pd.set_option('display.max_columns',None)
#显示所有行
pd.set_option('display.max_rows', None)
#导入数据
Profit = pd.read_excel(r'Predict to Profit.xlsx')
#生成由State变量衍生的哑变量
dummies = pd.get_dummies(Profit.State)
print(dummies)
#将哑变量与原始数据集水平合并
Profit_New = pd.concat([Profit, dummies], axis=1)
print('Profit_New:\n',Profit_New)
#删除State变量和New York变量(因为State变量已被分解为哑变量,New York变量需要作为参照组)
Profit_New.drop(labels=['State', 'New York'], axis=1, inplace=True)
#将数据集拆分为训练集和测试集
train, test = model_selection.train_test_split(Profit_New, test_size=0.2, random_state=1234)
#根据train数据集建模
model = sm.formula.ols('Profit ~ RD_Spend + Administration + Marketing_Spend + Florida + California', data=train).fit()
print('模型的偏回归系数分别为:\n', model.params)
#删除test数据集中的Profit变量,用剩下的自变量进行预测
test_X = test.drop(labels='Profit', axis=1)
pred = model.predict(exog=test_X)
print('对比预测值和实际值的差异:\n', pd.DataFrame({'Prediction': pred, 'Real':test.Profit}))
结果:
California Florida New York
0 0 0 1
1 1 0 0
2 0 1 0
3 0 0 1
4 0 1 0
5 0 0 1
6 1 0 0
7 0 1 0
8 0 0 1
9 1 0 0
10 0 1 0
11 1 0 0
12 0 1 0
13 1 0 0
14 0 1 0
15 0 0 1
16 1 0 0
17 0 0 1
18 0 1 0
19 0 0 1
20 1 0 0
21 0 0 1
22 0 1 0
23 0 1 0
24 0 0 1
25 1 0 0
26 0 1 0
27 0 0 1
28 0 1 0
29 0 0 1
30 0 1 0
31 0 0 1
32 1 0 0
33 0 1 0
34 1 0 0
35 0 0 1
36 0 1 0
37 1 0 0
38 0 0 1
39 1 0 0
40 1 0 0
41 0 1 0
42 1 0 0
43 0 0 1
44 1 0 0
45 0 0 1
46 0 1 0
47 1 0 0
48 0 0 1
Profit_New:
RD_Spend Administration Marketing_Spend State Profit California Florida New York
0 165349.20 136897.80 471784.10 New York 192261.83 0 0 1
1 162597.70 151377.59 443898.53 California 191792.06 1 0 0
2 153441.51 101145.55 407934.54 Florida 191050.39 0 1 0
3 144372.41 118671.85 383199.62 New York 182901.99 0 0 1
4 142107.34 91391.77 366168.42 Florida 166187.94 0 1 0
5 131876.90 99814.71 362861.36 New York 156991.12 0 0 1
6 134615.46 147198.87 127716.82 California 156122.51 1 0 0
7 130298.13 145530.06 323876.68 Florida 155752.60 0 1 0
8 120542.52 148718.95 311613.29 New York 152211.77 0 0 1
9 123334.88 108679.17 304981.62 California 149759.96 1 0 0
10 101913.08 110594.11 229160.95 Florida 146121.95 0 1 0
11 100671.96 91790.61 249744.55 California 144259.40 1 0 0
12 93863.75 127320.38 249839.44 Florida 141585.52 0 1 0
13 91992.39 135495.07 252664.93 California 134307.35 1 0 0
14 119943.24 156547.42 256512.92 Florida 132602.65 0 1 0
15 114523.61 122616.84 261776.23 New York 129917.04 0 0 1
16 78013.11 121597.55 264346.06 California 126992.93 1 0 0
17 94657.16 145077.58 282574.31 New York 125370.37 0 0 1
18 91749.16 114175.79 294919.57 Florida 124266.90 0 1 0
19 86419.70 153514.11 0.00 New York 122776.86 0 0 1
20 76253.86 113867.30 298664.47 California 118474.03 1 0 0
21 78389.47 153773.43 299737.29 New York 111313.02 0 0 1
22 73994.56 122782.75 303319.26 Florida 110352.25 0 1 0
23 67532.53 105751.03 304768.73 Florida 108733.99 0 1 0
24 77044.01 99281.34 140574.81 New York 108552.04 0 0 1
25 64664.71 139553.16 137962.62 California 107404.34 1 0 0
26 75328.87 144135.98 134050.07 Florida 105733.54 0 1 0
27 72107.60 127864.55 353183.81 New York 105008.31 0 0 1
28 66051.52 182645.56 118148.20 Florida 103282.38 0 1 0
29 65605.48 153032.06 107138.38 New York 101004.64 0 0 1
30 61994.48 115641.28 91131.24 Florida 99937.59 0 1 0
31 61136.38 152701.92 88218.23 New York 97483.56 0 0 1
32 63408.86 129219.61 46085.25 California 97427.84 1 0 0
33 55493.95 103057.49 214634.81 Florida 96778.92 0 1 0
34 46426.07 157693.92 210797.67 California 96712.80 1 0 0
35 46014.02 85047.44 205517.64 New York 96479.51 0 0 1
36 28663.76 127056.21 201126.82 Florida 90708.19 0 1 0
37 44069.95 51283.14 197029.42 California 89949.14 1 0 0
38 20229.59 65947.93 185265.10 New York 81229.06 0 0 1
39 38558.51 82982.09 174999.30 California 81005.76 1 0 0
40 28754.33 118546.05 172795.67 California 78239.91 1 0 0
41 27892.92 84710.77 164470.71 Florida 77798.83 0 1 0
42 23640.93 96189.63 148001.11 California 71498.49 1 0 0
43 15505.73 127382.30 35534.17 New York 69758.98 0 0 1
44 22177.74 154806.14 28334.72 California 65200.33 1 0 0
45 1000.23 124153.04 1903.93 New York 64926.08 0 0 1
46 1315.46 115816.21 297114.46 Florida 49490.75 0 1 0
47 0.00 135426.92 0.00 California 42559.73 1 0 0
48 542.05 51743.15 0.00 New York 35673.41 0 0 1
模型的偏回归系数分别为:
Intercept 58068.048193
RD_Spend 0.803487
Administration -0.057792
Marketing_Spend 0.013779
Florida 1440.862734
California 513.468310
dtype: float64
对比预测值和实际值的差异:
Prediction Real
8 150621.345802 152211.77
48 55513.218079 35673.41
14 150369.022458 132602.65
42 74057.015562 71498.49
29 103413.378282 101004.64
44 67844.850378 65200.33
4 173454.059692 166187.94
31 99580.888895 97483.56
13 128147.138397 134307.35
18 130693.433835 124266.90
如上结果所示,从离散变量State中衍生出来的哑变量在回归系数的结果里只保留了Florida和California,而New York变量则作为了参照组。以该模型结果为例,得到的模型公式可以表达为:
Profit = 58068.05 + 0.80RD_Spend-0.06Administation + 0.01Marketing_Spend + 1440.86Florida + 513.47California
虽然模型的回归系数求解出来了,但从统计学的角度该如何解释模型中的每个回归系数呢?
下面分别以研发成本RD_Spend变量和哑变量Florida为例,解释这两个变量对模型的作用:在其他变量不变的情况下,研发成本每增加1美元,利润会增加0.80美元;在其他变量不变的情况下,以New York为基准线,如果在Florida销售产品,利润会增加1440.86美元。
关于产品利润的多元线性回归模型已经构建完成,但是该模型的好与坏并没有相应的结论,还需要进行模型的显著性检验和回归系数的显著性检验。
总结
在实际应用中,如果因变量为数值型变量,可以考虑使用线性回归模型。但是前提得满足几点假设,如Python数据分析与挖掘——回归模型的诊断:因变量服从正态分布、自变量间不存在多重共线性、自变量与因变量之间存在线性关系、用于建模的数据集不存在异常点、残差项满足方差异性和独立性。