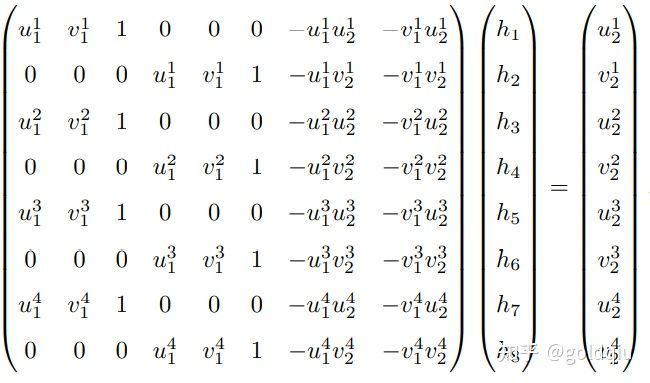视觉SLAM十四讲学习笔记-第七讲-视觉里程计-单应矩阵和实践

 专栏汇总

视觉SLAM十四讲学习笔记-第一讲_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第二讲-初识SLAM_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第二讲-开发环境搭建_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第三讲-旋转矩阵和Eigen库_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第三讲-旋转向量、欧拉角、四元数_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第三讲-相似、仿射、射影变换和eigen程序、可视化演示_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记---前三讲学习笔记总结之SLAM的作用、变换和位姿表示_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第四讲-李代数求导与扰动模型_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第四讲-Sophus实践、相似变换群与李代数_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第五讲-相机模型_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第五讲-图像和实践_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第四讲---第五讲学习笔记总结---李群和李代数、相机_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第六讲-非线性优化的非线性最小二乘问题_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第六讲-非线性优化的实践-高斯牛顿法和曲线拟合_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第六讲学习笔记总结（1）---非线性优化原理_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第六讲学习笔记总结（2）---非线性优化应用_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第七讲-视觉里程计-特征点发和特征提取和匹配实践_goldqiu的博客-CSDN博客

视觉SLAM十四讲学习笔记-第七讲-视觉里程计-对极几何和对极约束、本质矩阵、基础矩阵

7.3.3单应矩阵

单应矩阵（Homography）H ，描述了两个平面之间的映射关系。若场景中的特征点都落在同一平面上（比如墙，地面等），则可以通过单应性来进行运动估计。这种情况在无人机携带的俯视相机，或扫地机携带的顶视相机中比较常见。单应矩阵通常描述处于共同平面上的一些点，在两张图像之间的变换关系。考虑在图像I1和I2有一对匹配好的特征点p1和p2。这些特征点落在某平面上。设这个平面满足方程：

然后代入

得：

把直接描述图像坐标 p1 和 p2 之间的变换的中间这部分记为 H，于是 p2 = Hp1。它的定义与旋转、平移以及平面的参数有关。单应矩阵H是一个 3 × 3 的矩阵，求解时的思路可以先根据匹配点计算H，然后将它分解以计算旋转和平移。把上式展开，得：

注意这里的等号是在非零因子下成立的。在实际处理中，通常乘以一个非零因子使得 h9 = 1（在它取非零值时）。然后根据第三行，去掉这个非零因子，于是有：

这样一组匹配点对就可以构造出两项约束（事实上有三个等式，但是因为线性相关，只取前两个），于是自由度为 8 的单应矩阵可以通过 4 对匹配特征点算出（注意：这些特征点不能有三点共线的情况），即求解以下的线性方程组（当 h9 = 0 时，右侧为零）：

这种做法把H矩阵看成了向量，通过解该向量的线性方程来恢复H，又称直接线性变换法（Direct Linear Transform）。求出单应矩阵以后需要对其进行分解，才可以得到相应的旋转矩阵 R 和平移向量 t。分解的方法包括数值法与解析法 。单应矩阵的分解会返回四组旋转矩阵与平移向量，并且同时可以计算出它们分别对应的场景点所在平面的法向量。如果已知成像的地图点的深度全为正值（即在相机前方），则又可以排除两组解。最后仅剩两组解，这时需要通过更多的先验信息进行判断。通常可以通过假设已知场景平面的法向量来解决，如场景平面 与相机平面平行，那么法向量n的理论值为1。

单应性在 SLAM 中具有重要意义。当特征点共面，或者相机发生纯旋转的时候，基础矩阵的自由度下降，这就出现了所谓的退化（degenerate）。现实中的数据总包含一些噪声， 这时候如果继续使用八点法求解基础矩阵，基础矩阵多余出来的自由度将会主要由噪 声决定。为了能够避免退化现象造成的影响，通常会同时估计基础矩阵 F 和单应矩阵 H，选择重投影误差比较小的那个作为最终的运动估计矩阵。

7.4 实践：对极约束求解相机运动

如何通过 Essential 矩阵求解相机运动？

使用匹配好的特征点来计算 E,F 和 H，进而分解 E 得 到 R, t。整个程序使用 OpenCV 提供的算法进行求解。

代码：slambook/ch7/pose_estimation_2d2d.cpp

pose_estimation_2d2d函数提供了从特征点求解相机运动的部分，在函数中输出了 E,F 和 H 的数值，然后验证对极约束是否成立，以及 t ∧R 和 E 在非零数乘下等价的事实。调用此程序的输出结果：

build/pose_estimation_2d2d 1.png 2.png
-- Max dist : 95.000000
-- Min dist : 4.000000
一共找到了 79 组匹配点
fundamental_matrix is
[4.844484382466111e-06, 0.0001222601840188731, -0.01786737827487386;
-0.0001174326832719333, 2.122888800459598e-05, -0.01775877156212593;
0.01799658210895528, 0.008143605989020664, 1]
essential_matrix is
[-0.0203618550523477, -0.4007110038118445, -0.03324074249824097;
0.3939270778216369, -0.03506401846698079, 0.5857110303721015;
-0.006788487241438284, -0.5815434272915686, -0.01438258684486258]
homography_matrix is
[0.9497129583105288, -0.143556453147626, 31.20121878625771;
0.04154536627445031, 0.9715568969832015, 5.306887618807696;
-2.81813676978796e-05, 4.353702039810921e-05, 1]
R is
[0.9985961798781875, -0.05169917220143662, 0.01152671359827873;
0.05139607508976055, 0.9983603445075083, 0.02520051547522442;
-0.01281065954813571, -0.02457271064688495, 0.9996159607036126]
t is
[-0.8220841067933337;
-0.03269742706405412;
0.5684264241053522]
​
t^R=
[0.02879601157010516, 0.5666909361828478, 0.04700950886436416;
-0.5570970160413605, 0.0495880104673049, -0.8283204827837456;
0.009600370724838804, 0.8224266019846683, 0.02034004937801349]
epipolar constraint = [0.002528128704106625]
epipolar constraint = [-0.001663727901710724]
epipolar constraint = [-0.0008009088410884102

可以看出，对极约束的满足精度约在 10−3 量级。OpenCV 使用三角化检测角点的深度是否为正，从而选出正确的解。 对极约束是从 x2 = Rx1 + t 得到的。这里的 R, t 组成的变换矩阵，是第一个图到第二个图的坐标变换矩阵： x2 = T21x1.

7.4.1 讨论

从演示程序中可以看到，输出的 E 和 F 相差了相机内参矩阵。从 E,F 和 H 都可以分解出运动，不过 H 需要假设特征点位于平面上。 由于 E 本身具有尺度等价性，它分解得到的 t, R 也有一个尺度等价性。而 R ∈ SO(3) 自身具有约束，所以认为 t 具有一个尺度。换言之，在分解过程中，对 t 乘以任意非零常数，分解都是成立的。因此通常把 t 进行归一化，让它的长度等于 1。

尺度不确定性

对 t 长度的归一化，直接导致了单目视觉的尺度不确定性（Scale Ambiguity）。例如，程序中输出的 t 第一维约 0.822。这个 0.822 究竟是指 0.822 米呢，还是 0.822 厘米 呢，是没法确定的。因为对 t 乘以任意比例常数后，对极约束依然是成立的。换言之， 在单目 SLAM 中，对轨迹和地图同时缩放任意倍数，得到的图像依然是一样的。 在单目视觉中，对两张图像的 t 归一化，相当于固定了尺度。虽然不知道它的实际长度为多少，但以这时的 t 为单位 1，计算相机运动和特征点的 3D 位置。这被称为单目 SLAM 的初始化。在初始化之后，就可以用 3D-2D 来计算相机运动了。初始化之后的轨迹和地图的单位，就是初始化时固定的尺度。因此，单目 SLAM 有一步不可避免的初始化。初始化的两张图像必须有一定程度的平移，而后的轨迹和地图都将以此步的平移为单位。 除了对 t 进行归一化之外，另一种方法是令初始化时所有的特征点平均深度为 1，也 可以固定一个尺度。相比于令 t 长度为 1 的做法，把特征点深度归一化可以控制场景的规模大小，使计算在数值上更稳定些。

初始化的纯旋转问题

从 E 分解到 R, t 的过程中，如果相机发生的是纯旋转，导致 t 为零，那么，得到的 E 也将为零，这将导致无从求解 R。不过，此时可以依靠 H 求取旋转，但仅有旋转时，无法用三角测量估计特征点的空间位置，于是，另一个结论是，单目初始化不能只有纯旋转，必须要有一定程度的平移。如果没有平移，单目将无法初始化。在实践当中，如果初始化时平移太小，会使得位姿求解与三角化结果不稳定， 从而导致失败。相对的，如果把相机左右移动而不是原地旋转，就容易让单目 SLAM 初始化。

多于八对点的情况

当给定的点数多于八对时，可以计算一个最小二乘解。对于线性化后的对极约束，我们把左侧的系数矩阵记为 A： Ae = 0

对于八点法，A 的大小为 8 × 9。如果给定的匹配点多于 8，该方程构成一个超定方程，即不一定存在 e 使得上式成立。因此，可以通过最小化一个二次型来求：

于是就求出了在最小二乘意义下的 E 矩阵。不过，当可能存在误匹配的情况时，会更倾向于使用随机采样一致性（Random Sample Concensus, RANSAC）来求，而不是最小二乘。RANSAC 是一种通用的做法，适用于很多带错误数据的情况，可以处理带有错误匹配的数据。