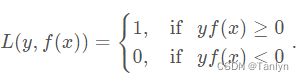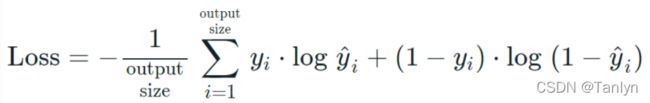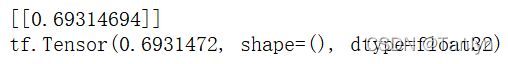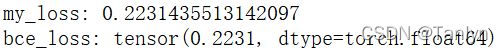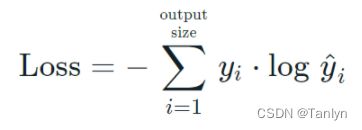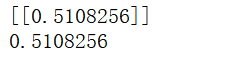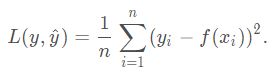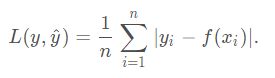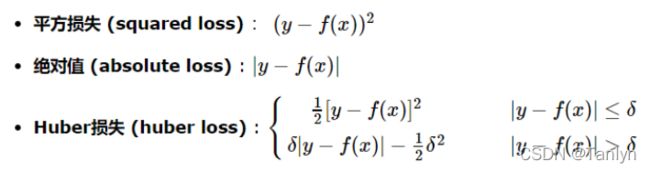《python深度学习》笔记（十一）：损失函数

1.定义

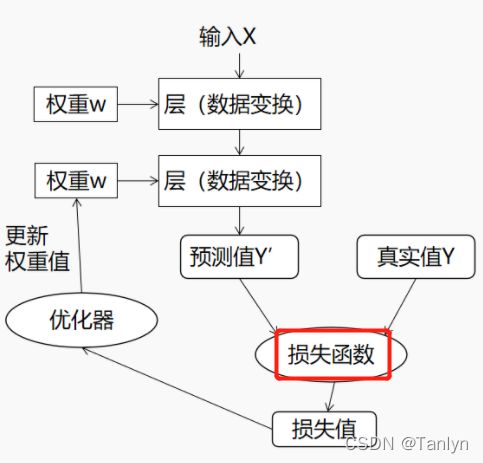
 损失函数的一般表示为 L(y,f(x))，用以衡量真实值 y和预测值 f(x)之间不一致的程度，一般越小越好。为了便于不同损失函数的比较，常将其表示为单变量的函数，在回归问题中这个变量为 [y-f(x)] ：残差表示，在分类问题中则为 yf(x) ： 趋势一致。

具有多个输出的神经网络可能具有多个损失函数，每个输出对应一个损失函数。但是梯度下降过程必须基于单个标量的损失值。因此，对于多个损失函数的网络，需要将其所有损失值取平均，变成一个标量值。

2.分类 

2.1分类问题

对于二分类问题，标签y ∈ { + 1 , − 1 }。损失函数常表示为关于y f ( x )的单调递减形式。如下图所示：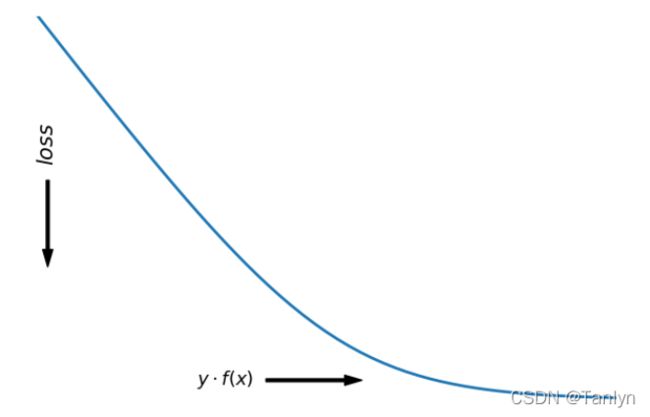

 yf(x)被称为是间隔margin，显然y f ( x ) > 0 说明分类器分类正确，y f ( x ) < 0 ，说明分类器分类错误。其中f ( x ) 就是分类器的超平面。这让我们联想到了例如感知机，支持向量机等的分类问题，最小化损失函数就是最大化margin的一个过程。

2.1.1 0-1损失（0-1 loss）

函数公式如下：

                             

 0-1损失对任何分类错误的点的对待是相同的，即使是偏远点也一样。0-1损失是离散的、非凸函数，因此优化困难。因而常使用其他的代理损失函数进行优化。

2.1.2 交叉熵损失（cross entropy loss）

交叉熵损失是深度学习的分类问题中常用的损失函数。交叉熵也是是信息论中的一个重要概念，主要用于度量两个概率分布间的差异性。这里不讲交叉熵理论的详细知识，只展现具体的代码实现。

使用交叉熵的背景：

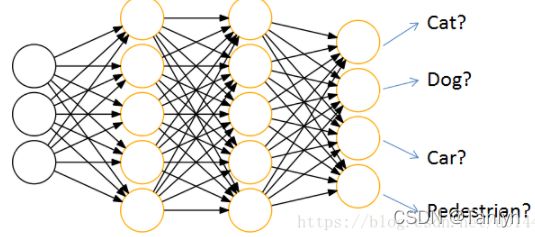
通过神经网络解决分类问题时，一般会设置k个输出点，k代表类别的个数，如下图：

每个输出结点，都会输出该结点对应类别的得分，如[cat，dog，car，pedestrian] 为[44，10，22，5]。但是输出结点输出的是得分，而不是概率分布，那么就没有办法用交叉熵来衡量预测结果和真确结果了，那怎么办呢，解决方法是在输出结果后接一层 softmax，softmax的作用就是把输出得分换算为概率分布。

 

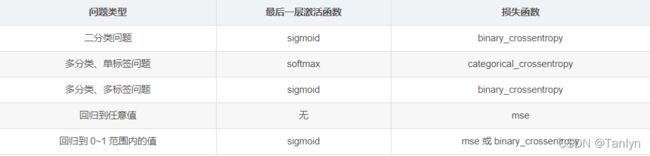
二分类问题：二元交叉熵（binary_cross_entropy）

                                        

使用tensorflow实现：

# 当batch_size为1，标签总数为1，即输出shape为(1,1,1)时
import tensorflow as tf
y_true = [[[0.]]]
y_pred = [[[0.5]]]
# 用自带函数实现
loss = tf.keras.losses.binary_crossentropy(y_true, y_pred)
loss.numpy()
print(loss.numpy())
print
# 自己编码用公式实现
loss_1 = -(1/1)*( 0*tf.math.log(0.5) +(1-0)*tf.math.log(1-0.5))
print(loss_1)

 

使用pytorch实现：

import numpy as np
import torch
import torch.nn.functional as F
y_true = np.array([0., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
y_pred = np.array([0.2, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8])
# 自己编码用公式计算
my_loss = - y_true * np.log(y_pred) - (1 - y_true) * np.log(1 - y_pred)
mean_my_loss = np.mean(my_loss)
print('my_loss:', mean_my_loss)
# 使用pytorch自带的函数计算
torch_pred = torch.tensor(y_pred)
torch_true = torch.tensor(y_true)
bce_loss = F.binary_cross_entropy(torch_pred, torch_true)
print('bce_loss:', bce_loss)

 

 多分类问题：分类交叉熵（categorical_cross_entropy）

                        

使用tensorflow实现：

import tensorflow as tf
y_true = [[[0.,1.]]]
y_pred = [[[0.4,0.6]]]# 假设已经经过了softmax，所以和必须为1
# 使用自带函数计算
loss = tf.keras.losses.categorical_crossentropy(y_true, y_pred)

print(loss.numpy())
# 使用公式编码计算
loss = -( 0*tf.math.log(0.4) + 1*tf.math.log(0.6) )
print(loss.numpy())

 

 

2.2 回归问题

回归问题的学习等价于函数拟合：选择一条函数曲线使其很好的拟合已知数据并很好地预测未知数据。所以回归问题中的y和f(x)均∈ R 且用残差y − f ( x )来度量回归问题的预测值和真实值的不一致程度。

2.2.1 均方误差损失（MSE，L2 loss）

均方误差损失又叫做L2损失，数学表达式如下：

                                             

 这是最常见的损失函数，是凸函数，可以使用梯度下降法进行优化。但对于远离真实值的点相对来说比较敏感，损失函数的代价值很大，这造成了均方误差损失函数的鲁棒性变差。

2.2.2 绝对值损失（MAE，L1 Loss）

绝对值损失函数又叫做L 1 L1L1损失函数，数学表达式如下：

                                            

 绝对值损失函数对偏远点的处理相对均方误差来说很好，但是在y = f ( x ) y=f(x)y=f(x)处是不可导函数，并且M A E MAEMAE更新的梯度始终相同，在接近最优值处仍可能维持着较大的梯度而错过最优值。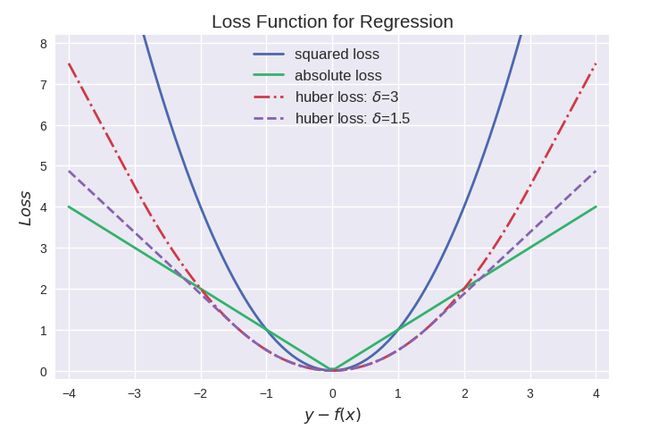

3.总结：

1.平方损失最常用，其缺点是对于异常点会施以较大的惩罚，因而不够robust。
2.绝对损失具有抵抗异常点干扰的特性，但是在y-f(x)处不连续可导，难以优化。
3.Huber损失是对二者的综合，当 |y-f(x)|小于一个事先指定的值 δ时，变为平方损失；大于δ时，则变成类似于绝对值损失，因此也是比较robust的损失函数。
4.如果异常点代表很重要的异常情况，且需要被检测出来，用MSE。回归问题常用MSE损失函数。如果只是把异常数据当做受损数据，用MAE。