利用跨模态 Transformer 进行多模态信息融合
目录
- 1. 简介
- 2. 创新点
- 3. 模型描述
-
- 3.1 Low Rank Fusion
- 3.2 Multimodal Transformer
-
- 具体模块介绍
-
- Temporal Convolutions
- Positional Embedding (PE)
- Crossmodal Attention (core)
- Crossmodal Transformers
- Self-Attention Transformers and Prediction
- 4. Experiment
1. 简介
前面文章提到基于张量低秩分解进行多模态的融合,今天介绍的文章则结合多模态 Transformer (MulT) [1] 和 低秩矩阵分解 (Low Rank Matrix Factorization, LMF)[2] 来处理多模态融合的问题,并且相对减少了跨模态 Transformer 的个数,没有引起过度的参数化。
本文内容包括了两篇文章的内容:
- Low Rank Fusion based Transformers for Multimodal Sequences ( LMF-MulT )
- Multimodal transformer for unaligned multimodal language sequences ( MulT )
2. 创新点
-
MulT方法 [1] 中有3个
unimodal transformer和 6 个bimodal transformer,但是没有 trimodel 。本文方法比 mulT 使用更少的 transformer 来得到多模态表示。 -
提出两种方法
- LMF-MulT:通过3个模态的注意力加强融合表示。
- Fusion-Based-CM-Attn:通过融合信号并行加强单个模态表示。
-
利用低秩矩阵分解的方法 (LMF) 通过近似张量融合来捕获所有单个模态、双模态以及三模态之间的交互。
-
文章可以处理对齐和非对齐的序列。可以对
非对齐序列进行建模的能力是有利的,因为文章依赖的是基于学习的方法,而不是使用强制信号同步的方法(需要额外的时间信息)来模仿人类多模态语言表达的协调性。
3. 模型描述
3.1 Low Rank Fusion
- LMF(low-rank matrix factorization)[2]:是一种张量融合方法,通过使用低秩分解因子来进行张量融合,避免了直接张量相成进行融合导致的高维问题,更多关于LMF的介绍可以看下这篇文章。
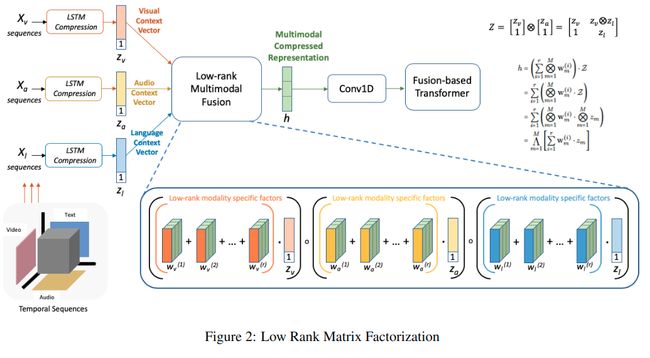
输入张量 Z ∈ R d 1 × d 2 × . . . × d m \mathcal{Z} \in \mathbb{R}^{d_1 \times d_2 \times...\times d_m} Z∈Rd1×d2×...×dm 通过一个线性层 g ( ⋅ ) g(\cdot) g(⋅) 产生一个向量表示:
h = g ( Z ; W , b ) = W ⋅ Z + b ; h , b ∈ R d y h = g(\mathcal{Z};\mathcal{W},b) = \mathcal{W} ⋅ \mathcal{Z} + b;~h, b \in \mathbb{R}^{d_y} h=g(Z;W,b)=W⋅Z+b; h,b∈Rdy
其中 W \mathcal{W} W 是权重, b b b 是偏移量。
基于 W \mathcal{W} W 的分解,再根据 Z = ⨂ m = 1 M z m \mathcal{Z}=\bigotimes_{m=1}^{M} z_{m} Z=⨂m=1Mzm ,可以把计算 h h h 的式子推算如下:
h = ( ∑ i = 1 r ⨂ m = 1 M w m ( i ) ) ⋅ Z = ∑ i = 1 r ( ⨂ m = 1 M w m ( i ) ⋅ Z ) = ∑ i = 1 r ( ⨂ m = 1 M w m ( i ) ⋅ ⨂ m = 1 M z m ) = ⋀ m = 1 M [ ∑ i = 1 r w m ( i ) ⋅ z m ] \begin{aligned} h &=\left(\sum_{i=1}^{r} \bigotimes_{m=1}^{M} \mathbf{w}_{m}^{(i)}\right) \cdot \mathcal{Z} =\sum_{i=1}^{r}\left(\bigotimes_{m=1}^{M} \mathbf{w}_{m}^{(i)} \cdot \mathcal{Z}\right) \\ &=\sum_{i=1}^{r}\left(\bigotimes_{m=1}^{M} \mathbf{w}_{m}^{(i)} \cdot \bigotimes_{m=1}^{M} z_{m}\right) \\ &=\bigwedge_{m=1}^{M}\left[\sum_{i=1}^{r} \mathbf{w}_{m}^{(i)} \cdot z_{m}\right] \end{aligned} h=(i=1∑rm=1⨂Mwm(i))⋅Z=i=1∑r(m=1⨂Mwm(i)⋅Z)=i=1∑r(m=1⨂Mwm(i)⋅m=1⨂Mzm)=m=1⋀M[i=1∑rwm(i)⋅zm]
如果通过计算 Z \mathcal{Z} Z再得到 h h h, m m m个模态 Z \mathcal{Z} Z的维度就是 d 1 × d 2 × . . . × d m d_1 \times d_2 \times...\times d_m d1×d2×...×dm,这种低秩分解代替原来的向量相成的方法,可以直接得到 h h h,不用计算高维的 Z \mathcal{Z} Z,使得可以轻松扩展到模态数较多的情况。
3.2 Multimodal Transformer
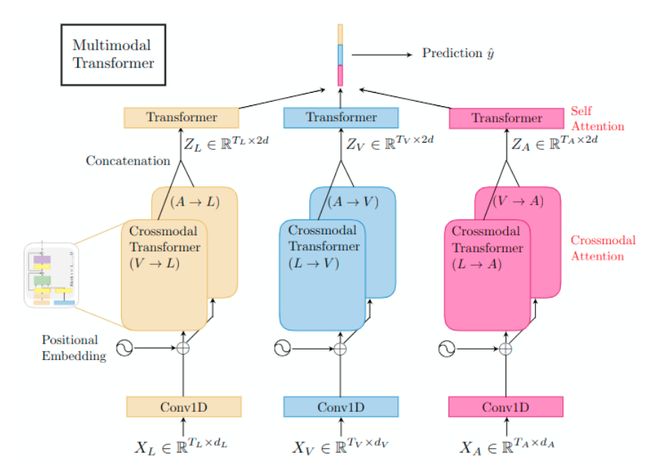
在基于 Transformers 的序列编码的基础上,利用 Tsai [1] 的 multiple cross-modal attention blocks 模块,然后用 self-attention 来编码多模态序列做分类。
- 早期工作关注一个模态到另外一个模态的潜在适应。文本关注利用single-head 和 cross-modal attention 实现潜在多模态融合表示与单个模态之间的适应。
- LMF 后加时间卷积。
文章这里用了两种框架:
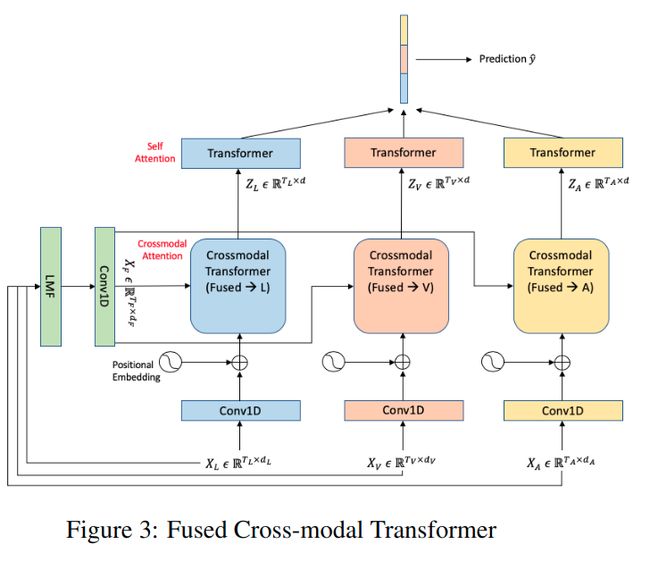
第一种框架是LMF得到的融合表示和每个模态表示之间建立一个跨模 transformer,然后利用融合表示加强单个模态的表示,最后将每个模态的表示连接在一起获得一个统一的表示去做后续的任务。
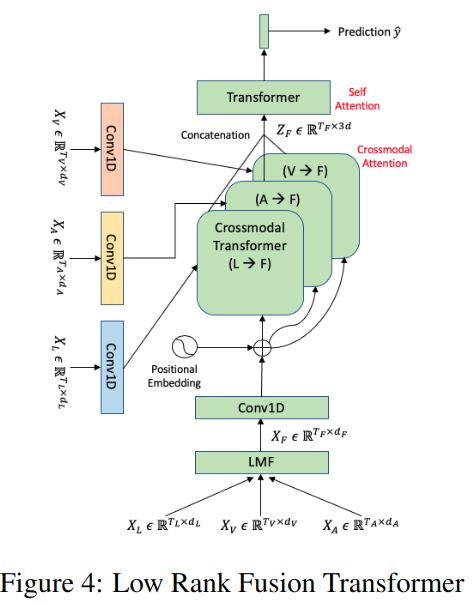
第二种框架是通过LMF得到的多模态融合表示,然后添加时间卷积信息和位置信息,然后基于每个模态的表示加强多模态融合表示,再对统一的表示进行self-attension,再进行后续任务。
具体模块介绍
- 论文中的各个模块没有具体的介绍,基础模块基于另外一篇ACL的论文:
Multimodal Transformer for Unaligned Multimodal Language Sequences (MulT)[1] ,这篇论文的框架图如下所示:
MulT 包括以下几个模块:
Temporal Convolutions
- 卷积得到的序列被期望包含序列的局部信息。
- k k k:对应模态卷积核的大小。
- 将不同模态的特征维度映射到 d d d,使得跨模注意力模块点积 (dot-products) 可用。
Positional Embedding (PE)
为了保证序列携带时间信息,为包含时间信息的表示 X ^ { L , V , A } \hat{X}_{\{L, V, A\}} X^{L,V,A} 增加位置嵌入 (position embedding, PE):
Z { L , V , A } [ 0 ] = X ^ { L , V , A } + PE ( T { L , V , A } , d ) Z_{\{L, V, A\}}^{[0]}=\hat{X}_{\{L, V, A\}}+\operatorname{PE}\left(T_{\{L, V, A\}}, d\right) Z{L,V,A}[0]=X^{L,V,A}+PE(T{L,V,A},d)
其中 PE ( T { L , V , A } , d ) ∈ R T { L , V , A } × d \operatorname{PE}\left(T_{\{L, V, A\}}, d\right) \in \mathbb{R}^{T_{\{L, V, A\}} \times d} PE(T{L,V,A},d)∈RT{L,V,A}×d,计算每个位置索引的嵌入,计算方式如下:
PE [ i , 2 j ] = sin ( i 1000 0 2 j d ) PE [ i , 2 j + 1 ] = cos ( i 1000 0 2 j d ) \begin{aligned} \operatorname{PE}[i, 2 j] &=\sin \left(\frac{i}{10000^{\frac{2 j}{d}}}\right) \\ \operatorname{PE}[i, 2 j+1] &=\cos \left(\frac{i}{10000^{\frac{2 j}{d}}}\right) \end{aligned} PE[i,2j]PE[i,2j+1]=sin(10000d2ji)=cos(10000d2ji)
其中 i = 1 , ⋯ , T i = 1,\cdots,T i=1,⋯,T 且 j = 0 , ⌊ d 2 ⌋ j = 0,\left\lfloor\frac{d}{2}\right\rfloor j=0,⌊2d⌋
Z { L , V , A } [ 0 ] Z_{\{L, V, A\}}^{[0]} Z{L,V,A}[0]就是不同模态包含低层位置信息的特征。
Crossmodal Attention (core)
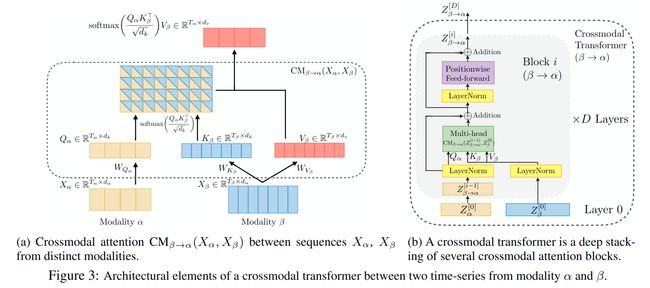
一种融合跨模信息的方式:提供一种潜在的跨模适应 ( latent adaptation across modalities ), 如下图中的模态 β \beta β 到模态 α \alpha α。
Crossmodal Transformers
基于跨模注意力模块,可以设计跨模transformer模块,使一个模态从另外一个模态接收信息。
以模态 vision ( V )到每模态 language ( L )为例:
每个跨模 transformer 都由 D 层 跨模注意力块组成。跨模态 transformer 对 1:D 层计算 feed-forwardly (前馈) 如下:
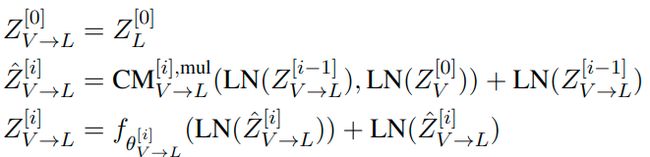
- f θ f_{\theta} fθ 是一个以 θ \theta θ 为参数的位置前馈子层
- C M V → L [ i ] , m u l \mathbf{CM}_{V \rightarrow L}^{[i], mul} CMV→L[i],mul 是第 i i i 层从模态 V V V 到模态 L L L multi-head 版的跨模注意力 ( crossmodal attention )
- L N \mathbf{LN} LN:layer normalization
在每对模态之间建立跨模交互,所以有6个跨模transformer。(MulT)
Self-Attention Transformers and Prediction
连接所有的跨模 transfomer 的输出,得到 Z { L , V , A } ∈ R T { L , V , A } × 2 d Z_{\{L, V, A\}} \in \mathbb{R}^{T}\{L, V, A\} \times 2 d Z{L,V,A}∈RT{L,V,A}×2d,例如 Z L = [ Z V → L [ D ] ; Z A → L [ D ] ] Z_{L}=\left[Z_{V \rightarrow L}^{[D]} ; Z_{A \rightarrow L}^{[D]}\right] ZL=[ZV→L[D];ZA→L[D]]
4. Experiment
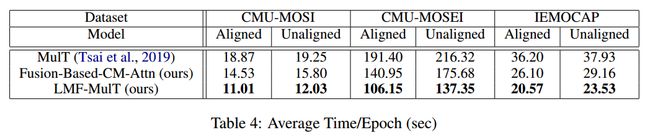
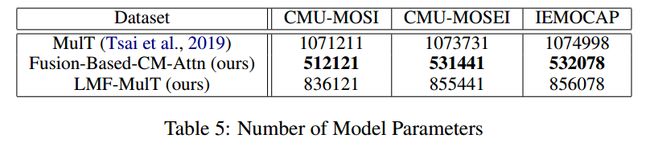
论文 Low Rank Fusion based Transformers for Multimodal Sequences 在三个多模态数据集上做了实验,
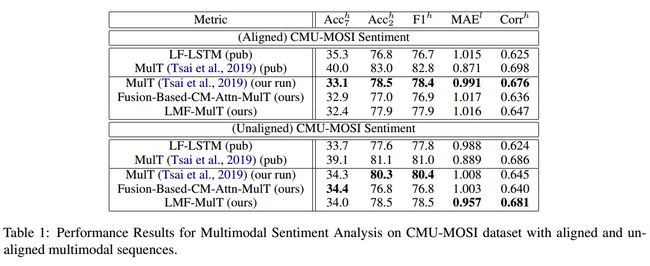
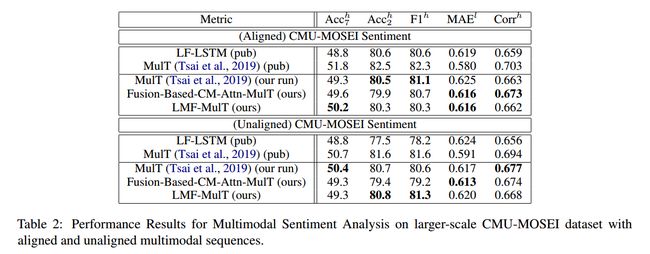
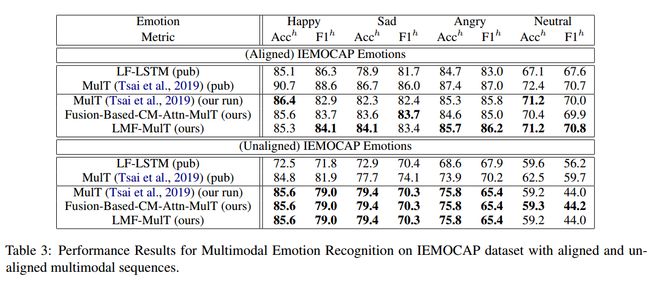
可以达到和他改进的 MulT 方法 comparable 的结果,但是相比 MulT,文章具有以下优点:
[1] Tsai, Yao-Hung Hubert, et al. "Multimodal transformer for unaligned multimodal language sequences." Proceedings of the conference. Association for Computational Linguistics. Meeting. Vol. 2019. NIH Public Access, 2019. [2] Liu, Zhun, Shen, Ying, et al. "Efficient Low-rank Multimodal Fusion With Modality-Specific Factors" Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics. Vol. 2018. NIH Public Access, 2018.