【解题报告】《LeetCode零基础指南》(第三讲) 循环

☘前言☘

今天是九日集训第二天，我会记录一下学习内容和题解，争当课代表0.0.
注意！！！！题解的解法一是今天要掌握的解法，解法2是学有余力再研究，涉及到后面知识点0.0
链接：《LeetCode零基础指南》(第二讲) 函数
另外：昨天讲过的知识点我今天不会再放有需要请查看：
【解题报告】《LeetCode零基础指南》(第二讲) 函数

作者简介：一个从工业设计改行学嵌入式的年轻人
✨联系方式：2201891280(QQ)
⏳全文大约阅读时间： 15min

---

---

主要知识点梳理

循环的使用

在C/C++语言中有两种结构：while和for，但是在很多情况下，两者没有太多本质差别，所以我们学习相对应用更方便的for语句。

1.语法规则

	for语句的表现形式是：

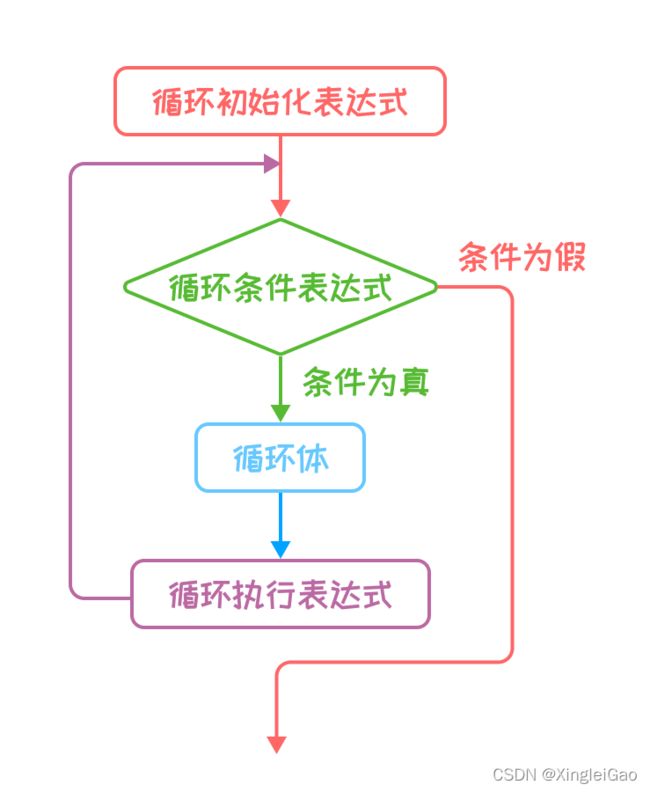
for(循环初始化表达式;循环条件表达式;循环执行表达式){
	循环体;
}

它的运行过程为

1. 首先，执行循环初始化表达式，这个只会执行一次！！
2. 然后，执行循环条件表达式，若值为真，则执行循环体，否则结束。
3. 接着执行循环体后执行之循环执行表达式。
4. 重复执行2、3直到2为假跳出循环。
   

2.简单应用

下面的程序演示了一个简单的1+2+…+n的值求解

int sumNums(int n){             // 入口函数传参为n
   int i;                      // 声明一个变量
   int sum = 0;                // 作为返回的值初始化为0
   for(i = 1; i <= n; ++i) {   // 循环
       sum += i;               // 循环体
   }
   return sum;                 // 返回结果
}

3.初始化表达式

3.1 初始化表达式外置

这里就是讲初始化表达式提到for循环外面

int sumNums(int n){             // 入口函数传参为n
   int i = 1;                      // 声明一个变量
   int sum = 0;                // 作为返回的值初始化为0
   for(; i <= n; ++i) {   // 循环
       sum += i;               // 循环体
   }
   return sum;                 // 返回结果
}

3.2 初始化表达式内置

这里就是可以直接进行初始化和赋值。但是这样使用for循环执行完之后会直接进行销毁变量。所以这个程序是错的！！！

int sumNums(int n){             // 入口函数传参为n
   for(int i = 1, sum = 0; i <= n; ++i) {   // 循环
       sum += i;               // 循环体
   }
   return sum;                 // 返回结果
}

3.3 初始化表达式的正确用法

为了之后还能使用变量，就需要在外面声明。

int sumNums(int n){             // 入口函数传参为n
   int i,sum;
   for(i = 1, sum = 0; i <= n; ++i) {   // 循环
       sum += i;               // 循环体
   }
   return sum;                 // 返回结果
}

4.条件表达式

条件表达式可以省略，但是会是个死循环，下面的程序必超时。

int sumNums(int n){             // 入口函数传参为n
   int i = 1;                      // 声明一个变量
   int sum = 0;                // 作为返回的值初始化为0
   for(;; ++i) {   // 循环
       sum += i;               // 循环体
   }
   return sum;                 // 返回结果
}

5.执行表达式

它是结构体执行完之后加的一部分内容，本身可以放在循环体内。

int sumNums(int n){             // 入口函数传参为n
   int i = 1;                      // 声明一个变量
   int sum = 0;                // 作为返回的值初始化为0
   for(;i<= n; ) {   // 循环
       sum += i;               // 循环体
       i++;
   }
   return sum;                 // 返回结果
}

---

课后习题

剑指 Offer 64. 求1+2+…+n

剑指 Offer 64. 求1+2+…+n
题目描述

求1+2+...+n，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

思路1

管那么多，循环冲！不解释，知识点有。

int sumNums(int n){           
    int i;                      
    int sum = 0;               
    for(i = 1; i <= n; ++i) {   
        sum += i;              
    }
    return sum;                
}

思路2

没限制递归呀。递归冲！

int sumNums(int n){
    if(n == 1) return 1;//递归出口
    return n + sumNums(n - 1); //下一层递归
}

---

231. 2 的幂

231. 2 的幂
题目描述

给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。
如果存在一个整数 x 使得 n == 2x ，则认为 n 是 2 的幂次方。

思路1

同样的循环冲就好了，但是要注意溢出问题。

bool isPowerOfTwo(int n){
    for(int i = 1;i <= 1<<30;){
        if(i == n)  return true;
        if(i == 1<<30) break;	//防止溢出
        else i*=2;
    }
    return false;
}

思路2

其实溢出也是假溢出 把i变成unsigned 就会很省事

bool isPowerOfTwo(int n){
    for(unsigned int i = 1;i <= 1<<30;i*=2){
        if(i == n)  return true;
    }
    return false;
}

思路3

高级用法之位运算，之位与
因为2的幂在二进制表示中就是只有一个1其它都是0 所以用x&(x-1) == 0 判断是不是就好了
看不懂请跳过0.0

bool isPowerOfTwo(int n){
    return n<=0?0:!(n & (n-1));
}

---

326. 3 的幂

326. 3 的幂
题目描述

给定一个整数，写一个函数来判断它是否是 3 的幂次方。如果是，返回 true ；否则，返回 false 。
整数 n 是 3 的幂次方需满足：存在整数 x 使得 n == 3x

思路

其实和上面差不多 我们这次换个思路，3的幂肯定是除了1只包含3这个质因子，我们不断的除3看是否最后是1就好了。

bool isPowerOfThree(int n){
    if(n <= 0) return false;
    while(n % 3 == 0) n /= 3;
    if(n == 1) return true;
    return false;
}

---

342. 4的幂

342. 4的幂
题目描述

给定一个整数，写一个函数来判断它是否是 3 的幂次方。如果是，返回 true ；否则，返回 false 。
整数 n 是 3 的幂次方需满足：存在整数 x 使得 n == 3x

思路

和3的幂是一样的。

bool isPowerOfFour(int n){
    if(n <= 0) return false;
    while(n % 4 == 0)	//判断能否整除
        n /= 4;		//除4
    return n == 1;
}

---

1492. n 的第 k 个因子

1492. n 的第 k 个因子
题目描述

给你两个正整数 n 和 k 。
如果正整数 i 满足 n % i == 0 ，那么我们就说正整数 i 是整数 n 的因子。
考虑整数 n 的所有因子，将它们 升序排列 。请你返回第 k 个因子。如果 n 的因子数少于 k ，请你返回 -1 。

思路

直接去统计是否到达第k个因子就好了。

int kthFactor(int n, int k){
        for(int i = 1; i <= n ; i++){
            if(n % i == 0) k--;
            if(!k) return i;
        }
        return -1;	//最后k都还有数字
}

---

367. 有效的完全平方数

367. 有效的完全平方数
题目描述

给定一个 正整数 num ，编写一个函数，如果 num 是一个完全平方数，则返回 true ，否则返回 false 。
进阶：不要 使用任何内置的库函数，如 sqrt 。

思路1

直接去遍历查找就完事了。

int isPerfectSquare(int x){
    int i;
    long long p;
    for(i = 1; ; ++i) {    
        p = (long long)i*i;  
        if(p == x) {
            return true;     
        } 
        if(p > x) {
            return false;
        }
    }
    return false;         
}

思路2

为了加速二分查找。

bool isPerfectSquare(int num){
    unsigned int left = 0, right = 1<<16;//最大也就这么大了
    while(left < right){
        unsigned int mid = left + (right - left)/2;
        if(mid * mid > num) right = mid;
        else if(mid *mid == num) return true;
        else left = mid + 1;
    }
    return false;
}

写在最后
今天完成了第二天的打卡，算法笔记因为第二章内容很简单，我想跳过，但是内容还是有亿点点多，我晚上肯定能更完-.-希望大家可以跟我一起。0.0