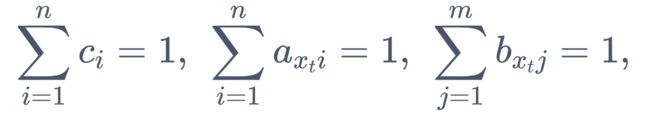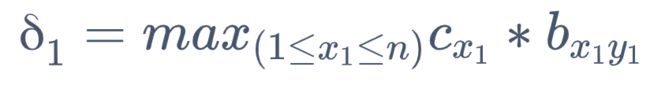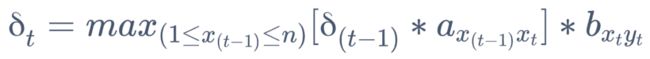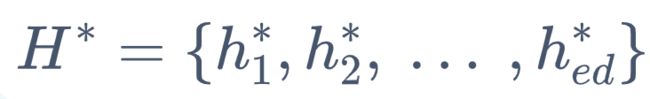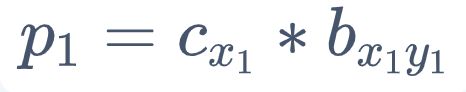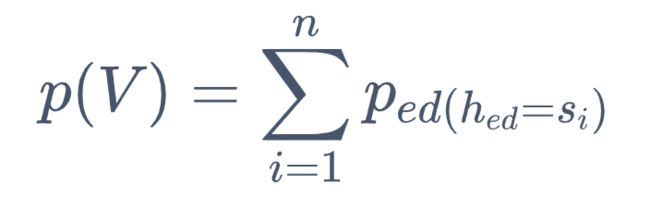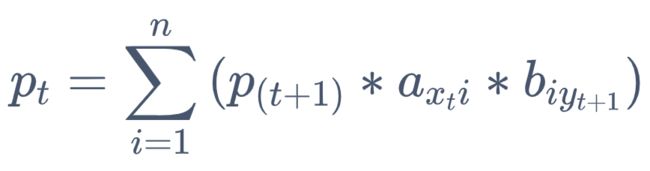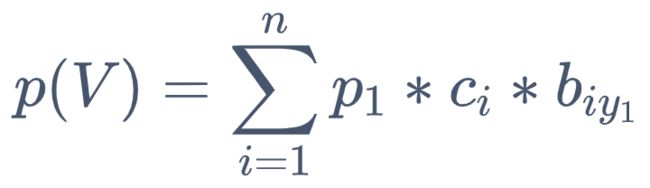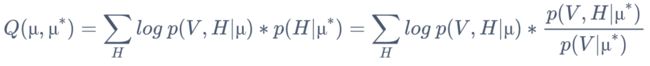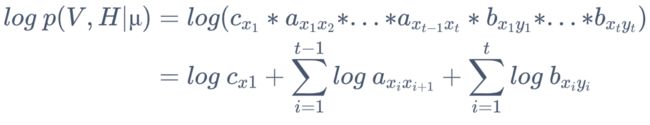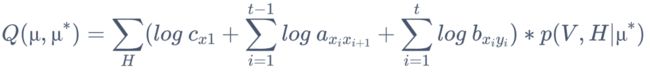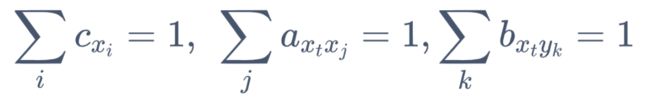尽量以最少的符号去诠释模型,对公式推导的每个步骤也会详细解读,因为是按自己的思路理解的,所以符号应用上会与网上常见教程有出入。
一、定义模型
一个隐马尔可夫模型(Hidden Markov Model, HMM)包含以下概念和参数:
- 按一定概率生成不可观测的隐含状态序列 H 链;
- 由各个隐含状态生成一个可观测结果序列 V 链;
- H 之间存在一个状态转换概率函数矩阵 A;
- H 到 V 存在一个映射概率函数矩阵 B;
- H 的初始状态生成概率变量 C;
- S 为所有隐含状态的集合,有 n 种可能的状态;
- R 为所有可观测结果的集合,有 m 种可能的结果;
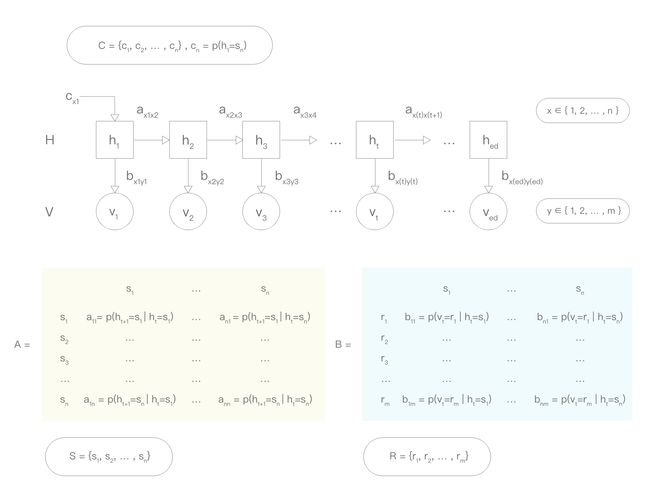
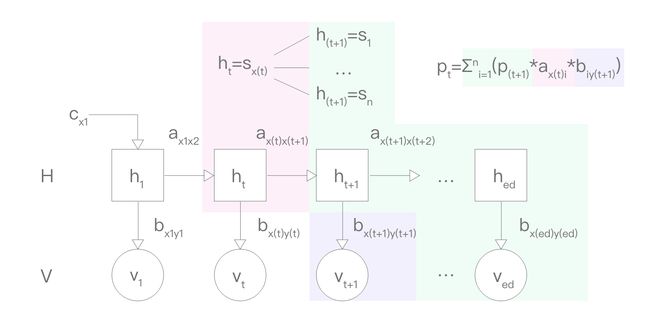
下图为包含以上参数的可视化模型:
用实际的例子套用的话,可以用自然语言处理里的词性标注做例子,这也是 HMM 比较常见的应用。
在词性标注中,把实际词语序列(一个句子)看作 V 链,把对应的词性标注序列看作 H 链。
比如
I watched the play last night.
是一条 V 链,对应的 H 链即为:
(代词-动词-限定词-名词-形容词-名词)
c(x1) 即为 “代词出现的概率”;
b(x1y1) 即为 “在出现代词的情况下,出现单词 'I' 的概率”;
a(x1x2) 即为 “在出现代词的情况下,下一个出现的单词为动词的概率”;
在没给定句子的原始模型中,x 和 y 都是变量,分别有 n 种和 m 种可能。
另外,HMM 有以下几个约束条件:
根据马尔可夫性假设:H 链在任一时刻 t 的状态只依赖于其前一个时刻的状态。可得 a 之间没有依赖关系。
根据观测独立性假设:任意时刻 t 的观测结果 v(t),只依赖于该时刻的隐含状态 h(t)。可得 b 之间没有依赖关系。
-
所有的初始状态概率和为1;
某时刻 t 的隐含状态转移到一下个所有可能的状态的概率和为1;
某时刻 t 的隐含状态观测到的所有可能的观测值的概率和为1。转化为公式即:
二、HMM 解决的主要问题
- 给出观测序列 V 和模型 μ=(A, B, C),选择出最好解释 V 的对应的隐含状态序列 H;(可应用于词性标注)
- 给出模型 μ,算出某个观测序列发生的概率 p(V);
- 给定观测序列 V,计算模型 μ 的参数 (A, B, C) 以最好解释 V。
问题一:给出观测序列 V 和模型 μ,选择出最好解释 V 的对应的隐含状态序列 H
回到词语标注的例子,把实际词语序列(一个句子)看作 V 链,把对应的词性标注序列看作 H 链。一般实际情况为,有一个语料库,包含很多需要标注词性的句子。所以问题二可转换成给一个句子的每个单词计算出最有可能的词性进行标注。
可以用 Viterbi 算法实现:
设 δ(t) 表示在 t 时刻、状态 h(t)=s(xt) 的序列概率最大值
1. 初始值
2. 推导过程
解析:在确认 t-1 时刻的最大概率的基础上,h(t-1) 会有 n 种可能状态,取其中转换到 ht 的概率最大的一项求积,再进行对应的 b 转换。
当取到最大值时,记 h(t)* 为相应的状态值。
3. 到最后一项,求得整条 V 链最佳路径的概率
当取到最大值时,记 h(ed)* 为相应的状态值。
4. 对最优路径 H 进行回溯,即为所求词性序列
问题二:给出模型 μ=(A, B, C),算出某个观测序列发生的概率 p(V)
遍历算法(蛮力算法)
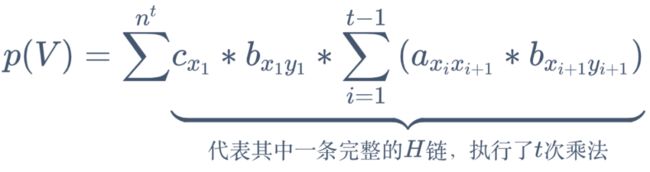
基本思路,计算出每一条能生成对应 V 链的 H 链的概率,然后累加起来。有以下公式:
累加 n^t 次,是因为一条 H 链中,每个转换的节点都有 n 种转换组合,然后有 t 个节点。
这种算法非常耗时,计算复杂度是 O(tn^t) 指数幂级别,一般不采用。
前向算法(Forward Algorithm)
基本思路:运用动态规划的思想,把每一个节点生成的概率先确定,然后再以此为基础计算生成下一个节点的概率。
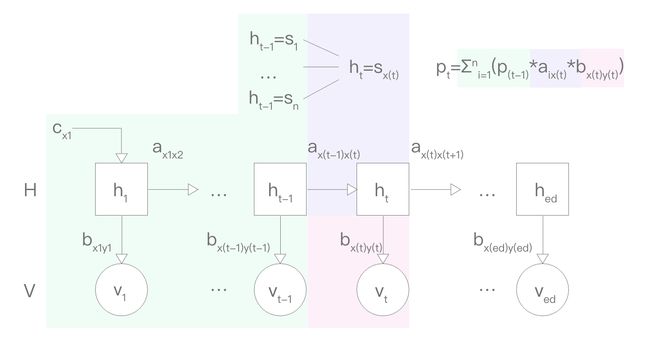
1. 初始概率
p(t) 表示在 t 时刻、状态 h(t)=s(xt) 的概率
2. 每次转换的推导
p(t) 为得出前 (t-1) 个观察值的概率,但对应的 h(t-1) 有 n 种可能,把 x(t-1) 视为变量。
对每一种 ht,h(t+1) 只取某一种对应的可能,最后乘对应的一种 b 转换。一次转换进行了 n^2 次运算。下图为可视化解析:
3. 到最后一步,由于不需要再做转换,只需要 把 n 种 h(ed) 的概率相加即可
每个节点都进行了 n*n 次运算,共有 t 个节点,所以计算复杂度为O(tn^2),下面的后向算法同理。
后向算法(Backward Algorithm)
基本思路:与前向算法一样采用动态规划思想,从最后一项开始。
1. 初始概率
p(ed)=1
因为后向算法是由时刻 t+1 的概率值推算出时刻 t 的概率,最后一项没有任何因素需要依赖,所以概率为1(100%)
2. 每次推导的转换
这里的 p(t) 指得出从 (t+1) 项到最后一项观察值的概率,h(t+1) 有 n 种可能,把 x(t+1) 视为变量,而 ht 取对应的1种可能,最后乘对应的一种 b 转换。这一次转换进行了 n^2 次运算。下图为可视化解析:
3. 最后推导到最前
可以理解为 t=0 时,求得目标概率
问题三:给定观测序列 V,计算模型 μ 的参数 (A, B, C) 以最好解释 V
这种应用属于无监督学习,可使用 Baum-Welch 算法(本质上是 EM 算法),本质上是要求对数似然函数:log p(V, H | μ)。
(到目前 EM 算法和拉格朗日乘子法还没完全搞懂,所以直接写下计算过程)
1. 根据 EM 算法列出 Q 函数
其中 μ* 是模型当前估算值,一开始先预设一个,μ 是最终要求的模型最值
因为 p(V | μ*) 是可确定的值,等式中的分母可省略。
2. 解似然函数
3. 代入到 Q 函数
4. 上一步的3个加项拆开,三个部分分别满足以下约束条件
- 最后分别对这三个部分根据约束依次利用 拉格朗日乘子法 求解,即可求解得到模型的参数。
最后一个小彩蛋