《数据结构与算法分析：C语言描述》复习——第十章“算法设计技巧”——Huffman编码

2014.07.06 16:47

简介：

　　给定一段有固定符号集合S构成的文本T，集合S中总共有n种符号。如果对于每种符号，使用一种不同的由‘0’和‘1’构成的位字符串来代替，比如：

　　　　‘a’->‘01’

　　　　‘c’->'101'

　　　　'd'->‘11’

　　　　...

　　例如，文本“acd”经过这种编码就变成了“0110111”。

　　这样，就可以把文本T中的符号全部替换为‘0’‘1’构成的二进制串，这样就能以二进制文件的形式保存信息了。并且，一个ASCII字符默认占用一个字节，也就是8位。但使用这种不定长的编码方式一个字符占用的位数可能小于8位，于是可能达到压缩数据的效果。Huffman编码的规则，就是通过选定合适的编码，使得这段文本经过编码转换后的二进制串的长度最短。

图示：

　　用算法描述Huffman编码的过程还是比较简单的：

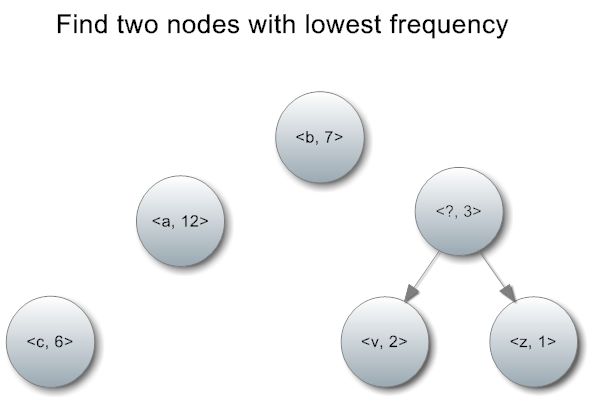
　　1. 定义键值对<字符, 出现频率>，比如<a, 12>表示a字符出现了12次。

　　

　　2. 每次选出出现频率最低的两个字符，组合成一个字符（字符当然不能组合，但频率是可以相加的），重新放入候选集中。

　　

　　3. 这个组合的过程，其实就是构建二叉树的过程

　　

　　新结点的频率等于两个子节点的频率之和，而新节点上对应的字符没有实际意义，所以我们姑且标记为‘?’。

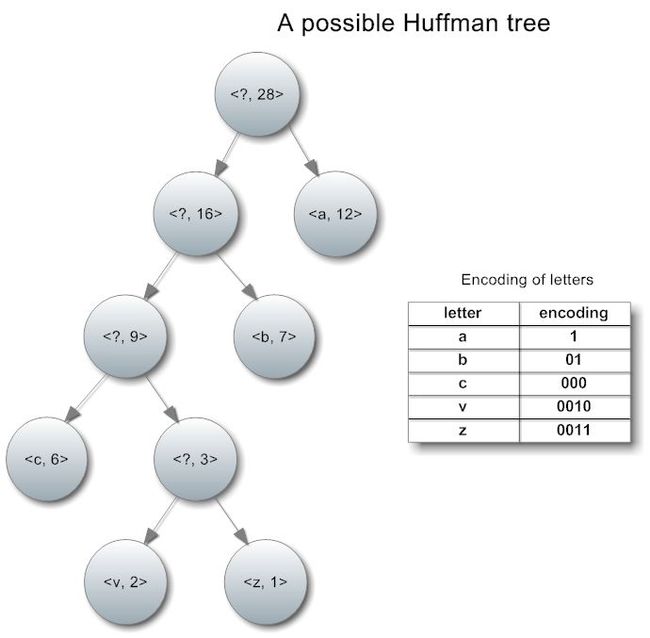
　　每经过一轮这样的操作，我们取出两个结点，放回一个结点，所以要经过n-1轮才能得到一棵完整的树，比如这样：

　　

　　上图中给出了这棵树对应的字符编码方式，其实每个字符的编码对应于从根结点到叶结点的路径，‘0’向左，‘1’向右。

　　由于组合两个结点时，左右次序可以调换，因此同一套文本与字符可以构建出2^(n-1)种的Huffman树。任何一种的效果都是相同的，目的只有一个：压缩数据。

　　如何每次选出最小的两个呢？最小堆。

　　问题是：为什么每次选出最小的，结果就是最好的呢？贪婪。

实现：

  1 // A simple illustration for 
  2 #include <iostream>
  3 #include <queue>
  4 #include <string>
  5 #include <unordered_map>
  6 #include <vector>
  7 using namespace std;
  8 
  9 // The character statistics type
 10 typedef unordered_map<char, int> StatType;
 11 // The character encoding type
 12 typedef unordered_map<char, string> EncodeType;
 13 
 14 struct TreeNode {
 15     char ch;
 16     int weight;
 17     TreeNode *left;
 18     TreeNode *right;
 19     
 20     TreeNode(char _ch, int _weight): ch(_ch), weight(_weight), 
 21         left(nullptr), right(nullptr) {}
 22 };
 23 
 24 struct GreaterFunctor {
 25     bool operator () (const TreeNode *x, const TreeNode *y) {
 26         return x->weight > y->weight;
 27     }
 28 };
 29 
 30 void deleteTree(TreeNode *&root)
 31 {
 32     if (root == nullptr) {
 33         return;
 34     } else {
 35         deleteTree(root->left);
 36         deleteTree(root->right);
 37         delete root;
 38         root = nullptr;
 39     }
 40 }
 41 
 42 void calculateEncoding(const TreeNode *root, EncodeType &encoding, string &path)
 43 {
 44     if (root == nullptr) {
 45         return;
 46     }
 47     
 48     if (root->ch != '\0') {
 49         encoding[root->ch] = path;
 50         return;
 51     }
 52     
 53     path.push_back('0');
 54     calculateEncoding(root->left, encoding, path);
 55     path.pop_back();
 56     
 57     path.push_back('1');
 58     calculateEncoding(root->right, encoding, path);
 59     path.pop_back();
 60 }
 61 
 62 void huffmanEncoding(const StatType &statistics, EncodeType &encoding)
 63 {
 64     priority_queue<TreeNode *, vector<TreeNode *>, GreaterFunctor> pq;
 65     
 66     int n;
 67     
 68     n = 0;
 69     for (StatType::const_iterator sta_it = statistics.begin(); 
 70         sta_it != statistics.end(); ++sta_it) {
 71         pq.push(new TreeNode(sta_it->first, sta_it->second));
 72         ++n;
 73     }
 74     
 75     TreeNode *p1, *p2, *p3;
 76     int i;
 77     for (i = 0; i < n - 1; ++i) {
 78         p1 = pq.top();
 79         pq.pop();
 80         p2 = pq.top();
 81         pq.pop();
 82         
 83         p3 = new TreeNode('\0', p1->weight + p2->weight);
 84         p3->left = p1;
 85         p3->right = p2;
 86         pq.push(p3);
 87     }
 88     
 89     TreeNode *root = pq.top();
 90     pq.pop();
 91     
 92     string code = "";
 93     calculateEncoding(root, encoding, code);
 94     deleteTree(root);
 95 }
 96 
 97 int main()
 98 {
 99     int i, n;
100     string s;
101     int weight;
102     StatType statistics;
103     EncodeType encoding;
104     
105     while (cin >> n && n > 0) {
106         for (i = 0; i < n; ++i) {
107             cin >> s >> weight;
108             statistics[s[0]] = weight;
109         }
110         huffmanEncoding(statistics, encoding);
111         
112         for (EncodeType::const_iterator enc_it = encoding.begin(); 
113             enc_it != encoding.end(); ++enc_it) {
114             cout << enc_it->first << ':' << enc_it->second << endl;
115         }
116         cout << endl;
117 
118         statistics.clear();
119         encoding.clear();
120     }
121     
122     return 0;
123 }