自定义view-手撸一个饼图

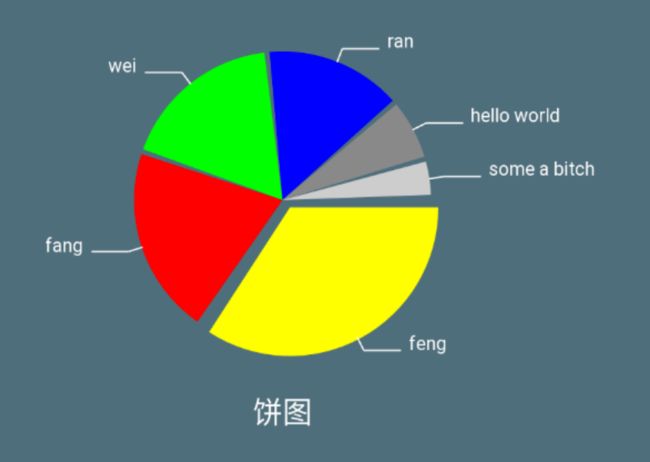
1、饼图可以应用在多方面，比如 财务类资金用途占比统计、生活类个人喜好占比、等等，待产品提出这样得效果，我们可以随意的绘制出来。下面我来一步步剖析饼图的绘制过程。如下图先看效果

image.png

2、第一步先分析一下这个饼图的思路，首先这个饼图是由多个扇形以及折线以及文字组成。可以分为三块来分别绘制。首先需要用到的知识点先大概说一下。

· 画扇形用到canvas.drawArc()或者用Path类下的path.arcTo() 都可以实现
· 画折线用drawLine()即可
· 画文字用drawText()即可
· 计算弧长上的坐标需要用到三角函数 cos 余弦、 sin正弦

3、我们直接来分析代码

/**
 * 饼图的颜色
 */
private int[] mColors = {Color.YELLOW, Color.RED, Color.GREEN, Color.BLUE, Color.GRAY, Color.LTGRAY};
/**
 * 初始化各个扇形的角度
 */
private float[] mPieAngles = {123, 73, 63, 53, 23, 13};
/**
 * 初始化文字
 */
private String[] texts = {"feng", "fang", "wei", "ran", "hello world", "some a bitch"};

/**
 * 扇形最大的间隔度数
 */
private int angleDash = 2;

/**
 * 扇形的半径
 */
private int mRadius = 200;

以上是该饼图所需要的一些初始化数据

4、先计算出view可用的宽和高方便平移坐标系，以及初始化扇形的外框矩形坐标

@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
    super.onSizeChanged(w, h, oldw, oldh);
    //view 的可用高度
    mViewHeight = h - getPaddingTop() - getPaddingBottom();
    //view 的可用宽度
    mViewWidth = w - getPaddingLeft() - getPaddingRight();
    //画扇形的矩形坐标
    mRectF = new RectF(-mRadius, -mRadius, mRadius, mRadius);
}

5、之后我们需要初始化扇形、折线、文字的画笔，以及坐标系原点

  private void init() {
    //扇形的画笔
    mPiePaint = new Paint();
    mPiePaint.setAntiAlias(true);
    mPiepath = new Path();
    //折线的画笔
    mLinePaint = new Paint();
    mLinePaint.setStrokeWidth(2);
    mLinePaint.setColor(Color.WHITE);
    mLinePaint.setAntiAlias(true);
    //文字的画笔
    mTextPaint = new Paint();
    mTextPaint.setAntiAlias(true);
    mTextPaint.setColor(Color.WHITE);
    mTextPaint.setTextSize(25);
    //标题的画笔
    mTitlePaint = new Paint();
    mTitlePaint.setTextSize(40);
    mTitlePaint.setAntiAlias(true);
    mTitlePaint.setTextAlign(Paint.Align.CENTER);
    mTitlePaint.setColor(Color.WHITE);
}

@Override
protected void onDraw(Canvas canvas) {
    super.onDraw(canvas);
    //将坐标原点平移到(mViewWidth / 2, mViewHeight / 2)位置处
    canvas.translate(mViewWidth / 2, mViewHeight / 2);
    //画文字和折线以及扇形
    drawPieAndLineAndText(canvas);
    //画标题
    drawTitle(canvas);
}

说明：将坐标系平移到view中心 便于之后的弧长的中点坐标的计算，下面正式进入核心代码

6、画扇形

private void drawPie(Canvas canvas, int i) {
    //画扇形
    if (i == 0) {
        mPiepath.moveTo(10, 10);
        mPiepath.arcTo(new RectF(mRectF.left + 10, mRectF.top + 10,
                mRectF.right + 10, mRectF.bottom + 10), startAngle, mPieAngles[i]);
    } else {
        mPiepath.moveTo(0, 0);
        mPiepath.arcTo(mRectF, startAngle, mPieAngles[i]);
    }
    mPiePaint.setColor(mColors[i]);
    canvas.drawPath(mPiepath, mPiePaint);
    mPiepath.reset();
    startAngle = (int) (startAngle + mPieAngles[i] + angleDash);
}

这里我需要解释一下，图示效果，有一个弧度最大的扇形有一个偏移效果，我这边是将path的起点坐标从原来的（0，0）变为（10，10），将该扇形的矩形轮廓坐标也对应的偏移了10个像素，即可达到偏移效果
这里的startAngle是每个扇形的起始绘制的角度，每绘制一个扇形，下一个扇形的起始绘制角度就是 上一个扇形的角度与上一个扇形的起始的角度以及扇形之间的间隔角度和。

7、画折线和文字 这里只贴出核心代码解释

        float xStart = (float) (mRadius * Math.cos(Math.toRadians(startAngle - angleDash - mPieAngles[i] / 2)));
        float yStart = (float) (mRadius * Math.sin(Math.toRadians(startAngle - angleDash - mPieAngles[i] / 2)));
        float xStop = (float) ((mRadius + lineFirstLength) * Math.cos(Math.toRadians(startAngle - angleDash - mPieAngles[i] / 2)));
        float yStop = (float) ((mRadius + lineFirstLength) * Math.sin(Math.toRadians(startAngle - angleDash - mPieAngles[i] / 2)));
        canvas.drawLine(xStart, yStart, xStop, yStop, mLinePaint);
        if (xStop > xStart) {
            canvas.drawLine(xStop, yStop, xStop + lineSecondLength, yStop, mLinePaint);
            mTextPaint.setTextAlign(Paint.Align.LEFT);
            canvas.drawText(texts[i], xStop + lineSecondLength + 10, yStop, mTextPaint);
        } else {
            canvas.drawLine(xStop, yStop, xStop - lineSecondLength, yStop, mLinePaint);
            mTextPaint.setTextAlign(Paint.Align.RIGHT);
            canvas.drawText(texts[i], xStop - lineSecondLength - 10, yStop, mTextPaint);
        }

根据三角函数很容易计算出，每个扇形的弧长中点坐标 即上面的xStart,yStart 然后根据同样的算法，将半径延长即可计算出第一段线段的终点坐标 即 xStop，yStop,根据这两个点即可画出第一段线段。

第二段线段就需要做一些判断了 根据第一段线段的走向，判断出第二段线段的走势，如何第一段是趋于向右的，那么第二段线段水平向右，反之向左。

画完两段线段之后再末尾 绘制对应的文字 （这里根据画笔paint的一个属性即可确定文字是从左向右还是从右向左）
mTextPaint.setTextAlign(Paint.Align.LEFT);

到此，简单的饼图就绘制完成了，其中主要弧长中点坐标的计算，以及三角函数和android的drawXXX()方法的结合使用

源码github地址：https://github.com/weiranqiaobo/pieDemo/tree/master