【Android春招每日一练】（三十四） LeetCode Hot 5题+总结（完）

概览

LeetCode Hot：和为 K 的子数组、最短无序连续子数组、合并二叉树、回文子串、每日温度

LeetCode Hot

2.91 和为 K 的子数组

给你一个整数数组 nums 和一个整数 k ，请你统计并返回该数组中和为 k 的连续子数组的个数。

示例 1：
输入：nums = [1,1,1], k = 2
输出：2

//前缀和
class Solution {
    public int subarraySum(int[] nums, int k) {
        // 记录合适的连续字符串数量
        int count=0;
        // 记录前面数字相加之和
        int pre=0;
        // map记录前几个数字之和为key，出现相同和的次数为value
        HashMap<Integer,Integer> map = new HashMap<>();
        // 初始化
        map.put(0,1);
        for (int i = 0; i < nums.length; i++) {
            pre+= nums[i];  // 前缀和
            // 设
            // pre[i]=pre[i−1]+nums[i]
            // 由于补上了0，1这个情况 问题由多少个连续数字之和等于k 转为
            // pre[i]−pre[j−1]==k （前缀和之差为k，代表这两个前缀和中间的数字相加就是K）
            // 如果前面某些数字之和加上这个数字正好等于K（存在一个数字加上nums[i]结果为K
            // 说明找到了
            if (map.containsKey(pre-k)){
                // 累计
                count+=map.get(pre-k);
            }
            // 计算新的和放入map
            map.put(pre,map.getOrDefault(pre,0)+1);
        }
        return count;
    }
}

2.92 最短无序连续子数组

给你一个整数数组 nums ，你需要找出一个 连续子数组 ，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。

请你找出符合题意的 最短 子数组，并输出它的长度。

示例 1：

输入：nums = [2,6,4,8,10,9,15]
输出：5
解释：你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。

/*
我们可以假设把这个数组分成三段，左段和右段是标准的升序数组，中段数组虽是无序的，但满足最小值大于左段的最大值，最大值小于右段的最小值。
那么我们目标就很明确了，找中段的左右边界，我们分别定义为begin 和 end;
分两头开始遍历:

从左到右维护一个最大值max,在进入右段之前，那么遍历到的nums[i]都是小于max的，我们要求的end就是遍历中最后一个小于max元素的位置；
同理，从右到左维护一个最小值min，在进入左段之前，那么遍历到的nums[i]也都是大于min的，要求的begin也就是最后一个大于min元素的位置。
*/
//带入题目数组模拟一下
class Solution {
    public int findUnsortedSubarray(int[] nums) {
        //初始化
        int len = nums.length;
        int min = nums[len-1];
        int max = nums[0];
        int begin = 0, end = -1;	//初始化为-1，保证原数组升序时返回0
        //遍历
        for(int i = 0; i < len; i++){
            if(nums[i] < max){      //从左到右维持最大值，寻找右边界end
                end = i;
            }else{
                max = nums[i];
            }
            if(nums[len-i-1] > min){    //从右到左维持最小值，寻找左边界begin
                begin = len-i-1;
            }else{
                min = nums[len-i-1];
            }            
        }
        return end-begin+1;
    }
}

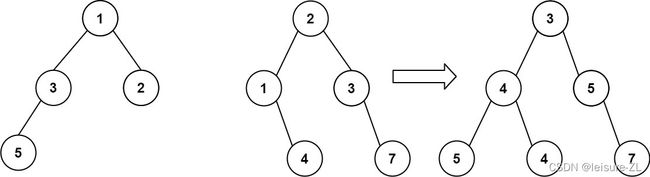
2.93 合并二叉树

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

//DFS
class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1 == null){
            return root2;
        }
        if(root2 == null){
            return root1;
        }
        TreeNode merged = new TreeNode(root1.val + root2.val);	//构建新的节点，相当于重新生成一棵树
        merged.left = mergeTrees(root1.left,root2.left);
        merged.right = mergeTrees(root1.right,root2.right);
        return merged;
    }
}

2.94 回文子串

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

输入：s = "abc"
输出：3
解释：三个回文子串: "a", "b", "c"

class Solution {
    public int countSubstrings(String s) {
        // 中心扩展法
        int ans = 0;
        for (int center = 0; center < 2 * s.length() - 1; center++) {
            // left和right指针和中心点的关系是？
            // 首先是left，有一个很明显的2倍关系的存在，其次是right，可能和left指向同一个（偶数时），也可能往后移动一个（奇数）
            // 大致的关系出来了，可以选择带两个特殊例子进去看看是否满足。
            int left = center / 2;
            int right = left + center % 2;

            while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
                ans++;
                left--;
                right++;
            }
        }
        return ans;
    }
}

2.95 每日温度

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指在第 i 天之后，才会有更高的温度。如果气温在这之后都不会升高，请在该位置用 0 来代替。

示例 1:

输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

/**
 * 最简单莫过于双重循环，笔试时至少不会丢分
 */
public int[] dailyTemperatures(int[] T) {
    int[] res = new int[T.length];
    for (int i = 0; i < T.length - 1; i++) {
        for (int j =  i + 1; j < T.length; j++) {
            if (T[j] > T[i]) {
                res[i] = j - i;
                break;
            }
        }
    }
    return res;
}

/**
 * 根据题意，从最后一天推到第一天，这样会简单很多。因为最后一天显然不会再有升高的可能，结果直接为0。
 * 再看倒数第二天的温度，如果比倒数第一天低，那么答案显然为1，如果比倒数第一天高，又因为倒数第一天
 * 对应的结果为0，即表示之后不会再升高，所以倒数第二天的结果也应该为0。
 * 自此我们容易观察出规律，要求出第i天对应的结果，只需要知道第i+1天对应的结果就可以：
 * - 若T[i] < T[i+1]，那么res[i]=1；
 * - 若T[i] > T[i+1]
 *   - res[i+1]=0，那么res[i]=0;
 *   - res[i+1]!=0，那就比较T[i]和T[i+1+res[i+1]]（即将第i天的温度与比第i+1天大的那天的温度进行比较）
 */
public int[] dailyTemperatures(int[] T) {
    int[] res = new int[T.length];
    res[T.length - 1] = 0;
    for (int i = T.length - 2; i >= 0; i--) {
        for (int j = i + 1; j < T.length; j += res[j]) {
            if (T[i] < T[j]) {
                res[i] = j - i;
                break;
            } else if (res[j] == 0) {
                res[i] = 0;
                break;
            }
        }
    }
    return res;
}

总结

1.刷完今天最后5题，LeetCode的刷题之旅也告一段落，100题中有些非常偏、不易理解或者需要会员的题就没有记录了，加上剑指offer总共可能有150道左右，也总结了一些方法，模板套路；
2.本系列记录了寒假每日刷题，总结知识点的过程，总共学习34天，我感觉还是收获颇丰，至少在后面面试的时候不至于没有把握，至少心里有底；
3.春招金三银四，我对自己的规划是至少在三月份之前，需要把前面所有知识牢记，150多道算法理解、记熟，然后牛客面经，面试模拟等同步进行，准备开始投递简历；
4.最后，这一个多月的整理笔记已经放到我的GitHub上，有需要的可以免费下载：
https://github.com/Leisure-ZL/MarkDownDoc.git
Algorithm.pdf（算法）、Recruitment.pdf（知识点）
注：算法解析来自官方题解、各路大神的题解和自己的解析等，因为来源太多，就不一一@了，如有侵权请联系删除；知识点大多来自各个博客文章和书籍整理，如有侵权请联系删除。