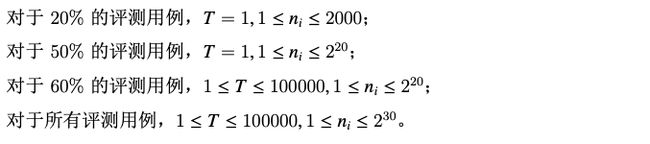第十二届蓝桥杯B组国赛真题详解及考点总结
试题A:
考点:计算机网络
答案:25
题解:
200M的带宽理论下载速率为1024×200÷8=25600KB/s=25M/s
1Mbps代表每秒传输1, 000, 000位(bit),即每秒传输的数据量为:1, 000, 000/8 Byte,即125, 000Byte/s = 125KB/s
200Mbps = 200 * 125KB/s = 25, 000 KB/s = 25 MB/s
试题B:
考点:数位截取、质数筛
答案:1903
题解:
一位的质数为2,3,5,7,对于一个数字的每一位判断是否为上面4个数字之一,且它本身是不是质数,可以先预处理出1-20210605中所有质数,这一块需要用质数筛做这,当然也可以直接暴力找就是时间需要比较长(可能比赛结束也跑不出来),然后在累计是质数且每一位都是质数的数即可,总数据量很小,直接暴力循环判断即可。
#include试题C:
考点:模拟、日期
答案:977
题解:
日期也是蓝桥杯最最最频繁的考点了,只要注意一下闰年,然后暴力循环即可,判断完全平方数我们可以看出一共8位数那所有数的和不超过72,至多为8的平方,把1-8的平方预处理出来然后枚举每一天即可,。
解法1
Excel处理数据,由于可能自己模拟时间的时候会出错,所以可以从Excel得到所有日期,储存到记事本中,然后借助c++程序进行判断是否为完全平方数即可。

#include解法2
思路一致不过是直接在程序中模拟日期。
/**977**/
#include 试题D:
考点:动态规划、递归转递推
答案:2653631372
题解:
很明显递归直接求解会超时,那我们就转换思路,递归转递推,我们需要求得是有2021个节点的二叉树值最小,那我们dp[i]就设为有i个节点的二叉树最小值,然后我们状态改如何转移呢,当多一个节点作为父节点时,我们只需要考虑左右子树节点个数的搭配从中取个最小值即可,所以枚举左子树节点个数,右子树节点个数为i-j-1,然后根据上面的权值方程进行赋值即可。
#include试题E:
考点:字符串处理
题解:
签到送分题,c可以用toupper 或者直接减去32 c++中有transform
#include
cout << str << endl;
}
试题F:
考点:预处理、前缀和、二分
题解:
解法1
很容易想到用前缀和来处理[l,r]的区间和,那么有个问题就是l,r数据过大直接预处理整个区间会爆空间,那我们来考虑如何来压缩空间
首先将数列分层
1
1 2
1 2 3
1 2 3 4
我们会发现第i层数的数的个数为i,其和为 ( 1 + i ) ∗ i / 2 (1+i)*i/2 (1+i)∗i/2数的总数为1e12,那么用1e7层就可以存下所有的前缀和,具体的做法是,前缀和记录1-n层的值,先找到具体在哪一层(x),然后值就为x-1层的值+多出来的数的值,多出来多少个的值也是也是一个等差数列 ( n + 1 ) ∗ n / 2 (n+1)*n/2 (n+1)∗n/2
(参考博客)
估计层数 – (1+x)*x/ 2>=1e12 ==> x = 1500000层
所以1500000层可以容纳1e12个数,也可以用数组存下
关键公式:sum = 前缀和求ab中间层数的和 + a当前层后面几个数量 + b当前层前面几个数量
解决给定第n个数,求出他在第几层第几个数。
解决求中间层数
#include解法2
思路与解法1大致相同,做了两个优化。
优化1:发现每一层的数的值为 C 3 i + 2 C_{3}^{i+2} C3i+2
优化2:二分找在哪一层
根据前缀和得出区间之和为 s u m [ r ] − s u m [ l − 1 ] sum[r] - sum[l-1]sum[r]−sum[l−1]。
题目明显是分段来求的,具体来说是将序列看做 { 1 } , { 1 , 2 } , { 1 , 2 , 3 } , { 1 , 2 , 3 , 4 } , . . . \{1\},\{1,2\},\{1,2,3\}, \{1,2,3,4\},...{1},{1,2},{1,2,3},{1,2,3,4},...
其中每一块的长度刚好是 1 , 2 , 3 , 4... 1,2,3,4...1,2,3,4...,而每一块的所有元素之和是 1 , 3 , 6 , 10... 1,3,6,10...1,3,6,10...,每块元素之和的前缀和为 p r e [ i ] = { 1 , 4 , 10 , 20... } pre[i] = \{1,4,10,20...\}pre[i]={1,4,10,20...},这个前缀和的第 i ii 项刚好对应了组合数 C i + 2 3 C_{i + 2}^3C
i+2
3
。
因此思路就很明确了,二分确定前面有多少个完整的块,然后 O ( 1 ) O(1)O(1) 算出这些块的和,最后拿 n nn 减去前面块的元素个数,得到的一定是一个新的块中的从1开始的连续若干个自然数,根据等差数列公式 n ( n + 1 ) 2 \frac{n(n + 1)}{2}
2
n(n+1)
即可求出,累加上述二者即可。
#include 试题G:
考点:找规律
题解:
随机打表后发现循环节为,求出来的循环节是大于等于n的最小的2的幂次,对t取余后暴力模拟。
#include试题H:
考点:数位DP
题解:(待补)
#include 试题I:
考点:线段树、二分
题解:
暂时补不动
参考博客
试题J:
考点:DP
题解:(待补)
(代码参考知乎)
#include
}
}
cout<<(dp[0][1][3] + dp[0][0][3]) * 6<<endl;
}
作者:蝴蝶结超人
链接:https://www.zhihu.com/question/458338964/answer/1931895214
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
总结
填空题比第12届省赛简单,大题前三道难度适中,后面三道有点难,线段树、数位dp还是知识盲区,压轴的dp暂时也搞不懂,要是有人搞懂了或者有看到详细的讲解可以私信我,感激不尽。