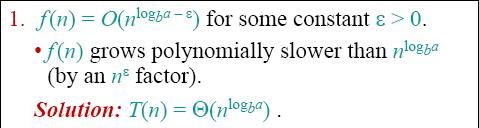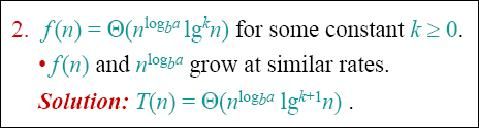note of introduction of Algorithms(Lecture 2)
Lecture 2
The lecture 2 is mainly about mathematical things, no algorithms. At the beginning of this class, teacher review those asymptotical annotations definition like Θ, ω, etc. Then, three methods to solving the recursive problems analysis such as subsititute method, recursion-tree method and master method has been given in turn.
honestly, I don't understood the content of this class completelly when I see this open class video.It's seems too abstractive to hold, may be a little boring:( i think. So, I read inrelated chapters(chapter 2, chapter 4)of the book(instruction of Algorithms) in chinese later and summarize this note.
- asymptotical annotation
big Θ: Θ(g(n)) = f(n); where n ≥ n0, 0 < c1*g(n) < f(n) < c2*g(n)
big Ο: O(g(n)) = f(n); where n ≥ n0, 0 < f(n) < c*g(n)
big Ω: Ω(g(n)) = f(n); for all n ≥ n0, 0 < c*g(n) < f(n)
Solving recurences
- subsititude method
the subsitude method has three general steps:
- Guess the form of the solution;
- verify by induction;
- solve for constants;
For examplt: T(n) = 4(T4/2) + n; Guess T(k) = c1*k2-c2*k
= 4(c1*(n/2)2-c2*(n/2)) + n
= c1*n2 - c2*n - (c2-1)*n; if c2 ≥ 1
- recursion-tree method
Recursion-tree methods models the costs of a recursive execution of an algorithm.
The recursion-tree methodexpress the recursive process as a tree, and the result of the recursive equals to the sum of the all nodes of this tree. See the following example:
- master method
The master method is used to resolve the recurrences the form like T(n) = a* T(n/b) + f(n) where a ≥ 1, b > 1, and f is asymptotically positive. The master method depends on tree common case(cont.) as follow:
For example:
T(n) = 4(Tn/2) +n
a = 4, b = 2 -> nlogba=n2; case 1:f(n) = O(n2-1) for ξ = 1;
So the common case 1 is applied, T(n) = Θ(n2)