机器学习笔记2——比较检验

比较检验

一、为什么要引入比较检验

我们要比较两个学习器的学习性能，不仅仅需要求出两个关于性能度量的值，然后定量比较就完事儿的。因为，机器学习中，学习器性能的比较涉及到很多方面，而这些方面有时候又有矛盾关系。

我们需要考虑的评估学习性能的因素主要有以下几点：

• 泛化能力，即机器学习算法对新样本的适应能力。举个例子，我们高考的时候多半都会刷“五三”，刷了很多题，但是在高考的时候有些同学可以考的很好，但是有些就考的不行。原因在于高考的题目不可能是我们平时训练的原题，没有人做过，而不同的同学由于泛化能力不一样，因此举一反三的能力也就有了差距，最后导致大家的成绩天差地别。把高中生这种举一反三的能力放到机器学习上，就是学习器的泛化能力了。
• 测试集的选择，不同大小，不同样例的测试集导致的训练结果可能是不一样的。
• 算法的随机性，因为机器学习是有黑盒性质的，我们无法得知里面的具体运行过程，有可能相同的测试集、在同一个学习器上以相同的参数来运行，会出现不一样的结果；

因此，我们需要专门研究一下机器学习的比较检验问题。

二、几种比较检验方法

1、假设检验——二项检验

首先引入两个概念：

• 第一个叫做泛化错误率$e$，是指学习器在一般情况下，对一个样本分类出错的概率，实际情况下我们是无法得知它的准确值的；
• 第二个叫做测试错误率$e^{\prime }$，即学习器在测试一个m大小的样本集时恰好有$e^{\prime }m$个样本被分错类了，我们一般情况下只能获得这个值；

两者区别就是：泛化错误率是一个理论上的值，无法获得，而测试错误率是一个我们可以测量得到的值。统计假设检验的方法就是用$e^{\prime }$估计$e$的值；

一个泛化错误率为$e^{\prime }$的学习器来测试一个大小为$m$的测试样例集，只可能有分对和分错两种情况，其中$e^{\prime }m$个分错，其余的分对，因此这就是一个典型的二项分布，那么我们可以得出测试的错误率分布函数：
$$P(e^{\prime };e)=\left(\begin{array}{c}m\\ e^{\prime }m\end{array}\right)e^{e^{\prime }m}(1-e{)}^{m-e^{\prime }m}$$
对$P(e^{\prime };e)$作关于$e$的一阶导，令$\delta P(e^{\prime };e)/\delta e=0$，解得$e=e^{\prime }$时，$P(e^{\prime };e)$最大；$|e-e^{\prime }|$增大，$P(e^{\prime };e)$减小，就像二项分布一样；

之后便是检验的过程，由于西瓜书上讲的有点晦涩，所以我尽量用稍微简单点的方式描述一下二项假设检验。

前提条件：对于一个分布函数，我们已知这是一个二项分布了，但是这个二项分布的参数（二项分布就只有一个参数，就是正例概率p，在这个例子里面是泛化错误率）的取值是未知的。

假设方法

• 我们可以用假设的办法，人为的规定一个参数取值的“阈值范围”，在这个例子中，我们假设$e\le e_0$；

• 然后我们根据客观需要或者一些计算公式（这里不再赘述，具体问题具体分析），再人为设定一个用于检验的置信度$\alpha$，这个变量表示出现明显错误的标准，比如这个二项分布中大于6的概率为$\alpha$，我设定阈值为$\alpha$就说明我认为如果学习器分类错误个数大于6，那么就属于明显错误，这个假设是不成立的；

• 反之，$1-\alpha$则表示不会出现明显错误的标准，也就是可信任的标准；

我们现在就是要利用这个$1-\alpha$，来推出在这个置信度下，我们假设的$e_0$是不是合理的；

判断假设的合理性

判断合理性一共有两种方法，我主要介绍一下西瓜书上的那种；

大致的思路就是：利用我们设定好的$1-\alpha$的值作为约束，求得分布曲线不大于这个值的积分面积。在书中的例子中用的是条形1统计图，那就把每一条的横纵坐标相乘再做一个求和运算，求出不大于$1-\alpha$的最大值，最后求得这个时候的$e_i$；

写成计算公式是这样的：
$$\sum _{i=e_{0}m+1}^m\left(\begin{array}{c}m\\ i\end{array}\right)e^i(1-e{)}^{m-i}<1-\alpha$$
意思就是对这个条形统计图从最左边的一条开始累加“横坐标和纵坐标的面积”，然后一直加到刚好不大于$1-\alpha$为止。

我们取出此时的$i$，对应的横坐标即为可接受的阈值标准，再拿我们预先设定好的$e_0$跟它作比较，若$e_0$在小于这个阈值标准，则说明该假设可接受，是合理的假设；否则就是不合理的，需要重新假设。

其实说到头，这就是一个“自编自导”的过程，总结起来就是首先通过二项分布的特征，得到一个大致的阈值，然后在这个阈值中寻找更为精确的点。针对不同的学习器，我们可以使用这种方法，来人为设定参数，比较两个学习器的好坏。

2、假设检验——t检验

很多时候我们为了确保结果的普适性和精确度，我们会做很多次估计检测，假设我们得到了k个错误率$e_1^{\prime },....,e_k^{\prime }$，那么我们很容易得到平均错误率$\mu$和方差${\delta }^2$为：
$$\begin{gathered} \mu =\frac{1}{k}\sum _{i=1}^k{e}_i^{\prime }， \\ {\delta }^2=\frac{1}{k-1}\sum _{i=1}^k(e_i^{\prime }-\mu {)}^2. \end{gathered}$$
由于每次估计检测都是独立的，所以这个概率分布函数可以写成：
$$T_t=\frac{\sqrt{k}(\mu -e_0)}{\delta }$$
其中这个$e_0$是泛化错误率，这是一个满足正态分布的函数；

接下来我们还是跟二项检验一样，设定一个置信度$\alpha$，在正态分布曲线两边的$\frac{\alpha }{2}$处各取一个明显错误区间，如图所示：

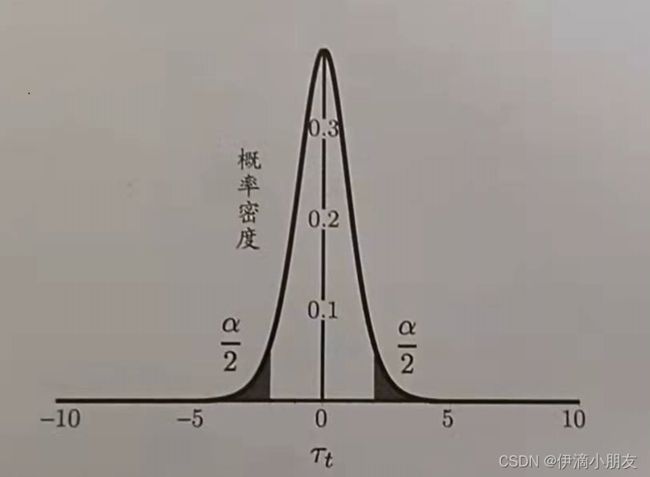
然后假设一个阈值区间$\mu =e^{\prime }$，计算白色图像曲线下的定积分（条形统计图计算方法参照二项检验），将两个假设做一个对比，如果$e^{\prime }$在置信度$\alpha$推出的区间内，则说明是可接受的。

双边t检验常用的临界值表：

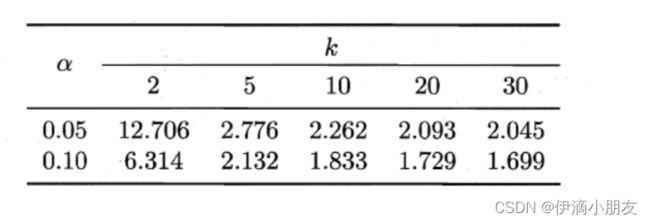
这一部分的总体过程跟二项检验很相似，除了公式和分布曲线不一样，其余的步骤都是可以仿照二项检验的步骤的，这里就不再赘述。

3、交叉验证t检验

以上两个方法主要针对单个学习器性能的衡量，如果对于多学习器来说，则可以用k折交叉验证t检验来完成。

比如两个学习器A和B经过k次测试的错误率分别为$e_1^A,...,e_k^A$，$e_1^B,...,e_k^B$，其中$e_i^A,e_i^B$是经过k折训练得到的第i折结果，对每一组训练测试结果求差值：${\Delta }_i=e_i^A-e_i^B$；

假设每次测试都是相互独立的，所以我们可以把${\Delta }_1...{\Delta }_k$视作k次性能差值的独立采样过程，计算出这组数据的均值$\mu$和方差${\delta }^2$，因此我们有：
$$\alpha isacceptables.t.T_t=abs(\frac{\sqrt{k}\mu }{\delta })<t_{\frac{\alpha }{2}}$$
这个过程的思路同样也是设定一个置信度$\alpha$，然后判断阈值是否在置信度可接受范围内。

实际上，我们的训练\测试集很容易产生重叠，所以每一次的测试不一定是相互独立的。

我们可以粗略的推测一下，如果我们的训练测试集出现重叠，那么我们得到的k折测试结果是有一定程度的相关性和相似度的，而我们如果还是假设这些测试结果相互独立，也就是说原本“粘合在一起的一堆结果”，我们把它们视作“没有粘合在一起”，那么就相当于我们假设的可接受范围实际上是偏大的，我们会高估假设成立的概率。

所以我们可以采用“5×2交叉验证”，来缓解这个问题。所谓5×2，就是做5次2折交叉验证，在每次2折交叉验证之前一定要把数据打乱，保证划分不重复。基本思路如下：

• 对于两个学习器A和B，每次2折交叉验证会产生两组测试错误率，我们对它们分别求差，得到第1折上的差值${\Delta }_i^1$和第2折上的差值 ${\Delta }_i^2$；

• 对第一次2折验证的两个结果取平均值${\mu }^{\prime }$，对每次2折实验结果做方差${\delta }^{\prime 2}$，平均值采用之前第一折的均值${\mu }^{\prime }$；

• 其概率分布函数为：
  $$T_t^{\prime }=\frac{{\mu }^{\prime }}{\sqrt{0.2{\sum }_{i=1}^5{\delta }_i^2}}$$

为什么这样就可以缓解测试结果之间的独立性问题了呢？其实很简单，因为我们的均值只是一次测试结果的一组错误率，此后所有的测试结果在计算方差的时候都用的是前面的一组错误率，因此方差的大小仅仅跟原始数据和第一次测试的错误率有关。但是我觉得这种方法得建立在第一次测试的结果比较贴合实际的基础上才会比较好的说服力（个人的一点想法，欢迎大佬指正）。

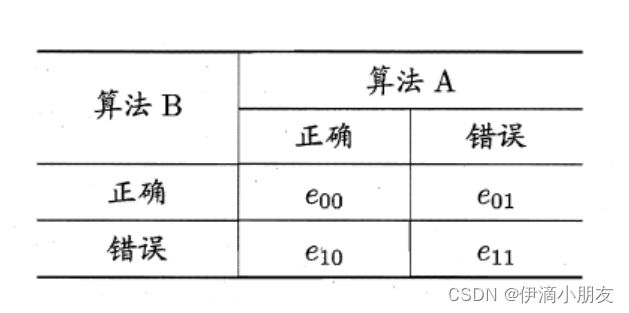
4、McNemar检验

这个检验方法的主要思路是针对两个二分类学习器的分类结果列出列联表，然后推出两个学习器性能差别的卡方分布函数，再作假设检验；接下来大致的描述一下这个方法的步骤：

• 首先对A、B两个学习器的二分类结果列出列联表：
  

• 然后取$|e_{01}-e_{10}|$，这个变量服从正态分布；这个检验方法考虑变量
  $$T_{x^2}=\frac{(|e_{01}-e_{10}|-1{)}^2}{e_{01}+e_{10}}$$

• 这是一个自由度为1的卡方分布，剩余的假设检验步骤同上：做出假设置信度、推出可接受的范围，检验假设阈值是否在可接受范围内、得出结论。

5、Friedman检验和Nemenyi后续检验

交叉验证t检验和McNemar检验只适用于两两比对，当要比对多个算法的学习器的时候，显然将算法两两比对太麻烦了，所以引入一种可以在同一组数据集上对多个算法进行比对的检验方法。

F检验法的基本思想是在同一组数据集上，根据测试结果对学习器的性能进行排序，赋予序值1,2,3…，相同则平分序值，如下图所示：

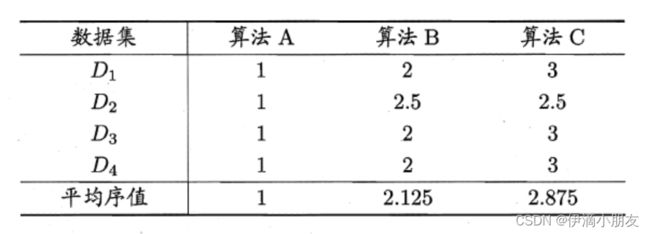
性能越好，赋予的值就越小，然后计算出每个算法在各个数据集上的平均序值$r_i$；

这里需要注意，表中的数据只是一个特例，有了这个平均序值并不能完全说明序值小的算法一定更好，因为针对不同的数据集，也许A算法会不如B算法，而且两种学习器在同一个数据集上也可能会有相似的结果，所以我们需要用一个估计阈值，来判定哪个算法更加好。

假设在N个数据集上比较k个算法，$r_i$的均值和方差分别是$(k+1)/2$和$(k^2-1)/12N$，得到分布函数（推导过程略）：
$$\begin{gathered} T_{X^2}=\frac{12N}{k(k+1)}(\sum _{i=1}^k{r}_i^2-\frac{k(k+1{)}^2}{4}) \\ {T}_F=\frac{(N-1)T_{X^2}}{N(k-1)-T_{X^2}} \end{gathered}$$
$T_{X^2}$为原始Friedman检验分布函数，$T_F$为F检验分布函数；这个算法中，西瓜书明确的给了一个临界值表：

是否可接受的检验仍然同上。

如果所有算法的性能相同这个假设被拒绝了，则需要进行后续检验，来对算法做一个进一步的比较。因为前面的步骤我们只是了解了这k个算法并不是全部性能相同，现在我们需要把性能不相同的学习器“找出来”，并且比较出孰优孰劣。

下面介绍一下Nemenyi检验算法的具体过程：

基本原理是根据两个算法的平均序值之差与CD值比较，如果均值差超过CD值，则说明这两个学习器的性能有差别。

CD值计算公式如下：
$$CD=q_{\alpha }\sqrt{\frac{k(k+1)}{6N}}$$
其中$q_{\alpha }$值的取值表如下：

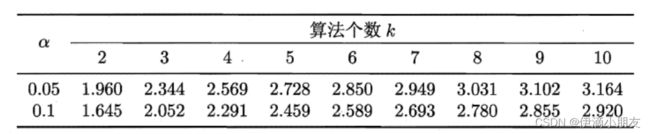
如果两个序值之差大于CD值，那么平均序值小的算法在一定程度上是要优于平均序值大的算法。

所以回过头来看，平均序值只是一个参考的方面，我们还需要在Friedman检验和Nemenyi后续检验的前提下，才可以比较严谨的用平均序值来衡量算法的优劣。

下一节：机器学习笔记3——线性回归