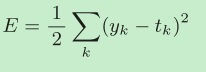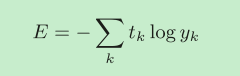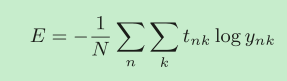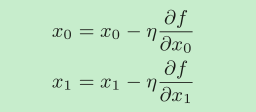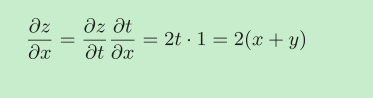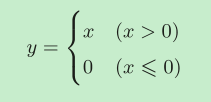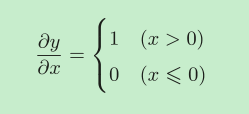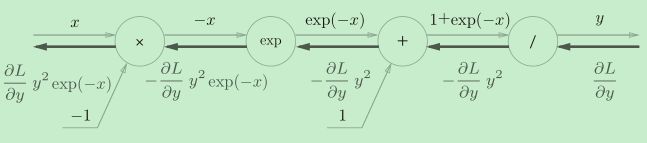Python深度学习入门笔记 2

Python深度学习入门笔记 2

1.神经网络的学习

内容

标题中的学习是指从训练数据中自动获取最优权重参数的过程。

为了使神经网络能进行学习，将导入损失函数这一指标，目的就是以该损失函数为基准，找出能使它的值达到最小的权重参数。为了找出尽可能小的损失函数的值，我们将介绍利用了函数斜率的梯度法。

从数据中学习

讲过上一部分的学习，我们已经知道多层感知机只要配置好合适的参数，就可以实现任何函数的功能。然而在实际的神经网络中，参数的数量成千上万，在层数更深的深度学习中，参数的数量甚至可以上亿，想要人工决定这些参数的值是不可能。这时，如果我们的神经网络可以“从数据中学习”，那岂不是可以大大地解放脑力。

所谓“从数据中学习”，是指可以由数据自动决定权重参数的值！！数据是机器学习的核心。

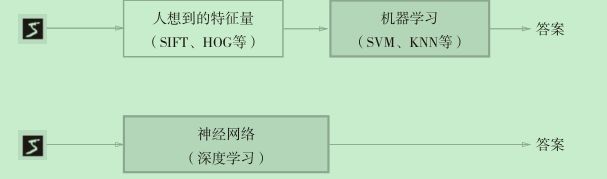
以图像识别为例，说明机器学习和深度学习之间的区别：

在机器学习中，虽然可以由机器从其收集到的数据中发现规律，但是图像转换成向量时使用的特征量仍然是认为设计的，比如识别人脸和识别花朵就需要不同的的特征量。

而在深度学习中，连图像中包含的重要特征量也都是由机器来学习调整的。

深 度 学 习 有 时 也 称 为 端 到 端 机 器 学 习（end-to-end machine
learning）。这里所说的端到端是指从一端到另一端的意思，也就是从原始数据（输入）中获得目标结果（输出）的意思。

训练数据和测试数据

机器学习中，一般将数据分为训练数据和测试数据两部分来进行学习和实验等。首先，使用训练数据进行学习，寻找最优的参数；然后，使用测试数据评价训练得到的模型的实际能力。

为什么需要将数据分为训练数据和测试数据呢？这是因为我们希望模型具有适应性或泛化能力，泛化能力是指模型在训练数据上达到很好地准确性之后，也能在其他的数据上表现出接近的准确性。获得泛化能力是机器学习的最终目标。

训练数据也可以称为监督数据。

如果没有测试数据，用整个数据集去学习和评价参数，是无法进行正确评价的，这样会导致可以顺利地处理某个数据集，但无法处理其他数据集的情况。这种只对某个数据集过度拟合的状态称为过拟合（over fitting）。

损失函数

神经网络的学习需要通过某个指标表示现在模型的状态，然后以这个指标为基准，寻找最优权重参数。在神经网络的学习中所用的指标称为损失函数（loss function）。这个损失函数可以使用任意函数，但一般用均方误差和交叉熵误差等。

损失函数是表示神经网络性能的“恶劣程度”的指标，即当前的神经网络对监督数据在多大程度上不拟合，在多大程度上不一致。

均方误差

y_k是表示神经网络的输出，t_k表示监督数据，k表示数据的维数。

交叉熵误差

y_k是神经网络的输出，t_k是正确解标签。并且，t_k中只有正确解标签的索引为1，其他均为0（one-hot表示）。

这里介绍一下一种数据表示方法：将正确解标签表示为1，其他标签表示为0的表示方法称为one-hot表示。

因为只有正确数据对应的t_k是1，其他的都是0，所以实际上只计算对应正确解标签的输出的自然对数。

mini-batch学习

计算损失函数时必须将所有的训练数据作为对象。也就是说，如果训练数据有100个的话，我们就要把这100个损失函数的总和作为学习的指标。如果要求所有训练数据的损失函数的总和，以交叉熵误差为例，可以写成下面的式子

实际上就是损失函数的平均值。

然而，如果数据集的训练数据很多，以全部数据为对象求损失函数的和，则计算过程需要花费较长的时间。如果遇到大数据，数据量会有几百万、几千万之多，这种情况下以全部数据为对象计算损失函数是不现实的。因此，我们从全部数据中选出一部分，作为全部数据的“近似”。神经网络的学习也是从训练数据中选出一批数据（称为mini-batch,小批量），然后对每个mini-batch进行学习，这种学习方式称为mini-batch学习。

为何要设定损失函数

在神经网络的学习中，寻找最优参数（权重和偏置）时，要寻找使损失函数的值尽可能小的参数。为了找到使损失函数的值尽可能小的地方，需要计算参数的导数（确切地讲是梯度），然后以这个导数为指引，逐步更新参数的值。

假设有一个神经网络，现在我们来关注这个神经网络中的某一个权重参数。对该权重参数的损失函数求导，如果导数的值为负，通过使该权重参数向正方向改变，可以减小损失函数的值；反过来，如果导数的值为正，则通过使该权重参数向负方向改变，可以减小损失函数的值。

那为什么不用准确性这个简单的方法来作为调整参数的指标呢？因为如果以识别精度为指标，则参数的导数在绝大多数地方都会变为0，这时就没有办法通过导数来调整参数的值。

假设我们是对手写的一个数字进行识别，那么准确性就是 识别准确的个数/总个数

而这个值，是不连续的，离散的。

识别精度对微小的参数变化基本上没有什么反应，即便有反应，它的值也是不连续地、突然地变化，因此我们不能使用准确性来作为调整参数的指标。

求导

数值微分

数值微分是一种用数值方法近似求解函数的导数的过程，我们可以计算函数f在(x + h)和(x − h)之间的差分，用这个差分来近似x点的切线（导数值），这种方法也叫中心差分，（而(x + h)和x之间的差分称为前向差分）。

偏导数

有多个变量的函数的导数称为偏导数，计算偏导数需要将其他变量固定为某个值，并对其中一个变量求导。

梯度

像这样的由全部变量的偏导数汇总而成的向量称为梯度（gradient）。

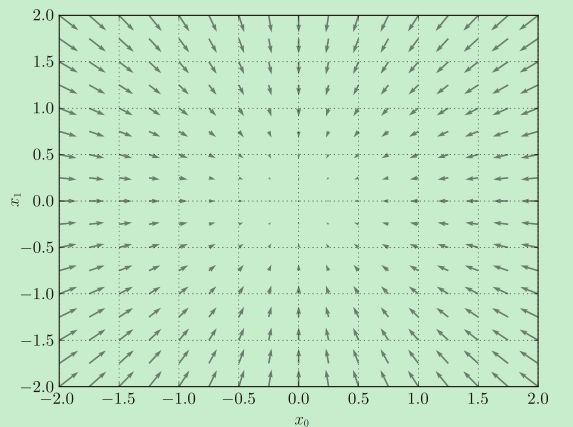
梯度呈现为有向向量（箭头）。观察图，我们发现梯度指向函数f(x0,x1)的“最低处”（最小值），就像指南针一样，所有的箭头都指向同一点。其次，我们发现离“最低处”越远，箭头越大。

严格地讲，梯度指示的方向是各点处的函数值减小最多的方向。

梯度法

神经网络必须在学习时找到最优参数（权重和偏置）。这里所说的最优参数是指损失函数取最小值时的参数。一般而言，损失函数很复杂，参数空间庞大，我们不知道它在何处能取得最小值。而通过巧妙地使用梯度来寻找函数最小值（或者尽可能小的值）的方法就是梯度法。

梯度表示的是各点处的函数值减小最多的方向。因此，无法保证梯度所指的方向就是函数的最小值或者真正应该前进的方向。实际上，在复杂的函数中，梯度指示的方向基本上都不是函数值最小处。

虽然梯度法是要寻找梯度为0的地方，但是那个地方不一定就是最小值（也有可能是极小值或者鞍点（从某个方向上看是极大值，从另一个方向上看则是极小值的点）。此外，当函数很复杂且呈扁平状时，学习可能会进入一个（几乎）平坦的地区，陷入被称为“学习高原”的无法前进的停滞期。

虽然梯度的方向并不一定指向最小值，但沿着它的方向能够最大限度地减小函数的值。因此，在寻找函数的最小值（或者尽可能小的值）的位置的任务中，要以梯度的信息为线索，决定前进的方向。此时梯度法就派上用场了。在梯度法中，函数的取值从当前位置沿着梯度方向前进一定距离，然后在新的地方重新求梯度，再沿着新梯度方向前进，如此反复，不断地沿梯度方向前进。

用数学式子来表示梯度法：

η表示更新量，在神经网络的学习中，称为学习率（learning rate）。学习率决定在一次学习中，应该学习多少，以及在多大程度上更新参数。

上面的式子是一次更新的式子，实际上这个式子会反复执行很多次。

学习率需要事先确定为某个值，比如0.01或0.001。一般而言，这个值过大或过小，都无法抵达一个“好的位置”。在神经网络的学习中，一般会一边改变学习率的值，一边确认学习是否正确进行了。

学习率过大的话，会发散成一个很大的值；反过来，学习率过小的话，基本上没怎么更新就结束了。也就是说，设定合适的学习率是一个很重要的问题。那么学习率可以像参数一样用让机器来自己学习然后调整吗？很遗憾，不能。

像学习率这样的参数称为超参数。这是一种和神经网络的参数（权重和偏置）性质不同的参数。学习率这样的超参数则是人工设定的。一般来说，超参数需要尝试多个值，以便找到一种可以使学习顺利进行的设定。

学习算法的实现

1. 从训练数据中随机选出一部分数据，这部分数据称为mini-batch。
2. 计算梯度。求出各个权重参数的梯度。
3. 更新参数。将权重参数沿梯度方向进行微小更新。
4. 重复步骤1、步骤2、步骤3。

2.误差反向传播法

上面说的方法看起来已经非常不错了，但是数值微分计算导数虽然简单，也容易实现，但是计算上比较费时间。因此我们学习一个高效的计算权重参数的梯度的方法——误差反向传播法。

基于计算图理解理解误差反向传播

计算图将计算过程用图形表示出来。这里说的图形是数据结构图，通过多个节点和边表示（连接节点的直线称为“边”）。

计算图通过节点和箭头表示计算过程。节点用○表示，○中是计算的内容。将计算的中间结果写在箭头的上方，表示各个节点的计算结果从左向右传递。

上面的图中，“从左向右进行计算”是一种正方向上的传播，简称为正向传播（forward propagation）。同样“从右向左进行计算”是一种反方向上的传播，简称为反向传播（backward propagation）。反向传播将在接下来的导数计算中发挥重要作用。

计算图的特征是可以通过传递“局部计算”获得最终结果。

各个节点处只需进行与自己有关的计算（在这个例子中是对输入的两个数字进行加法
运算），不用考虑全局。

计算图将复杂的计算分割成简单的局部计算，和流水线作业一样，将局部计算的结果传递给下一个节点。

计算图的优点：局部计算，将中间的计算结果全部保存起来。实际上，使用计算图最大的原因是，可以通过反向传播高效计算导数。

通过反向传播高效计算导数

如图所示，反向传播传递“局部导数”，将导数的值写在箭头的下方，反向传
播从右向左传递导数的值（1 → 1.1 → 2.2）。从这个结果中可知，“支付金额
关于苹果的价格的导数”的值是2.2。而且计算中途求得的导数的结果（中间传递的导数）可以被共享，从而可以高效地计算多个导数。

假设存在y = f(x)的计算，这个计算的反向传播如图所示。

反向传播的计算顺序是，将信号E乘以节点的局部导数（dy/dx），然后将结果传递给下一个节点。这里所说的局部导数是指正向传播中y = f(x)的导数，也就是y关于x的导数（dy/dx）。

链式法则

链式法则是关于复合函数的导数的性质，如果某个函数由复合函数表示，则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示。

反向传播是基于链式法则的。

反向传播

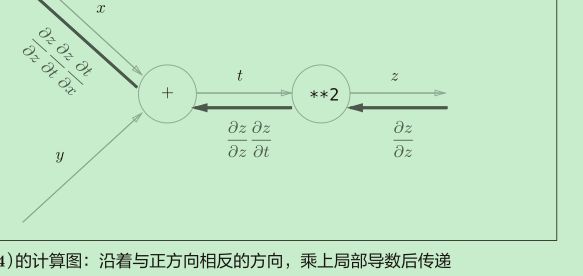
加法节点的反向传播

加法节点的反向传播只乘以1，所以输入的值会原封不动地流向下一个节点。

乘法节点的反向传播

乘法的反向传播会将上游的值乘以正向传播时的输入信号的“翻转值”后传递给下游。

举个例子

简单层的实现

我们把要实现的计算图的乘法节点称为“乘法层”（MulLayer），加法节点称为“加法层”（AddLayer）。

这里所说的“层”是神经网络中功能的单位。比如，负责 sigmoid 函数的
Sigmoid、负责矩阵乘积的Affine等，都以层为单位进行实现。

乘法层的实现

层的实现中有两个共通的方法（接口）forward()和backward()。forward()
对应正向传播，backward()对应反向传播。

class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None
    def forward(self, x, y):
        self.x = x
        self.y = y
        out = x * y
        return out
    def backward(self, dout):
        dx = dout * self.y # 翻转x和y
        dy = dout * self.x
        return dx, dy

forward()接收x和y两个参数，将它们相乘后输出。

backward()将从上游传来的导数（dout）乘以正向传播的翻转值，然后传给下游。

使用方法

apple = 100
apple_num = 2
tax = 1.1
# layer
mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()
# forward
apple_price = mul_apple_layer.forward(apple, apple_num)
price = mul_tax_layer.forward(apple_price, tax)
print(price) # 220

注意，调用backward()的顺序与调用forward()的顺序相反。此外，要注
意backward()的参数中需要输入“关于正向传播时的输出变量的导数”。

加法层的实现

class AddLayer:
    def __init__(self):
        pass
    def forward(self, x, y):
        out = x + y
        return out
    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1
        return dx, dy

激活函数层的实现

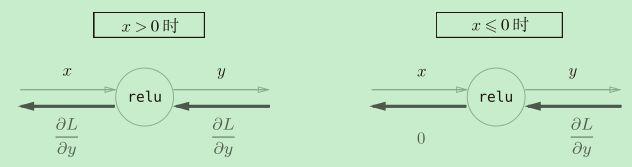
ReLU层

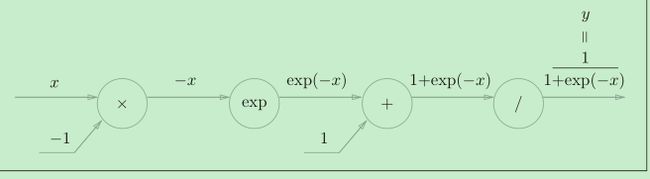
Sigmoid层

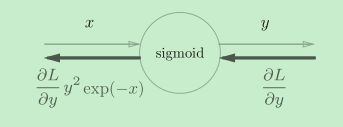
对于y=1/x，反向传播时，会将上游的值乘以−y2（正向传播的输出的平方乘以−1后的值）后，再传给下游。

而对于y = exp(x)，上游的值乘以正向传播时的输出（这个例子中是exp(−x)）后，再传给下游。

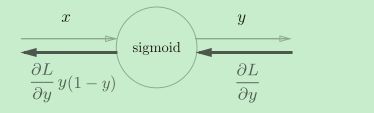
省略中间内容后简化为

Affine/Softmax层的实现

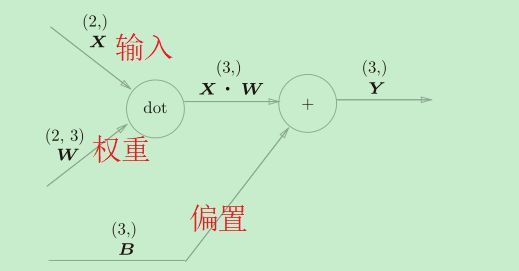
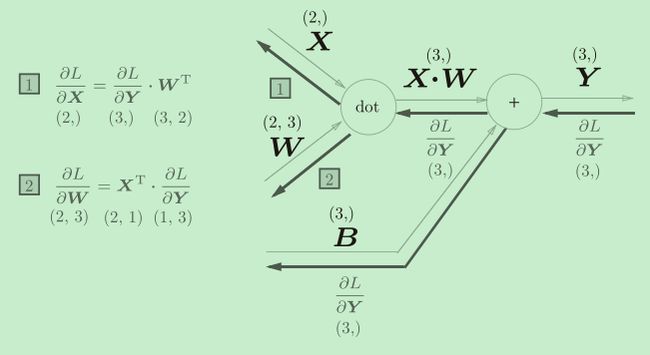
Affine层

在几何中，仿射变换包括一次线性变换和一次平移，分别对应神经网络的加权和运算与加偏置运算。所谓Affine层其实就是神经网络中两层之间的计算

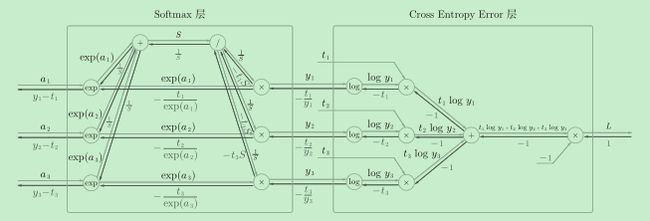
Softmax-with-Loss 层

神经网络输出层的Softmax函数在加上作为损失函数的交叉熵误差（cross entropy error）合在一起称为Softmax-with-Loss 层。

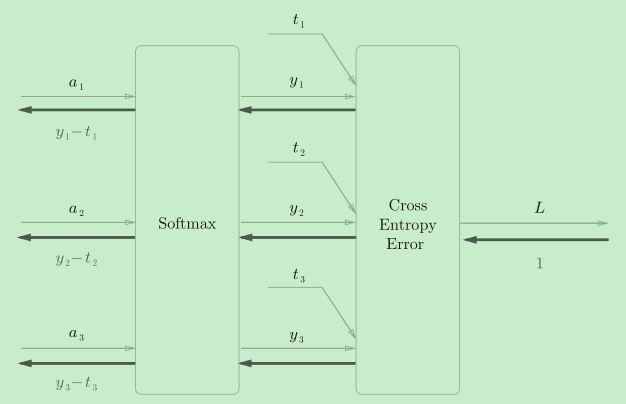
简化

Softmax层的反向传播得到了（y1−t1, y2−t2, y3−t3）这样“漂亮”的结果。

由于（y1, y2, y3）是Softmax层的输出，（t1, t2, t3）是监督数据，所以（y1−t1, y2−t2, y3−t3）是Softmax层的输出和标签数据的差分。

神经网络的反向传播会把这个差分表示的误差传递给前面的层，这是神经网络学习中的重要性质。神经网络学习的目的就是通过调整权重参数，使神经网络的输出（Softmax的输出）接近标签数据。

实际上，这样“漂亮”的结果并不是偶然的，而是为了得到这样的结果，特意设计了交叉熵误差函数。同样地，回归问题中输出层使用“恒等函数”，损失函数使用“平方和误差”，也是出于同样的理由。

神经网络学习的全貌图

将之前代码中计算梯度的部分换成误差反向传播的方法，然后用层来构建神经网络的运算，这就是神经网络的实现了。

# coding: utf-8
import sys, os

sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict


class MyTwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        # 初始化权重
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

        # 生成层
        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
        self.lastLayer = SoftmaxWithLoss()

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)

        return x

    # x:输入数据, t:监督数据
    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t)

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1: t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    # x:输入数据, t:监督数据
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)

        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])

        return grads

    def gradient(self, x, t):
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        dout = self.lastLayer.backward(dout)

        # 获取一个副本
        layers = list(self.layers.values())
        # 翻转
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 设定
        grads = {}
        grads['W1'] = self.layers['Affine1'].dW
        grads['b1'] = self.layers['Affine1'].db
        grads['W2'] = self.layers['Affine2'].dW
        grads['b2'] = self.layers['Affine2'].db

        return grads