## 基于R语言的信用评分卡模型
信用评分卡模型是最常见的金融风控手段之一,它是指根据客户的各种属性和行为数据,利用一定的信用评分模型,对客户进行信用评分,据此决定是否给予授信以及授信的额度和利率,从而识别和减少在金融交易中存在的交易风险。通过将模型变量WOE编码的方式离散化之后用LOGISTIC模型进行二分类的广义线性模型。
本文通过对kaggle上的Give Me Some Credit数据的挖掘分析,结合信用评分卡的建立原理,从数据的预处理、变量筛选、建模分析、模型评估、创建信用评分卡到建立自动评分系统,创建了一个简单的信用评分系统。
1.工作原理
客户的信用评分卡是基于统计模型,它通过对当前申请人的各项资料进行评估并给出一个分数,该评分能定量的对申请人的偿债能力做出预判。
评分卡由一系列的特征项组成,比如申请人的年龄、月收入、信贷数量等;每个特征项都有一系列的可能的属性,例如每个年龄段是年龄特征项的属性。在开发评分卡系统模型中,先确定属性与申请人未来信用表现之间的相互关系,然后给属性分配适当的分数权重,分配的分数权重要反映这种相互关系。分数权重越大,说明该属性表示的信用表现越好。一个申请的得分是其属性分值的简单求和。如果申请人的信用评分大于等于金融放款机构所设定的界限分数,此申请处于可接受的风险水平并将被批准;低于界限分数的申请人将被拒绝或给予标示以便进一步审查。
2.开发流程
数据获取 → 数据前期探索 → 数据预处理 → 变量筛选 → 逻辑回归模型开发 → 模型评估 → 生成评分卡
2.1 数据导入
cs<-read.csv("cs-training.csv")
cs<-cs[,-1]
names(cs)<-c("好坏客户","可用额度比值","年龄","逾期30至59天比数","负债率","月收入","信贷数量","逾期90天比数", "固定资产贷款量","逾期60至89天比数","家属数量")
**2.2 数据预处理
2.2.1 缺失值处理**
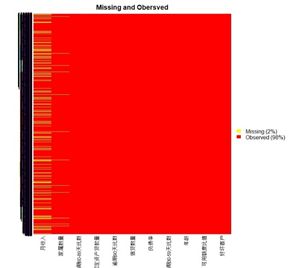
missmap(cs,main="Missing and Obersved",col=c("yellow","red"))
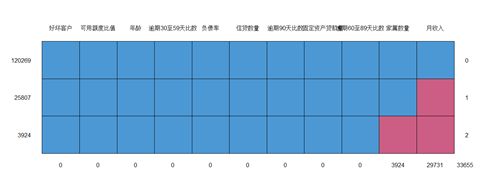
md.pattern(cs)
对缺失值进行可视化展示,发现家属数量数据缺失3924,占比2.6%,删除对应数据行;月收入行缺失数据29731,占比较大,可以中位数进行填充。
cs<-cs[!is.na(cs$家属数量),]
cs$月收入<-na.roughfix(cs$月收入)
2.2.2 异常值处理
boxplot(cs[,c(2,5)])
boxplot(cs[,3],maxin="BOXPLOT",xlab="年龄")
boxplot(cs[,c(4,8,10)])
boxplot(cs[,c(7,9)])
异常值处理消除不合逻辑的数据和超级离群的数据,可用额度比值应该小于1,年龄为0的是异常值;通过箱线图可以发现,逾期天数笔数大于80的是超级离群数据,固定资产贷款量大于50的是超级离群数据,将这些离群值过滤掉,筛选出剩余部分数据。
cs<-cs[-which(cs$可用额度比值>1),]
cs<-cs[-which(cs$年龄==0|cs$年龄>70),]
cs<-cs[-which(cs$逾期30至59天比数>80),]
2.2.3 变量相关性分析
即使不进行线性相关性分析也不会影响模型的整体性能,进行相关性分析只是为了让我们的模型更易于解释,保证不同的分箱的得分正确。相关系数如下,表征两参数间的的线性相关程度,绝对值越大表明相关程度越大。
cor_all<-cor(cs[,1:11])
corrplot(cor_all,method="number")

从图中可知,参数间的相关性均小于0.6,同时亦可可以初步判断不存在多重共线性问题。当然我们在建模后还可以用VIF(方差膨胀因子)来检验多重共线性问题。如果存在多重共线性,即有可能存在两个变量高度相关,需要降维或剔除处理。
2.2.4 变量筛选
本文通过随机森林模型对变量的重要性排序,将重要性较低的变量剔除。随机森林模型是决策树模型的组合方法,通过有放回抽样的方法,从样本集中选择k个样本作为训练集,构成k和决策树模型;每一个树的每个节点随机的抽取metry个特征计算信息增益,选择分裂方向。将生成的多棵树组成随机森林,用随机森林对样本进行分类,分类结果按树分类器投票多少而定。变量重要性(VIM,Gini)是通过计算变量在所有树的每个节点分裂不纯度的平均该变量,该值越大,表示该值带来的信息增益越大,便越重要;另一个以OBB错误率差值表征变量重要性,首先计算单棵树的OBB错误率,随机替换一个变量,重新计算OBB错误率,两次错误率的差值越大,表明被替换的标量越重要,此处用OBB错误率差值表征。
set.seed(123)
crf<-cforest(好坏客户~.,control=cforest_unbiased(mtry=3,ntree=50),data=cs)
varim<-data.frame(varimp(crf))
var<-data.frame(colnames(cs)[2:11],varim$varimp.crf.)
var<-var[order(-var$varim.varimp.crf.),]

如上为重要性排名,可以看出信贷数量家属数量相较于逾期90天比数逾期30天~59天比数,重要程度低很多。此处先不对变量进行删减,可配合后续模型回归系数正负关系进行删减。
2.2.5 数据划分
我们利用caret包中的createDataPartition(数据分割功能)函数将数据随机分成相同的两份,其中。其中用于训练的数据占75%,用于检验模型的数据占比25%。
set.seed(123)
split<-createDataPartition(cs$好坏客户,p=0.75,list=FALSE,time=1)
train<-cs[split,]
test<-cs[-split,]
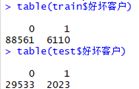
table(train$好坏客户)
table(test$好坏客户)
2.3.1 建模**
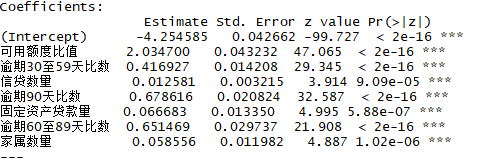
fit<-glm(好坏客户~.,binomial,train)
summary(fit)

各参数p-value均小于0.05,拒绝原假设,即所有变量均y值均显著。但是,可以注意到,年龄/负债率/月收入的系数为负,而对于分箱的WOE编码,分箱中坏客户占比越大,WOE值越大; 也就是说该分箱中客户为坏客户的概率就越大,对应的WOE值越大,即WOE与逻辑回归的预测结果 (坏客户的概率) 成正比,即各系数在评分卡模型中均应为正。
此处,首先根据2.2.3节中的变量重要性,选取重要程度最大的4个变量,即逾期90天比数/可用额度比值/逾期30至59天比数/逾期60至89天比数,按优先级从高到低逐渐添加变量,当新添加的变量之后,出现系数为负的情况,舍弃该变量,直到添加最后一个变量。最后结果为,删除年龄/负债率/月收入这3个变量。
cs2<-cs[,c(-3,-5,-6)]
set.seed(321)
split2<-createDataPartition(cs2$好坏客户,p=0.75,list=FALSE,time=1)
train2<-cs2[split2,]
test2<-cs2[-split2,]
table(train2$好坏客户)
table(test2$好坏客户)
fit2<-glm(好坏客户~.,binomial,train2)
summary(fit2)
下面首先利用模型对test数据进行预测,生成概率预测值。在R中,可以利用pROC包,它能方便比较两个分类器,还能自动标注出最优的临界点,图看起来也比较漂亮。在下图中最优点TNR=1-FPR=0.714,TPR=0.780,AUC值为0.826,说明该模型的预测效果还是不错的,正确率较高。
pre2<-predict(fit2,test2,type="response")
myRoc2<-roc(test2$好坏客户,pre2)
plot(myRoc2, print.auc=TRUE, auc.polygon=TRUE, grid=c(0.1, 0.2),
grid.col=c("green", "red"), max.auc.polygon=TRUE,
auc.polygon.col="skyblue", print.thres=TRUE)
将模型预测kaggle中的cs-test数据,经验证,模型预测accuracy为84.123%,说明模型可靠。
names(train2)<-colnames(cs3)
fit3<-glm(SeriousDlqin2yrs~.,binomial,train2)
summary(fit3)
Probability<-round(predict(fit3,cs_test,type="response"),3)
Probability<-as.data.frame(Probability)
cs_test$SeriousDlqin2yrs<-as.data.frame(Probability)
#cs_test$SeriousDlqin2yrs<-ifelse(cs_test$SeriousDlqin2yrs>=0.5,1,0)
ID<-as.data.frame(1:101503)
submit<-c(ID,Probability)
submit<-as.data.frame(submit)
names(submit)<-c("ID","Probability")