轻量级深度学习网络——ESPNet v2
- ESPNet v2
-
- 1 背景介绍
- 2 相关工作
-
- 2.1 轻量化的CNN架构
- 3 ESPNetv2
-
- 3.1 传统方法:2D卷积(看似3D实际是2D因为只在平面移动)
- 3.2 MoblieNet 深度可分离卷积(先将每个图片的深度计算出来,最后再进行组合)
- 3.3 ShuffleNet 分组卷积 (群卷积)
- 3.4 空洞卷积 Dilated Convolutions
- 3.5 ESPNetv1
- 3.6 EESP Unit
- 3.7 Strided EESP与图像输入快速连接
- 3.8 ESPNetv2的网络结构
- 4. 实验
-
- 4.1 图像分类
- 4.2 语义分割
-
- 4.3 目标检测
- 4.4 语言建模
- 5 消融实验
-
- 5.1 Convolution
- 5.2 HFF
- 5.3 Shortcut connection
- 5.4 Cyclic learning
- 6 总结
- 7 代码
ESPNet v2
在之前我们分享过两种轻量级网络MobileNet & MobileNet v2和ShuffleNet & ShuffleNet v2 而这次分享的ESPNetv2在轻量化上更上一层楼,这篇文章来自CVPR2019,按照作者的说法轻轻松松吊打上面的两种轻量级网络,那么就让我们来看一下吧!
论文地址:https://arxiv.org/pdf/1811.11431.pdf
开源代码:https://github.com/sacmehta/espnetv2
作者 Sachin Mehta, Mohammad Rastegari, Linda Shapiro, and Hannaneh Hajishirzi
这四个人分别来自华盛顿大学,微软的艾伦人工智能研究所和XNOR.ai公司;
2018年,这四个人和Anat Caspi一同发布了ESPNet,发表在了ECCV2018上。该网络的主要优点是在参数比目前的主流轻量级网络(如MobileNet, ShuffleNet)小很多的情况下,性能上却相差无几。
2019年,他们又发布了ESPNet的升级版——ESPNetv2,并在CVPR上发表。该网络在ESPNet的基础上继续被优化,参数相比前一代少了约四倍,而性能却只下降了很少的一点,这使得 ESPNetv2在轻型网络中占有一席之地。
1 背景介绍
作者介绍了一种轻量、效率高、通用的卷积神经网络ESPNetv2,用于对可视化数据和顺序数据进行建模。相比前一代网络,v2使用逐点群卷积和深度空洞可分离卷积。作者在四个不同的任务上使用该网络进行测试包括对象分类,语义分割,对象检测和语言建模,以此来证明ESPNetv2优于最目前比较先进的轻量级神经网络,而事实也恰好是这样。从结果来看,该网络在这四个任务上的表现均优于大部分轻量级神经网络(包括YOLOv2和ESPNet等)。
随着GPU的高速发展,卷积神经网络被越来越多地应用在了具有图像识别功能的工具中,如无人驾驶和机器人。然而,性能越好的神经网络往往需要更多的资源,这对于商业用途非常不利,我们试图寻找不需要那么多资源,还能够达到我们性能要求的神经网络,轻量级神经网络的研究因此发展。
目前主要有三种减少网络参数的方法:基于网络压缩的方法,基于低位表示的方法,分解卷积操作。本文介绍的ESPNetv2正是使用第三种方法来减轻网络的。
2 相关工作
2.1 轻量化的CNN架构
深度可分离卷积结构:
(1)deep-wise卷积:进行轻量级过滤,一个卷积核负责一个通道,一个通道只被一个卷积核卷积;
(2)point-wise卷积:通过学习输入通道的线性组合来沿着通道扩展特征图,卷积核的尺寸为 1×1×M,M为上一层deep-wise卷积的通道数。所以这里的卷积运算会将上一步deep-wise卷积的map在深度方向上进行加权组合,生成新的Feature map。有几个卷积核就有几个输出Feature map。
分组卷积: 将输入通道与卷积核分组,每组单独卷积;
假设上一层的输出feature map有N个,即通道数channel=N,也就是说上一层有N个卷积核。再假设群卷积的群数目M。那么该群卷积层的操作就是,先将channel分成M份。每一个group对应N/M个channel,与之独立连接。然后各个group卷积完成后将输出叠在一起(concatenate),作为这一层的输出channel。
空洞深度可分离卷积: 深度可分离卷积+空洞卷积;
空洞卷积:为了能够在不增加参数数量的情况下提高卷积核的感受野;在标准卷积核中的每个参数中间插入一定数量的0元素便得到了空洞膨胀的卷积核;膨胀率(即相邻元素之间的插0个数)为r。
channel shuffle: ShuffleNet的核心
channel split: 通道分割
神经网络架构搜索: 预定义一个词典,其中包含不同参数,例如:卷积层数、卷积单位、过滤器尺寸等;使用这个词典在网络空间中进行搜索;基于搜索的方法已经改进了MobileNetv2;
网络压缩: 主要通过散列、修剪、矢量量化和收缩等方法,以减小预训练的模型大小;这里主要强调的是对网络结构和通道的剪枝:CNN有相当数量的冗余权重,由于参数的稀疏性,在保证CNN精度的前提下,保留重要的权重(一般权重值越接近于0越不重要),去掉不重要的权重,简化网络模型复杂度。在CPU上无法实施,原因是数据查找和数据迁移操作占用较多资源。
低位网络: 通过量化模型的权重来减小模型大小和复杂度。使用较低位表示预训练模型中的权重,来代替32位高精度的浮点数;在简介中提及,减小后的模型通过使用逻辑门可以在CPU上实现快速计算。
3 ESPNetv2
在介绍ESPNET之前,我们需要对ESP所应用的各种卷积策略以及以及其参数量和感受野进行介绍和比对。
在这里感谢一下这两个博客的分享 (๑•̀ㅂ•́)و✧
https://blog.csdn.net/gwplovekimi/article/details/89890510
https://blog.csdn.net/sinat_37532065/article/details/85723068
3.1 传统方法:2D卷积(看似3D实际是2D因为只在平面移动)
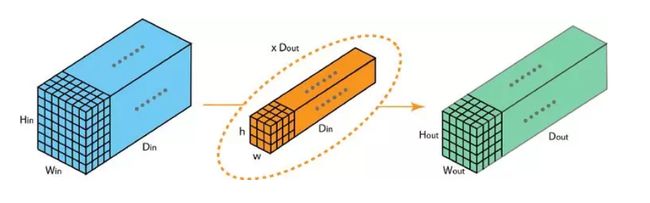
参数数量 h ∗ w ∗ D i n ∗ D o u t h*w*D_{in}*D_{out} h∗w∗Din∗Dout
现在我们需要对传统的网络结构进行优化,保证不改变输出大小的同时,降低网络中的参数量,从而达到轻量化的目的。而ESPNET则是基于MoblieNet以及ShuffleNet提出的深度分离式卷积和分组卷积实现轻量化的目的的。
3.2 MoblieNet 深度可分离卷积(先将每个图片的深度计算出来,最后再进行组合)
深度可分离卷积将整个过程划分为两步,第一步分别对每一层通道应用一个单独的卷积核,并将所有通道的输出作为第二步的输入。第二步根据输入图像的深度应用所需数量的1*1*输入图像深度的卷积核进行卷积,从而得到目标输出。
如图所示,我们来举一个具体的例子:
- 第一步:在 2D 卷积中分别使用 3 个卷积核(每个过滤器的大小为 3 x 3 x 1),而不使用大小为 3 x 3 x 3 的单个过滤器。每个卷积核仅对输入层的 1 个通道做卷积,这样的卷积每次都得出大小为 5 x 5 x 1 的映射,之后再将这些映射堆叠在一起创建一个 5 x 5 x 3 的图像,最终得出一个大小为 5 x 5 x 3 的输出图像。
- 第二步是扩大深度,我们用大小为 1x1x3 的卷积核做 1x1 卷积。每个 1x1x3 卷积核对 5 x 5 x 3 输入图像做卷积后都得出一个大小为 5 x 5 x1 的映射。这样的话,做 128 次 1x1 卷积后,就可以得出一个大小为 5 x 5 x 128 的层。深度可分离卷积完成这两步后,同样可以将一个 7 x 7 x 3 的输入层转换为 5 x 5 x 128 的输出层。
参数数量 h ∗ w ∗ 1 ∗ D i n + 1 ∗ 1 ∗ D i n ∗ D o u t h*w*1*D_{in}+1*1*D_{in}*D_{out} h∗w∗1∗Din+1∗1∗Din∗Dout
3.3 ShuffleNet 分组卷积 (群卷积)
参数数量 h ∗ w ∗ D i n k ∗ D o u t k ∗ k h*w*\frac{D_{in}}{k}*\frac{D_{out}}{k}*k h∗w∗kDin∗kDout∗k
上图表示的是被拆分为 2 个过滤器组的分组卷积。在每个过滤器组中,其深度仅为名义上的 2D 卷积的一半( D i n D_{in} Din / 2),而每个过滤器组都包含 D o u t D_{out} Dout /2 个过滤器。第一个过滤器组(红色)对输入层的前半部分做卷积([ : , : , 0 : D i n D_{in} Din/2]),第二个过滤器组(蓝色)对输入层的后半部分做卷积([ : , : , D i n D_{in} Din/2 : D i n D_{in} Din])。最终,每个过滤器组都输出了 D o u t D_{out} Dout/2 个通道。整体上,两个组输出的通道数为 2 x D o u t D_{out} Dout/2 = D o u t D_{out} Dout。之后,我们再将这些通道堆叠到输出层中,输出层就有了 D o u t D_{out} Dout 个通道。
3.4 空洞卷积 Dilated Convolutions
为了提高感受野,本网络采用了空洞卷积。
为了能够在不增加参数数量的情况下提高卷积核的感受野,便诞生了空洞卷积;
简单而言,在标准卷积核中的每个参数中间插入一定数量的0元素便得到了卷积膨胀的卷积核;
这样一来,对于一个N*N的卷积核,设膨胀率(即相邻元素之间的插0个数)为R,则其感受野增大到 [ ( N − 1 ) R + 1 ] 2 [(N-1)R+1]^2 [(N−1)R+1]2;
3.5 ESPNetv1
下面我们来介绍一下ESPNetv1
HFF (hierarchical feature fusion)
为了解决由于引入空洞卷积带来的网格效应(gridding artifact),将不同划分的特征图求和,之后再进行组合的过程。
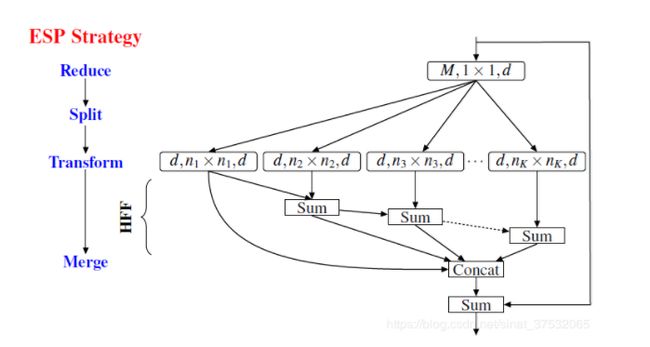
类比一个( w ∗ h ∗ M ∗ N w*h*M*N w∗h∗M∗N)大小的标准卷积核,即设输入的feature map大小为 128 ∗ 128 ∗ M 128*128*M 128∗128∗M,输出的feature map大小为 128 ∗ 128 ∗ N 128*128*N 128∗128∗N。ESP模块的具体计算如下:
① 经过Reduce以后,变为 128 ∗ 128 ∗ d 128*128*d 128∗128∗d
② 经过Split后,可以得到K张 128 ∗ 128 ∗ d 128*128*d 128∗128∗d的feature map;
③ 经过HFF融合以后,变为 128 ∗ 128 ∗ ( d ∗ K ) 128*128*(d*K) 128∗128∗(d∗K),注意d=N/K,所以输出大小为 128 ∗ 128 ∗ N 128*128*N 128∗128∗N;
如:当 n=3, N=M=128, K=4 时,一个标准卷积核参数量是一个ESP模块参数量的3.6倍,但ESP模块的感受野可以达到 17 ∗ 17 17*17 17∗17 。
这里还没有应用深度可分离卷积,而是只采用了空洞卷积,到达了提高卷积核感受野的作用。同时本网络也没用应用分组卷积,所以相比较于MobileNet 和 ShuffleNet,ESPNet的优势就在于其感受野,但参数量方面的确不占优势,这也就是ESPNETv2的主要研究方向。
3.6 EESP Unit
与ESP Unit相比,首先使用逐点群卷积(group point-wise convolution)替代了逐点卷积(point-wise convolutions)。然后使用深度空洞可分离卷积(depth-wise dilated separable convolutions)替代了 3 ∗ 3 3*3 3∗3空洞卷积(dilated convolutions)。这样的改动减少了卷积核的参数量。ESP Unit与EESP Unit参数量之比为:
M d + n 2 d 2 K M d g + ( n 2 + d ) d K \frac{Md+n^2d^2K}{\frac{Md}{g}+(n^2+d)dK} gMd+(n2+d)dKMd+n2d2K
当 M = 240 M=240 M=240, g = K = 4 g=K=4 g=K=4, d = M K = 60 d=\frac{M}{K}=60 d=KM=60,EESP Unit的参数量是ESP Unit的1/7。
在深度空洞可分离卷积与逐点群卷积中间添加HFF,去除了空洞卷积带来的栅格重影。
图1c与图1b中的主要区别就是,用k组的group point-wise convolution代替了单独计算k点的point-wise convolutions。从复杂度方面来看,二者没有差别(见公式1&2),但是,从实现方面来看,k点的point-wise conventions相当于用了k个卷积核而k组的group point-wise convention只用了一个卷积核,因此group point-wise convention更利于实现。经过如上的改动所获得的Unit,称之为EESP Unit。
d = N k (1) d=\frac{N}{k}\tag{1} d=kN(1)
∴ d 2 ⋅ k = N ⋅ d , N k ⋅ N k ⋅ k = N ⋅ d (2) \therefore\, d^2\cdot k=N\cdot d,\;\frac{N}{k}\cdot \frac{N}{k}\cdot k=N\cdot d\tag{2} ∴d2⋅k=N⋅d,kN⋅kN⋅k=N⋅d(2)
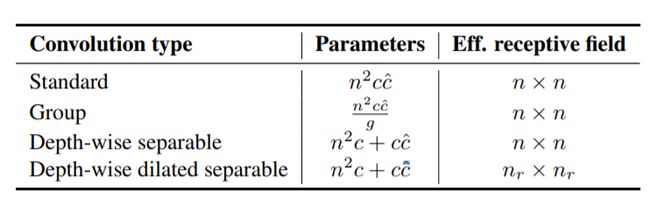
上图表示的是论文中涉及的几种卷积层对应的参数量以及其感知域的对比,从中可见,EESP应用的深度空洞可分离卷积具有最少的参数和最大的感受野。
最后为了直观的表示参数量,我们对所有网络进行实例对比:
当n=3,N=M=128,K=4时,根据本例子对参数量进行计算:
| 网格 | 传统2D卷积 | 深度可分离卷积 | 分组卷积 | ESPNet | ESPNetv2 |
|---|---|---|---|---|---|
| 参数量 | M*n2*N | n2*1*M+1*1*N*M | n2*(M/K)*(N/K)*K | MN/K + (nN)2/K | (n2*(N/K)+(N/K)2)*K+1*1*(N/K)2*K |
| 大小 | 147456 | 17536 | 36864 | 40960 | 9344 |
由此可以见EESP相较于其他几种卷积方法,在参数量上的确有明显的减少。
3.7 Strided EESP与图像输入快速连接
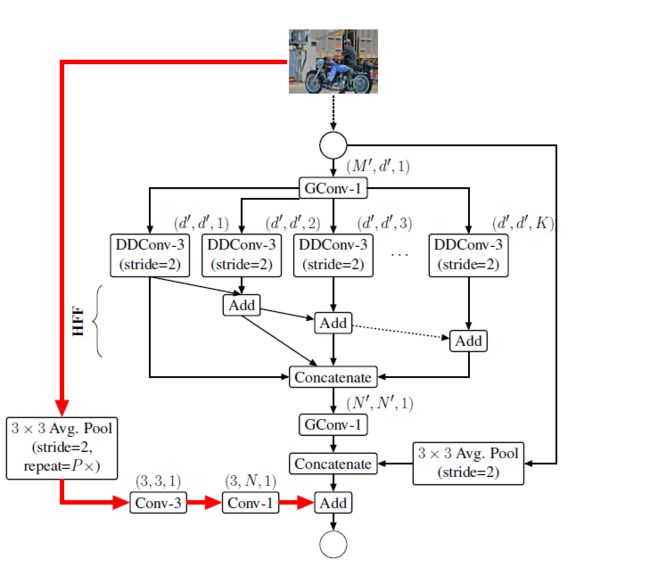
为了在多尺度下能够有效地学习特征,对图1c的网络做了四点改动(如下图所示):
1)对DDConv添加stride属性。
2)右边的shortcut中带了平均池化操作,实现维度匹配。
3)将相加的特征融合方式替换为concat形式,增加特征的维度。
4)融合原始输入图像的下采样信息,使得特征信息更加丰富。具体做法是先将图像下采样到与特征图的尺寸相同的尺寸,然后使用第一个卷积,一个标准的3×3卷积,用于学习空间表示。再使用第二个卷积,一个逐点卷积,用于学习输入之间的线性组合,并将其投影到高维空间。
3.8 ESPNetv2的网络结构
ESPNetv2网络使用EESP单元构建。在每个空间级别,ESPNetv2重复多次EESP单元以增加网络的深度。其中在每个卷积层之后使用batch normalization和PRelu,但在最后一个组级卷积层除外,在该层中,PRelu是在element-wise sum操作之后应用的。
-
Batch normalization
对于每个隐层神经元,把逐渐向非线性函数映射后向取值区间极限饱和区靠拢的输入分布强制拉回到均值为0方差为1的比较标准的正态分布,使得非线性变换函数的输入值落入对输入比较敏感的区域,以此避免梯度消失问题。然而如果只是单纯的把数值拉回0-1正态分布,那就等价于把非线性函数变为线性函数,这就使模型的表示能力变差,失去“深度”的意义。所以BN为了保证非线性的获得,对变换后的满足均值为0方差为1的x又进行了scale加上shift操作(y=scale*x+shift),这样的一番操作之后可以找到一个线性和非线性的较好平衡点,既能享受非线性的较强表达能力的好处,又避免太靠非线性区两头使得网络收敛速度太慢。 -
PRelu(Parametric Rectified Linear Unit)
不同计算复杂度的ESPNet V2网络,用于将224×224输入分类为ImageNet数据集中的1000个类(如下图所示)。

4. 实验
为了展示ESPNetv2的威力,作者在四种任务上与其他网络进行了评估和比较:(1)object classification,(2)semantic segmentation,(3)object detection,(4)language modeling
4.1 图像分类
数据集:
作者用的是ImageNet1000类的数据集,这其中包含着1.28M训练图像和50K验证图像。作者用来评估性能的指标是single crop top-1 classification accuracy
single crop: 先将图像resize到某个大小,比如256xN,然后选择图像正中央部分,比如244x244。
top-1: 对于一个测试图像,模型预测的概率最大的分类是正确分类,才认为是该模型对该图像分类正确
训练:
作者是用搭配CUDA 9.0和cuDNN的PyTorch框架来进行训练的。并且为了优化,使用了热重启的随机梯度下降(SGD with warm restart),即在每个迭代次数(epoch)t时,用这个公式来计算学习率:
η t = η m a x − ( t m o d T ) ⋅ η m i n \eta_t=\eta_{max}-(t\; mod\; T)\,\cdot\, \eta_{min} ηt=ηmax−(tmodT)⋅ηmin
其中 η m a x \eta_{max} ηmax 和 η m i n \eta_{min} ηmin 是学习率变化范围的最大值和最小值, T T T 是学习率重启的循环周期。通过下图我们能很清晰地看出学习率是如何变化的:

作者在实验中设置 η m a x = 0.1 \eta_{max}=0.1 ηmax=0.1, η m i n = 0.5 \eta_{min}=0.5 ηmin=0.5, T = 5 T=5 T=5, batch size设置为512,训练300个epoch,使用交叉熵损失函数。并且为了快速收敛,在以下epoch的时候将学习率减半:{ 50,100,130,160,190,220,250,280 }。数据增强用的是标准的数据增强策略(除了color-based normalization没有用),这与最近的轻量级架构形成了对比,后者用了更少的scale augmentation来防止欠拟合。初始化网络权重的方法是用的何恺明大佬的方法(引用的这个论文:Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification)
结果:
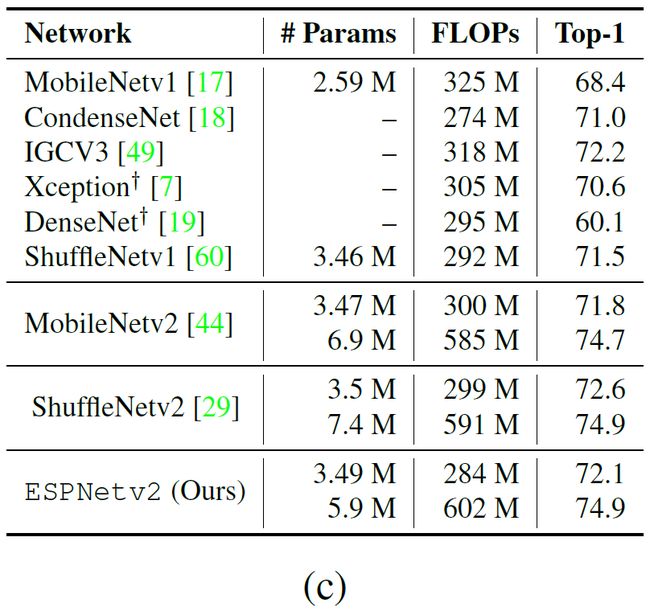
如图所示是ESPNetv2与其他最先进的轻量级网络的性能对比:

- 跟ShuffleNetv1一样,ESPNetv2也使用了逐点群卷积(group point-wise convolution),但没有用在ShuffleNetv1里很有效的 通道混洗(channel shuffle),却达到了比ShuffleNetv1更好的性能。(言外之意:我没用这个trick我就这么nb了┗|`O′|┛ 嗷~~)
- 跟MobileNet相比,ESPNetv2也达到了更好的性能,尤其是在小计算开销的情况下。在28百万FLOPs时,ESPNetv2的性能比MobileNetv1(34百万FLOPs)好10%,比MobileNetv2(30百万FLOPs)好2%。
- ESPNetv2达到了堪比ShuffleNetv2的准确率,但却没有使用通道分片(channel split),而正是这个trick使得ShuffleNetv2比ShuffleNetv1拥有更好的性能。所以作者相信如果用上了这两个trick(channel shuffle,channel split),可以使网络更加轻量,准确率更高。(无形装逼最为致命w(゚Д゚)w)
- 和其他轻量级网络比,在300百万FLOPs的计算开销下,ESPNetv2性能更好,比如:比CondenseNet准确率高1.1%。(就是吊打你们(´ー∀ー`))
多标签分类:
为了评估在迁移学习中的泛化能力,作者在MSCOCO的多目标分类任务上对我们的模型进行评估。作者是在验证集(40504张图像)上使用F1分数(F1 score)进行评估的。作者微调(finetune)了ESPNetv2(284百万FLOPs)和ShuffleNetv2(299百万FLOPs)到100个迭代次数,并且使用和训练ImageNet数据集时一样的数据增强和训练设置,除了一点不一样: η m a x = 0.005 \eta_{max}=0.005 ηmax=0.005, η m i n = 0.001 \eta_{min}=0.001 ηmin=0.001,并且学习率在50和80个epoch的时候减半。使用二元交叉熵损失函数来进行优化。结果如下图所示:
性能分析:
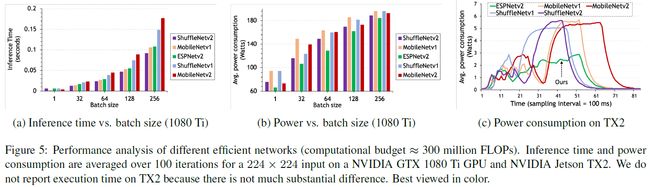
边缘设备的计算资源和能源开销都比较有限。为这种设备设计的轻量级网络应该达到更少的能量消耗,更小的延迟并保持着高准确率。作者又拿出了MobileNet和ShuffleNet进行比较(这俩网络好惨(*゜—゜*)),在以下两种设备上进行测试:(1)高端显卡(NVIDIA GTX 1080 Ti)(2)嵌入式设备(NVIDIA Jetson TX2)。为了公平比较,作者使用PyTorch作为深度学习框架。下面两张图第一张图比较了推理时间和功耗,第二张图比较了网络的复杂性和准确性:
ESPNetv2的推断速度比最快的网络(ShuffleNetv2)要略微慢一些,在两台设备上都是这样,但是它在保持相似的准确率的同时却更省电。(吊打的心永不变┑( ̄Д  ̄)┍)这说明ESPNetv2在准确率、能源消耗和延迟之间有着很好的tradeoff。对于任何运行在边缘设备上的网络,这是一个非常理想的特性。
4.2 语义分割
数据集:
作者在两个数据集上进行性能评估,分别是Cityscapes和PASCAL VOC 2012数据集。
训练:
作者分两步来训练网络。第一步,用小分辨率的图像进行训练(PASCAL VOC 2012的256x256,CityScapes的512x256),用随机梯度下降对网络进行100个epoch的训练,初始学习率设置为0.007。第二步,提高图像分辨率(PASCAL VOC 2012的384x384,CityScapes的1024x512)然后微调ESPNetv2到1000个epoch,用初始学习率为0.003的随机梯度下降并且使用之前提到的循环学习率策略。在最开始的50个epoch,循环周期设为5,之后的设为50.我们用平均交并比(mean intersection over union)作为指标评估准确率。为了评估,我们使用最近邻插值将分割后的mask上采样到与输入图像相同的大小。
结果:
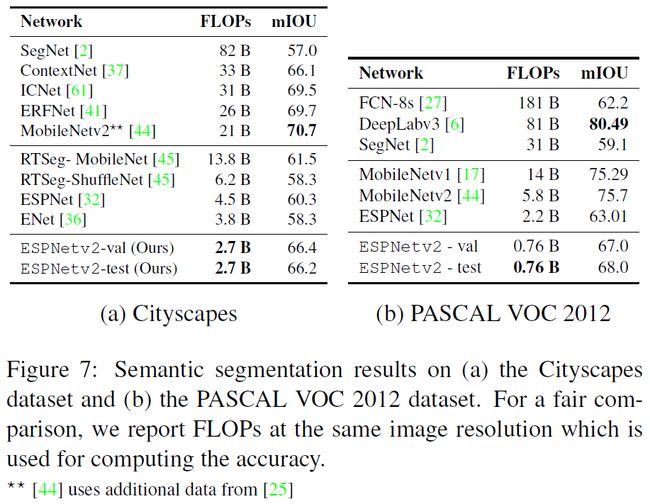
作者在CityScapes和PASCAL VOC 2012这两个数据集上比较了ESPNetv2与其他最先进的网络的性能,如下图所示:
作者说可以看出ESPNetv2的性能与其他网络相比还是很有竞争力的,但却更轻量。在同等的算力条件下,ESPNetv2比现存的网络(比如ENet,ESPNet)nb了一大截。值得注意的是,ESPNetv2的准确率比ICNet、ERFNet和ContextNet等其他网络要低2-3%,但是它FLOPs要低了9-12倍。(总而言之就是NB<(ˉ^ˉ)>)
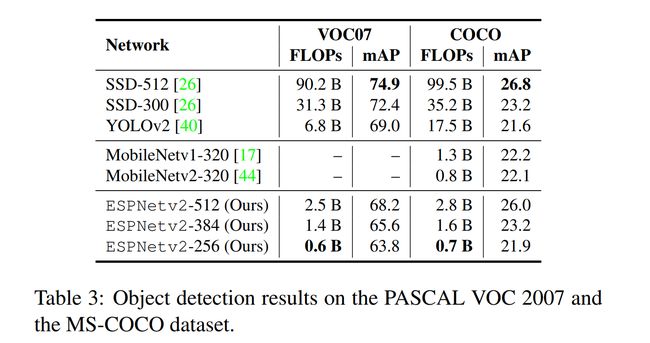
4.3 目标检测
为了探究ESPNetV2在目标检测任务上的表现,作者用ESPNetV2替换掉了SSD(Single Shot Detector)中所利用的VGG,并分别在PASCAL VOC2007和COCO数据集上进行测试。通过表3可以发现,ESPNetv2比较好地权衡了效能和精确度这两个评估标准。相较于传统利用VGG16的SSD,新SSD取得了非常大的效能的提升。即使与YOLO9000进行对比,用ESPNetv2替换VGG16的SSD在效能上也有可观的提升。
4.4 语言建模
这个不是我们研究的主要方向,就偷个懒了(ヽ(✿゚▽゚)ノ)
5 消融实验
这一部分对ESPNetv2中所应用的一些trick进行对照实验
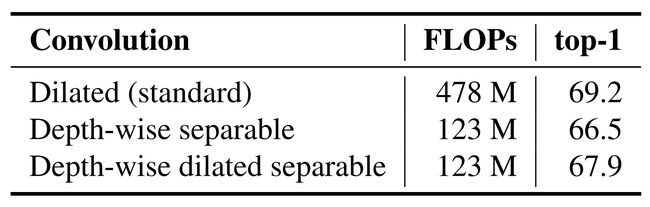
5.1 Convolution
这一部分验证了深度可分离空洞卷积的作用。作者分别将深度可分离空洞卷积替换至深度可分离卷积和标准的空洞卷积并进行效能和准确率的测试。试验结果表明,相较于深度可分离卷积,深度可分离空洞卷积提升了准确率,但由于两种方法所需要的参数一样,所以FLOPs并没有发生变化。相较于标准的空洞卷积,深度可分离空洞卷积大大减少了FLOPs( n 2 N 2 K → ( n 2 N K + N 2 K 2 ) × K \frac{n^2N^2}{K}\to \left( \frac{n^2N}{K}+\frac{N^2}{K^2}\right)\times K Kn2N2→(Kn2N+K2N2)×K )
5.2 HFF
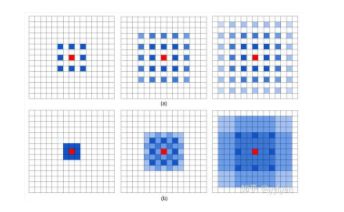
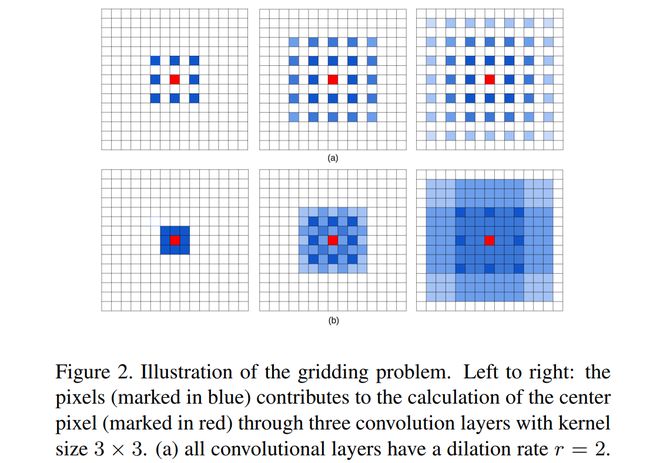
HFF这一结构是在ESPNet中提出来的,ESPNetv2延用了这一设计。这一设计的目的是为了解决由空洞卷积引发的著名的gridding artifact问题。下面的一幅图表示了什么是gridding:
上图(a)代表着三个空洞卷积层,它们的卷积核的大小都是 3 ∗ 3 3*3 3∗3。可以看出,左图中的红色像素是由最上层的9个像素计算来的,而这9个像素映射到底层(即最右图所示)是由这 7 ∗ 7 7*7 7∗7个像素计算得到的。虽然空洞卷积可以在相同的卷积核大小下获得更大的感受野,但是当空洞率越大,则对输入的采样越稀疏,一些局部信息也因此而丢失;并且长距离间隔的信息可能并不相关,打断了局部信息之间的连续性特征,下图中的中间一行即表明了gridding所造成的影响。
现今消除gridding artifact的方法大多需要比较多的运算参数(比如添加新的卷积层),而HFF只是进行简单的矩阵运算,在一定程度上消除了高空洞率所引起的采样稀疏问题,更满足ESPNet减少参数和运算的设计要求。下图展示了HFF去除gridding artifact的效果。通过对比实验,还能发现HFF提升了分类的精准度,这是因为多个分支不同感受野的卷积结果通过HFF共享信息,学习到了更丰富的特征。
5.3 Shortcut connection
Shortcut结构帮助缓解在卷积过程中下采样造成的信息丢失,可以使一个卷积单元学到更多的特征,通过实验对比,Shortcut结构提升了Top1 准确率。
5.4 Cyclic learning
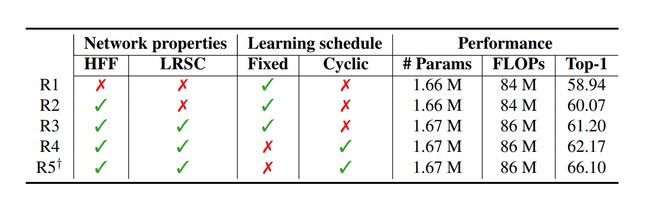
作者在4.1节的图像分类实验中,提到了本文所使用的周期学习策略(cyclic learning rate)。以往的策略是设置一个初始学习率,然后令其逐步减小直到损失函数不再下降。Cyclical Learning Rate则是在一个合理范围内进行周期变化,这样在大多数情况下都可以得到一个接近最优学习率的学习率。如下图所示,当变化区间设置的足够合理时,相当于能以更少的步骤提高模型的准确率,即提升模型的收敛速度。
表中R3的实验是利用固定学习率的策略(初始学习率为0.1,总共训练90个epoch,每过30个epoch学习率衰减1/10),R4的实验则是利用cyclic learning rate的策略,与R3的区别是每个周期内学习率在区间0.1-0.5之间波动,实验结果表明循环学习的策略在0.1和0.5之间找到了一个更好的局部最小值。R5则是利用4.1节的训练方法(cyclic learning rate,总共300个epoch),相较于R4,R5对R3的Top1准确率提升更为明显。
6 总结
本文介绍了一种轻权重、低功耗的网络ESPNetv2,它能更好地对图像中的空间信息进行编码。这个网络是一个通用的网络,具有良好的泛化能力,可以用于广泛的任务,包括序列建模。这个网络在不同的任务(如对象分类、检测、分割和语言建模)中提供了最先进的性能,同时更节能。
7 代码
在这里我们对核心代码 EESP 模块进行一下解释
from torch.nn import init
import torch.nn.functional as F
from cnn.cnn_utils import *
import math
import torch
__author__ = "Sachin Mehta"
__version__ = "1.0.1"
__maintainer__ = "Sachin Mehta"
class EESP(nn.Module):
'''
EESP类定义了两个函数,初始化函数和前向传播,前向传播按照
REDUCE ---> SPLIT ---> TRANSFORM --> MERGE
进行运算
'''
def __init__(self, nIn, nOut, stride=1, k=4, r_lim=7, down_method='esp'): #down_method --> ['avg' or 'esp']
'''
:param nIn: number of input channels 输入通道数
:param nOut: number of output channels 输出通道数
:param stride: factor by which we should skip (useful for down-sampling). If 2, then down-samples the feature map by 2 步长
:param k: # of parallel branches 并行卷积的分支个数
:param r_lim: A maximum value of receptive field allowed for EESP block EESP模块的最大感受野
:param g: number of groups to be used in the feature map reduction step. 分组卷积的参数
'''
super().__init__()
self.stride = stride#初始化步长
n = int(nOut / k)
n1 = nOut - (k - 1) * n
assert down_method in ['avg', 'esp'], 'One of these is suppported (avg or esp)'
assert n == n1, "n(={}) and n1(={}) should be equal for Depth-wise Convolution ".format(n, n1)#分支深度卷积中,膨胀率最大时的维度要和输出维度相同
self.proj_1x1 = CBR(nIn, n, 1, stride=1, groups=k)#初始化2D卷积,然后归一化,再用PRELU去线性化
map_receptive_ksize = {3: 1, 5: 2, 7: 3, 9: 4, 11: 5, 13: 6, 15: 7, 17: 8}#对3*3卷积核,膨胀率和膨胀卷积核大小之间的对应关系
self.k_sizes = list()
for i in range(k):#膨胀率和膨胀卷积核大小之间的对应关系
ksize = int(3 + 2 * i)
# 到达边界后
ksize = ksize if ksize <= r_lim else 3
self.k_sizes.append(ksize)
self.k_sizes.sort()
self.spp_dw = nn.ModuleList()
for i in range(k):#初始化膨胀卷积函数
#Transform
d_rate = map_receptive_ksize[self.k_sizes[i]]#每轮的膨胀率
self.spp_dw.append(CDilated(n, n, kSize=3, stride=stride, groups=n, d=d_rate))#将所有分支的膨胀函数装到spp_dw中
self.conv_1x1_exp = CB(nOut, nOut, 1, 1, groups=k)#卷积操作后归一化
self.br_after_cat = BR(nOut)#规范化,BR函数为PRELU和归一化
self.module_act = nn.PReLU(nOut)#去线性化
self.downAvg = True if down_method == 'avg' else False
def forward(self, input): "前向传播算法"
# Reduce,将M维输入降维到D=N/K维
output1 = self.proj_1x1(input)
output = [self.spp_dw[0](output1)]
# 计算每个分支的输出并依次融合
# Split --> Transform --> HFF
for k in range(1, len(self.spp_dw)):
out_k = self.spp_dw[k](output1)#每个分支进行DDConv
# HFF,从最小的膨胀卷积核的输出开始,逐级叠加,为了改善网格效应
out_k = out_k + output[k - 1]
#保存下来每个分支的结果再融合
output.append(out_k)
# Merge
expanded = self.conv_1x1_exp( # 先将输出拼接
self.br_after_cat( # 然后规范化
torch.cat(output, 1) # 使用1*1的卷积核进行2d卷积操作,再归一化
)
)
del output
# 步长为二,下采样,输出变小
if self.stride == 2 and self.downAvg:
return expanded
# 如果输入和输出向量的维度相同,则加和再输出
if expanded.size() == input.size():
expanded = expanded + input
return self.module_act(expanded)