scikit-learn_Scikit Learn-快速指南
scikit-learn
Scikit Learn-快速指南 (Scikit Learn - Quick Guide)
Scikit Learn-简介 (Scikit Learn - Introduction)
In this chapter, we will understand what is Scikit-Learn or Sklearn, origin of Scikit-Learn and some other related topics such as communities and contributors responsible for development and maintenance of Scikit-Learn, its prerequisites, installation and its features.
在本章中,我们将了解什么是Scikit-Learn或Sklearn,Scikit-Learn的起源以及其他一些相关主题,例如负责Scikit-Learn的开发和维护的社区和贡献者,其先决条件,安装及其功能。
什么是Scikit-Learn(Sklearn) (What is Scikit-Learn (Sklearn))
Scikit-learn (Sklearn) is the most useful and robust library for machine learning in Python. It provides a selection of efficient tools for machine learning and statistical modeling including classification, regression, clustering and dimensionality reduction via a consistence interface in Python. This library, which is largely written in Python, is built upon NumPy, SciPy and Matplotlib.
Scikit-learn(Sklearn)是用于Python中机器学习的最有用和最强大的库。 它通过Python中的一致性接口为机器学习和统计建模提供了一系列有效的工具,包括分类,回归,聚类和降维。 该库主要用Python编写,基于NumPy,SciPy和Matplotlib构建 。
Scikit-Learn的起源 (Origin of Scikit-Learn)
It was originally called scikits.learn and was initially developed by David Cournapeau as a Google summer of code project in 2007. Later, in 2010, Fabian Pedregosa, Gael Varoquaux, Alexandre Gramfort, and Vincent Michel, from FIRCA (French Institute for Research in Computer Science and Automation), took this project at another level and made the first public release (v0.1 beta) on 1st Feb. 2010.
它最初称为scikits.learn ,最初由David Cournapeau于2007年在Google的夏季代码项目中开发。后来,在2010年,FIRCA(法国研究学院)的Fabian Pedregosa,Gael Varoquaux,Alexandre Gramfort和Vincent Michel计算机科学与自动化),将这个项目带入了另一个层次,并于2010年2月1日发布了第一个公开版本(v0.1 beta)。
Let’s have a look at its version history −
让我们看看它的版本历史-
May 2019: scikit-learn 0.21.0
2019年5月:scikit-learn 0.21.0
March 2019: scikit-learn 0.20.3
2019年3月:scikit-learn 0.20.3
December 2018: scikit-learn 0.20.2
2018年12月:scikit-learn 0.20.2
November 2018: scikit-learn 0.20.1
2018年11月:scikit-learn 0.20.1
September 2018: scikit-learn 0.20.0
2018年9月:scikit-learn 0.20.0
July 2018: scikit-learn 0.19.2
2018年7月:scikit-learn 0.19.2
July 2017: scikit-learn 0.19.0
2017年7月:scikit-learn 0.19.0
September 2016. scikit-learn 0.18.0
2016年9月。scikit-learn 0.18.0
November 2015. scikit-learn 0.17.0
2015年11月。scikit-learn 0.17.0
March 2015. scikit-learn 0.16.0
2015年3月。scikit-learn 0.16.0
July 2014. scikit-learn 0.15.0
2014年7月。scikit-learn 0.15.0
August 2013. scikit-learn 0.14
2013年8月。scikit-learn 0.14
社区和贡献者 (Community & contributors)
Scikit-learn is a community effort and anyone can contribute to it. This project is hosted on https://github.com/scikit-learn/scikit-learn. Following people are currently the core contributors to Sklearn’s development and maintenance −
Scikit-learn是一项社区活动,任何人都可以为此做出贡献。 该项目托管在https://github.com/scikit-learn/scikit-learn上。 目前,以下人员是Sklearn开发和维护的主要贡献者-
Joris Van den Bossche (Data Scientist)
Joris Van den Bossche(数据科学家)
Thomas J Fan (Software Developer)
Thomas J Fan(软件开发人员)
Alexandre Gramfort (Machine Learning Researcher)
Alexandre Gramfort(机器学习研究员)
Olivier Grisel (Machine Learning Expert)
Olivier Grisel(机器学习专家)
Nicolas Hug (Associate Research Scientist)
Nicolas Hug(副研究员)
Andreas Mueller (Machine Learning Scientist)
Andreas Mueller(机器学习科学家)
Hanmin Qin (Software Engineer)
秦汉民(软件工程师)
Adrin Jalali (Open Source Developer)
Adrin Jalali(开源开发人员)
Nelle Varoquaux (Data Science Researcher)
Nelle Varoquaux(数据科学研究员)
Roman Yurchak (Data Scientist)
Roman Yurchak(数据科学家)
Various organisations like Booking.com, JP Morgan, Evernote, Inria, AWeber, Spotify and many more are using Sklearn.
像Booking.com,JP Morgan,Evernote,Inria,AWeber,Spotify等各种组织都在使用Sklearn。
先决条件 (Prerequisites)
Before we start using scikit-learn latest release, we require the following −
在开始使用scikit-learn最新版本之前,我们需要满足以下条件-
Python (>=3.5)
Python(> = 3.5)
NumPy (>= 1.11.0)
NumPy(> = 1.11.0)
Scipy (>= 0.17.0)li
西皮(> = 0.17.0)li
Joblib (>= 0.11)
Joblib(> = 0.11)
Matplotlib (>= 1.5.1) is required for Sklearn plotting capabilities.
Sklearn绘图功能需要Matplotlib(> = 1.5.1)。
Pandas (>= 0.18.0) is required for some of the scikit-learn examples using data structure and analysis.
使用数据结构和分析的某些scikit学习示例需要使用Pandas(> = 0.18.0)。
安装 (Installation)
If you already installed NumPy and Scipy, following are the two easiest ways to install scikit-learn −
如果您已经安装了NumPy和Scipy,则以下是安装scikit-learn的两种最简单的方法-
使用点 (Using pip)
Following command can be used to install scikit-learn via pip −
以下命令可用于通过pip安装scikit-learn-
pip install -U scikit-learn
使用conda (Using conda)
Following command can be used to install scikit-learn via conda −
以下命令可用于通过conda安装scikit-learn-
conda install scikit-learn
On the other hand, if NumPy and Scipy is not yet installed on your Python workstation then, you can install them by using either pip or conda.
另一方面,如果Python工作站上尚未安装NumPy和Scipy,则可以使用pip或conda进行安装 。
Another option to use scikit-learn is to use Python distributions like Canopy and Anaconda because they both ship the latest version of scikit-learn.
使用scikit-learn的另一种方法是使用Canopy和Anaconda之类的Python发行版,因为它们都提供了最新版本的scikit-learn。
特征 (Features)
Rather than focusing on loading, manipulating and summarising data, Scikit-learn library is focused on modeling the data. Some of the most popular groups of models provided by Sklearn are as follows −
Scikit-learn库不是专注于加载,处理和汇总数据,而是专注于对数据建模。 Sklearn提供的一些最受欢迎的模型组如下-
Supervised Learning algorithms − Almost all the popular supervised learning algorithms, like Linear Regression, Support Vector Machine (SVM), Decision Tree etc., are the part of scikit-learn.
监督学习算法 -几乎所有流行的监督学习算法,例如线性回归,支持向量机(SVM),决策树等,都是scikit-learn的一部分。
Unsupervised Learning algorithms − On the other hand, it also has all the popular unsupervised learning algorithms from clustering, factor analysis, PCA (Principal Component Analysis) to unsupervised neural networks.
无监督学习算法 -另一方面,它也具有从聚类,因子分析,PCA(主成分分析)到无监督神经网络的所有流行的无监督学习算法。
Clustering − This model is used for grouping unlabeled data.
群集 -此模型用于对未标记的数据进行分组。
Cross Validation − It is used to check the accuracy of supervised models on unseen data.
交叉验证 -用于检查看不见的数据上监督模型的准确性。
Dimensionality Reduction − It is used for reducing the number of attributes in data which can be further used for summarisation, visualisation and feature selection.
降维 -用于减少数据中的属性数量,这些属性可进一步用于汇总,可视化和特征选择。
Ensemble methods − As name suggest, it is used for combining the predictions of multiple supervised models.
集成方法 -顾名思义,它用于组合多个监督模型的预测。
Feature extraction − It is used to extract the features from data to define the attributes in image and text data.
特征提取 -用于从数据中提取特征,以定义图像和文本数据中的属性。
Feature selection − It is used to identify useful attributes to create supervised models.
特征选择 -用于识别有用的属性以创建监督模型。
Open Source − It is open source library and also commercially usable under BSD license.
开源 -它是开源库,并且在BSD许可下也可以商业使用。
Scikit学习-建模过程 (Scikit Learn - Modelling Process)
This chapter deals with the modelling process involved in Sklearn. Let us understand about the same in detail and begin with dataset loading.
本章介绍Sklearn中涉及的建模过程。 让我们详细了解一下,并从数据集加载开始。
数据集加载 (Dataset Loading)
A collection of data is called dataset. It is having the following two components −
数据的集合称为数据集。 它具有以下两个组成部分-
Features − The variables of data are called its features. They are also known as predictors, inputs or attributes.
特征 -数据的变量称为其特征。 它们也称为预测变量,输入或属性。
Feature matrix − It is the collection of features, in case there are more than one.
特征矩阵 -如果有多个特征,它是特征的集合。
Feature Names − It is the list of all the names of the features.
功能名称 -这是所有功能名称的列表。
Response − It is the output variable that basically depends upon the feature variables. They are also known as target, label or output.
响应 -基本取决于特征变量的是输出变量。 它们也称为目标,标签或输出。
Response Vector − It is used to represent response column. Generally, we have just one response column.
响应向量 -用于表示响应列。 通常,我们只有一个响应列。
Target Names − It represent the possible values taken by a response vector.
目标名称 -它表示响应向量可能采用的值。
Scikit-learn have few example datasets like iris and digits for classification and the Boston house prices for regression.
Scikit-learn几乎没有示例数据集,例如用于分类的虹膜和数字 ,以及用于回归的波士顿房价 。
例 (Example)
Following is an example to load iris dataset −
以下是加载虹膜数据集的示例-
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
target_names = iris.target_names
print("Feature names:", feature_names)
print("Target names:", target_names)
print("\nFirst 10 rows of X:\n", X[:10])
输出量 (Output)
Feature names: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
Target names: ['setosa' 'versicolor' 'virginica']
First 10 rows of X:
[
[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]
[5.4 3.9 1.7 0.4]
[4.6 3.4 1.4 0.3]
[5. 3.4 1.5 0.2]
[4.4 2.9 1.4 0.2]
[4.9 3.1 1.5 0.1]
]
分割数据集 (Splitting the dataset)
To check the accuracy of our model, we can split the dataset into two pieces-a training set and a testing set. Use the training set to train the model and testing set to test the model. After that, we can evaluate how well our model did.
为了检查模型的准确性,我们可以将数据集分为两部分:训练集和测试集 。 使用训练集训练模型,并使用测试集测试模型。 之后,我们可以评估模型的效果。
例 (Example)
The following example will split the data into 70:30 ratio, i.e. 70% data will be used as training data and 30% will be used as testing data. The dataset is iris dataset as in above example.
以下示例将数据分成70:30的比例,即70%的数据将用作训练数据,而30%的数据将用作测试数据。 数据集是虹膜数据集,如上例所示。
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size = 0.3, random_state = 1
)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
输出量 (Output)
(105, 4)
(45, 4)
(105,)
(45,)
As seen in the example above, it uses train_test_split() function of scikit-learn to split the dataset. This function has the following arguments −
如上例所示,它使用scikit-learn的train_test_split()函数来拆分数据集。 此函数具有以下参数-
X, y − Here, X is the feature matrix and y is the response vector, which need to be split.
X,y-在这里, X是特征矩阵 ,y是响应向量 ,需要进行拆分。
test_size − This represents the ratio of test data to the total given data. As in the above example, we are setting test_data = 0.3 for 150 rows of X. It will produce test data of 150*0.3 = 45 rows.
test_size-这表示测试数据与总给定数据的比率。 如上例所示,我们为150行X设置了test_data = 0.3 。它将产生150 * 0.3 = 45行的测试数据。
random_size − It is used to guarantee that the split will always be the same. This is useful in the situations where you want reproducible results.
random_size-用于确保拆分将始终相同。 在需要可重现结果的情况下,这很有用。
训练模型 (Train the Model)
Next, we can use our dataset to train some prediction-model. As discussed, scikit-learn has wide range of Machine Learning (ML) algorithms which have a consistent interface for fitting, predicting accuracy, recall etc.
接下来,我们可以使用我们的数据集来训练一些预测模型。 正如讨论的那样,scikit-learn具有广泛的机器学习(ML)算法 ,这些算法具有一致的接口,可以进行拟合,预测准确性,召回率等。
例 (Example)
In the example below, we are going to use KNN (K nearest neighbors) classifier. Don’t go into the details of KNN algorithms, as there will be a separate chapter for that. This example is used to make you understand the implementation part only.
在下面的示例中,我们将使用KNN(K个最近邻居)分类器。 无需赘述KNN算法的细节,因为将有单独的章节。 本示例仅用于使您理解实现部分。
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size = 0.4, random_state=1
)
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
classifier_knn = KNeighborsClassifier(n_neighbors = 3)
classifier_knn.fit(X_train, y_train)
y_pred = classifier_knn.predict(X_test)
# Finding accuracy by comparing actual response values(y_test)with predicted response value(y_pred)
print("Accuracy:", metrics.accuracy_score(y_test, y_pred))
# Providing sample data and the model will make prediction out of that data
sample = [[5, 5, 3, 2], [2, 4, 3, 5]]
preds = classifier_knn.predict(sample)
pred_species = [iris.target_names[p] for p in preds] print("Predictions:", pred_species)
输出量 (Output)
Accuracy: 0.9833333333333333
Predictions: ['versicolor', 'virginica']
模型持久性 (Model Persistence)
Once you train the model, it is desirable that the model should be persist for future use so that we do not need to retrain it again and again. It can be done with the help of dump and load features of joblib package.
训练完模型后,最好保留模型以备将来使用,这样我们就不必一次又一次地重新训练它。 可以借助joblib软件包的转储和加载功能来完成 。
Consider the example below in which we will be saving the above trained model (classifier_knn) for future use −
考虑下面的示例,在该示例中,我们将保存以上训练的模型(classifier_knn)供以后使用-
from sklearn.externals import joblib
joblib.dump(classifier_knn, 'iris_classifier_knn.joblib')
The above code will save the model into file named iris_classifier_knn.joblib. Now, the object can be reloaded from the file with the help of following code −
上面的代码会将模型保存到名为iris_classifier_knn.joblib的文件中。 现在,可以在以下代码的帮助下从文件中重新加载对象:
joblib.load('iris_classifier_knn.joblib')
预处理数据 (Preprocessing the Data)
As we are dealing with lots of data and that data is in raw form, before inputting that data to machine learning algorithms, we need to convert it into meaningful data. This process is called preprocessing the data. Scikit-learn has package named preprocessing for this purpose. The preprocessing package has the following techniques −
由于我们要处理大量数据,并且这些数据是原始格式,因此在将该数据输入到机器学习算法之前,我们需要将其转换为有意义的数据。 此过程称为预处理数据。 为此,Scikit-learn具有名为预处理的软件包。 预处理程序包具有以下技术-
二值化 (Binarisation)
This preprocessing technique is used when we need to convert our numerical values into Boolean values.
当我们需要将数值转换为布尔值时,可以使用这种预处理技术。
例 (Example)
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]]
)
data_binarized = preprocessing.Binarizer(threshold=0.5).transform(input_data)
print("\nBinarized data:\n", data_binarized)
In the above example, we used threshold value = 0.5 and that is why, all the values above 0.5 would be converted to 1, and all the values below 0.5 would be converted to 0.
在上面的示例中,我们使用阈值 = 0.5,这就是为什么将所有大于0.5的值都转换为1,而将所有小于0.5的值都转换为0的原因。
输出量 (Output)
Binarized data:
[
[ 1. 0. 1.]
[ 0. 1. 1.]
[ 0. 0. 1.]
[ 1. 1. 0.]
]
均值去除 (Mean Removal)
This technique is used to eliminate the mean from feature vector so that every feature centered on zero.
该技术用于消除特征向量的均值,以便每个特征都以零为中心。
例 (Example)
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]]
)
#displaying the mean and the standard deviation of the input data
print("Mean =", input_data.mean(axis=0))
print("Stddeviation = ", input_data.std(axis=0))
#Removing the mean and the standard deviation of the input data
data_scaled = preprocessing.scale(input_data)
print("Mean_removed =", data_scaled.mean(axis=0))
print("Stddeviation_removed =", data_scaled.std(axis=0))
输出量 (Output)
Mean = [ 1.75 -1.275 2.2 ]
Stddeviation = [ 2.71431391 4.20022321 4.69414529]
Mean_removed = [ 1.11022302e-16 0.00000000e+00 0.00000000e+00]
Stddeviation_removed = [ 1. 1. 1.]
缩放比例 (Scaling)
We use this preprocessing technique for scaling the feature vectors. Scaling of feature vectors is important, because the features should not be synthetically large or small.
我们使用这种预处理技术来缩放特征向量。 特征向量的缩放很重要,因为特征不应该合成的大或小。
例 (Example)
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_scaler_minmax = preprocessing.MinMaxScaler(feature_range=(0,1))
data_scaled_minmax = data_scaler_minmax.fit_transform(input_data)
print ("\nMin max scaled data:\n", data_scaled_minmax)
输出量 (Output)
Min max scaled data:
[
[ 0.48648649 0.58252427 0.99122807]
[ 0. 1. 0.81578947]
[ 0.27027027 0. 1. ]
[ 1. 0.99029126 0. ]
]
正常化 (Normalisation)
We use this preprocessing technique for modifying the feature vectors. Normalisation of feature vectors is necessary so that the feature vectors can be measured at common scale. There are two types of normalisation as follows −
我们使用这种预处理技术来修改特征向量。 特征向量的归一化是必要的,以便可以在公共尺度上测量特征向量。 标准化有以下两种类型-
L1归一化 (L1 Normalisation)
It is also called Least Absolute Deviations. It modifies the value in such a manner that the sum of the absolute values remains always up to 1 in each row. Following example shows the implementation of L1 normalisation on input data.
也称为最小绝对偏差。 它以使绝对值的总和在每一行中始终保持最大为1的方式修改值。 以下示例显示了对输入数据进行L1标准化的实现。
例 (Example)
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_normalized_l1 = preprocessing.normalize(input_data, norm='l1')
print("\nL1 normalized data:\n", data_normalized_l1)
输出量 (Output)
L1 normalized data:
[
[ 0.22105263 -0.2 0.57894737]
[-0.2027027 0.32432432 0.47297297]
[ 0.03571429 -0.56428571 0.4 ]
[ 0.42142857 0.16428571 -0.41428571]
]
L2归一化 (L2 Normalisation)
Also called Least Squares. It modifies the value in such a manner that the sum of the squares remains always up to 1 in each row. Following example shows the implementation of L2 normalisation on input data.
也称为最小二乘。 它以这样的方式修改值,使得平方和在每一行中始终保持最大为1。 以下示例显示了对输入数据进行L2标准化的实现。
例 (Example)
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_normalized_l2 = preprocessing.normalize(input_data, norm='l2')
print("\nL1 normalized data:\n", data_normalized_l2)
输出量 (Output)
L2 normalized data:
[
[ 0.33946114 -0.30713151 0.88906489]
[-0.33325106 0.53320169 0.7775858 ]
[ 0.05156558 -0.81473612 0.57753446]
[ 0.68706914 0.26784051 -0.6754239 ]
]
Scikit学习-数据表示 (Scikit Learn - Data Representation)
As we know that machine learning is about to create model from data. For this purpose, computer must understand the data first. Next, we are going to discuss various ways to represent the data in order to be understood by computer −
众所周知,机器学习即将根据数据创建模型。 为此,计算机必须首先了解数据。 接下来,我们将讨论表示数据的各种方式,以便计算机可以理解-
数据如表 (Data as table)
The best way to represent data in Scikit-learn is in the form of tables. A table represents a 2-D grid of data where rows represent the individual elements of the dataset and the columns represents the quantities related to those individual elements.
在Scikit学习中表示数据的最佳方法是表格。 表格表示数据的二维网格,其中行表示数据集的各个元素,列表示与这些单个元素相关的数量。
例 (Example)
With the example given below, we can download iris dataset in the form of a Pandas DataFrame with the help of python seaborn library.
通过下面给出的示例,我们可以借助python seaborn库以Pandas DataFrame的形式下载虹膜数据集 。
import seaborn as sns
iris = sns.load_dataset('iris')
iris.head()
输出量 (Output)
sepal_length sepal_width petal_length petal_width species
0 5.1 3.5 1.4 0.2 setosa
1 4.9 3.0 1.4 0.2 setosa
2 4.7 3.2 1.3 0.2 setosa
3 4.6 3.1 1.5 0.2 setosa
4 5.0 3.6 1.4 0.2 setosa
From above output, we can see that each row of the data represents a single observed flower and the number of rows represents the total number of flowers in the dataset. Generally, we refer the rows of the matrix as samples.
从上面的输出中,我们可以看到数据的每一行代表一个观察到的花朵,行数代表数据集中的花朵总数。 通常,我们将矩阵的行称为样本。
On the other hand, each column of the data represents a quantitative information describing each sample. Generally, we refer the columns of the matrix as features.
另一方面,数据的每一列代表描述每个样品的定量信息。 通常,我们将矩阵的列称为要素。
数据作为特征矩阵 (Data as Feature Matrix)
Features matrix may be defined as the table layout where information can be thought of as a 2-D matrix. It is stored in a variable named X and assumed to be two dimensional with shape [n_samples, n_features]. Mostly, it is contained in a NumPy array or a Pandas DataFrame. As told earlier, the samples always represent the individual objects described by the dataset and the features represents the distinct observations that describe each sample in a quantitative manner.
特征矩阵可以定义为表格布局,其中信息可以被认为是二维矩阵。 它存储在名为X的变量中,并假定是二维的,形状为[n_samples,n_features]。 通常,它包含在NumPy数组或Pandas DataFrame中。 如前所述,样本始终代表数据集描述的单个对象,而要素代表以定量方式描述每个样本的不同观察结果。
数据作为目标数组 (Data as Target array)
Along with Features matrix, denoted by X, we also have target array. It is also called label. It is denoted by y. The label or target array is usually one-dimensional having length n_samples. It is generally contained in NumPy array or Pandas Series. Target array may have both the values, continuous numerical values and discrete values.
除了用X表示的功能矩阵,我们还有目标数组。 也称为标签。 用y表示。 标签或目标数组通常是一维,长度为n_samples。 它通常包含在NumPy 数组或Pandas 系列中 。 目标数组可以同时具有值,连续数值和离散值。
目标数组与要素列有何不同? (How target array differs from feature columns?)
We can distinguish both by one point that the target array is usually the quantity we want to predict from the data i.e. in statistical terms it is the dependent variable.
我们可以通过一点来区分这两者,即目标数组通常是我们要从数据中预测的数量,即,从统计角度来说,它是因变量。
例 (Example)
In the example below, from iris dataset we predict the species of flower based on the other measurements. In this case, the Species column would be considered as the feature.
在下面的示例中,我们从虹膜数据集中基于其他测量值来预测花朵的种类。 在这种情况下,“种类”列将被视为要素。
import seaborn as sns
iris = sns.load_dataset('iris')
%matplotlib inline
import seaborn as sns; sns.set()
sns.pairplot(iris, hue='species', height=3);
输出量 (Output)
X_iris = iris.drop('species', axis=1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
输出量 (Output)
(150,4)
(150,)
Scikit Learn-估算器API (Scikit Learn - Estimator API)
In this chapter, we will learn about Estimator API (application programming interface). Let us begin by understanding what is an Estimator API.
在本章中,我们将学习Estimator API (应用程序编程接口)。 让我们首先了解什么是Estimator API。
什么是估算器API (What is Estimator API)
It is one of the main APIs implemented by Scikit-learn. It provides a consistent interface for a wide range of ML applications that’s why all machine learning algorithms in Scikit-Learn are implemented via Estimator API. The object that learns from the data (fitting the data) is an estimator. It can be used with any of the algorithms like classification, regression, clustering or even with a transformer, that extracts useful features from raw data.
它是Scikit-learn实现的主要API之一。 它为各种ML应用程序提供了一致的接口,这就是Scikit-Learn中所有机器学习算法都是通过Estimator API实现的原因。 从数据中学习(拟合数据)的对象是估计量。 它可以与分类,回归,聚类的任何算法一起使用,甚至可以与从原始数据中提取有用特征的转换器一起使用。
For fitting the data, all estimator objects expose a fit method that takes a dataset shown as follows −
为了拟合数据,所有估计器对象公开一个fit方法,该方法采用如下所示的数据集:
estimator.fit(data)
Next, all the parameters of an estimator can be set, as follows, when it is instantiated by the corresponding attribute.
接下来,当通过相应的属性实例化估算器时,可以如下设置估算器的所有参数。
estimator = Estimator (param1=1, param2=2)
estimator.param1
The output of the above would be 1.
上面的输出为1。
Once data is fitted with an estimator, parameters are estimated from the data at hand. Now, all the estimated parameters will be the attributes of the estimator object ending by an underscore as follows −
将数据与估算器拟合后,即可根据手头的数据估算参数。 现在,所有估计的参数将成为估计器对象的属性,以下划线结尾,如下所示:
estimator.estimated_param_
估算器API的使用 (Use of Estimator API)
Main uses of estimators are as follows −
估计器的主要用途如下-
模型的估计和解码 (Estimation and decoding of a model)
Estimator object is used for estimation and decoding of a model. Furthermore, the model is estimated as a deterministic function of the following −
估计器对象用于模型的估计和解码。 此外,该模型被估计为以下确定性函数-
The parameters which are provided in object construction.
对象构造中提供的参数。
The global random state (numpy.random) if the estimator’s random_state parameter is set to none.
如果估计器的random_state参数设置为none,则为全局随机状态(numpy.random)。
Any data passed to the most recent call to fit, fit_transform, or fit_predict.
传递给最新调用fit,fit_transform或fit_predict的任何数据。
Any data passed in a sequence of calls to partial_fit.
在对partial_fit的调用序列中传递的任何数据。
将非矩形数据表示映射到矩形数据 (Mapping non-rectangular data representation into rectangular data)
It maps a non-rectangular data representation into rectangular data. In simple words, it takes input where each sample is not represented as an array-like object of fixed length, and producing an array-like object of features for each sample.
它将非矩形数据表示形式映射为矩形数据。 简而言之,它接受输入,其中每个样本都不表示为固定长度的数组状对象,并为每个样本产生特征的数组状对象。
核心样本与外围样本之间的区别 (Distinction between core and outlying samples)
It models the distinction between core and outlying samples by using following methods −
它使用以下方法对核心样本和外围样本之间的区别进行建模-
fit
适合
fit_predict if transductive
fit_predict如果是转导的
predict if inductive
预测是否归纳
指导原则 (Guiding Principles)
While designing the Scikit-Learn API, following guiding principles kept in mind −
在设计Scikit-Learn API时,请牢记以下指导原则-
一致性 (Consistency)
This principle states that all the objects should share a common interface drawn from a limited set of methods. The documentation should also be consistent.
该原则指出,所有对象应该共享从一组有限的方法中提取的公共接口。 文档也应保持一致。
受限的对象层次 (Limited object hierarchy)
This guiding principle says −
这个指导原则说-
Algorithms should be represented by Python classes
算法应由Python类表示
Datasets should be represented in standard format like NumPy arrays, Pandas DataFrames, SciPy sparse matrix.
数据集应以标准格式表示,例如NumPy数组,Pandas DataFrames,SciPy稀疏矩阵。
Parameters names should use standard Python strings.
参数名称应使用标准的Python字符串。
组成 (Composition)
As we know that, ML algorithms can be expressed as the sequence of many fundamental algorithms. Scikit-learn makes use of these fundamental algorithms whenever needed.
众所周知,机器学习算法可以表示为许多基本算法的序列。 Scikit-learn会在需要时使用这些基本算法。
合理的默认值 (Sensible defaults)
According to this principle, the Scikit-learn library defines an appropriate default value whenever ML models require user-specified parameters.
根据此原理,只要ML模型需要用户指定的参数,Scikit-learn库就会定义适当的默认值。
检查 (Inspection)
As per this guiding principle, every specified parameter value is exposed as pubic attributes.
根据此指导原则,每个指定的参数值都公开为公共属性。
使用Estimator API的步骤 (Steps in using Estimator API)
Followings are the steps in using the Scikit-Learn estimator API −
以下是使用Scikit-Learn估计器API的步骤-
步骤1:选择模型类别 (Step 1: Choose a class of model)
In this first step, we need to choose a class of model. It can be done by importing the appropriate Estimator class from Scikit-learn.
在第一步中,我们需要选择一类模型。 可以通过从Scikit-learn导入适当的Estimator类来完成。
步骤2:选择模型超参数 (Step 2: Choose model hyperparameters)
In this step, we need to choose class model hyperparameters. It can be done by instantiating the class with desired values.
在这一步中,我们需要选择类模型超参数。 可以通过用所需的值实例化类来完成。
步骤3:整理资料 (Step 3: Arranging the data)
Next, we need to arrange the data into features matrix (X) and target vector(y).
接下来,我们需要将数据排列到特征矩阵(X)和目标向量(y)中。
步骤4:模型拟合 (Step 4: Model Fitting)
Now, we need to fit the model to your data. It can be done by calling fit() method of the model instance.
现在,我们需要使模型适合您的数据。 可以通过调用模型实例的fit()方法来完成。
步骤5:应用模型 (Step 5: Applying the model)
After fitting the model, we can apply it to new data. For supervised learning, use predict() method to predict the labels for unknown data. While for unsupervised learning, use predict() or transform() to infer properties of the data.
拟合模型后,我们可以将其应用于新数据。 对于监督学习,请使用predict()方法来预测未知数据的标签。 对于无监督学习,请使用predict()或transform()推断数据的属性。
监督学习的例子 (Supervised Learning Example)
Here, as an example of this process we are taking common case of fitting a line to (x,y) data i.e. simple linear regression.
在此,作为此过程的示例,我们以将线拟合到(x,y)数据的简单情况为例,即简单线性回归 。
First, we need to load the dataset, we are using iris dataset −
首先,我们需要加载数据集,我们使用虹膜数据集-
例 (Example)
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
输出量 (Output)
(150, 4)
例 (Example)
y_iris = iris['species']
y_iris.shape
输出量 (Output)
(150,)
例 (Example)
Now, for this regression example, we are going to use the following sample data −
现在,对于此回归示例,我们将使用以下样本数据-
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
输出量 (Output)
So, we have the above data for our linear regression example.
因此,对于线性回归示例,我们具有上述数据。
Now, with this data, we can apply the above-mentioned steps.
现在,利用这些数据,我们可以应用上述步骤。
选择一种型号 (Choose a class of model)
Here, to compute a simple linear regression model, we need to import the linear regression class as follows −
在这里,要计算一个简单的线性回归模型,我们需要导入线性回归类,如下所示:
from sklearn.linear_model import LinearRegression
选择模型超参数 (Choose model hyperparameters)
Once we choose a class of model, we need to make some important choices which are often represented as hyperparameters, or the parameters that must set before the model is fit to data. Here, for this example of linear regression, we would like to fit the intercept by using the fit_intercept hyperparameter as follows −
选择一类模型后,我们需要做出一些重要的选择,这些选择通常表示为超参数,或者是在模型适合数据之前必须设置的参数。 在这里,对于线性回归的示例,我们想通过使用fit_intercept超参数来拟合截距,如下所示:
Example
例
model = LinearRegression(fit_intercept = True)
model
Output
输出量
LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None, normalize = False)
整理数据 (Arranging the data)
Now, as we know that our target variable y is in correct form i.e. a length n_samples array of 1-D. But, we need to reshape the feature matrix X to make it a matrix of size [n_samples, n_features]. It can be done as follows −
现在,我们知道我们的目标变量y的格式正确,即长度为1-D的n_samples数组。 但是,我们需要调整特征矩阵X的 形状,使其成为大小为[n_samples,n_features]的矩阵。 它可以做到如下-
Example
例
X = x[:, np.newaxis]
X.shape
Output
输出量
(40, 1)
模型拟合 (Model fitting)
Once, we arrange the data, it is time to fit the model i.e. to apply our model to data. This can be done with the help of fit() method as follows −
一旦我们整理了数据,就该对模型进行拟合了,即将模型应用于数据。 这可以借助fit()方法完成,如下所示:
Example
例
model.fit(X, y)
Output
输出量
LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None,normalize = False)
In Scikit-learn, the fit() process have some trailing underscores.
在Scikit-learn中, fit()进程带有一些下划线。
For this example, the below parameter shows the slope of the simple linear fit of the data −
对于此示例,以下参数显示了数据的简单线性拟合的斜率-
Example
例
model.coef_
Output
输出量
array([1.99839352])
The below parameter represents the intercept of the simple linear fit to the data −
以下参数表示对数据的简单线性拟合的截距-
Example
例
model.intercept_
Output
输出量
-0.9895459457775022
将模型应用于新数据 (Applying the model to new data)
After training the model, we can apply it to new data. As the main task of supervised machine learning is to evaluate the model based on new data that is not the part of the training set. It can be done with the help of predict() method as follows −
训练模型后,我们可以将其应用于新数据。 监督式机器学习的主要任务是根据不是训练集一部分的新数据评估模型。 可以借助预测()方法完成以下操作-
Example
例
xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);
Output
输出量
完整的工作/可执行示例 (Complete working/executable example)
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
model
X = x[:, np.newaxis]
X.shape
model.fit(X, y)
model.coef_
model.intercept_
xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);
无监督学习示例 (Unsupervised Learning Example)
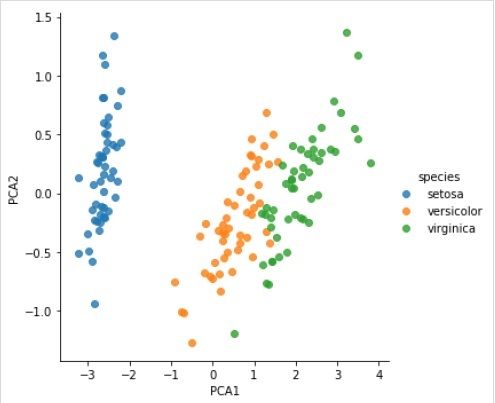
Here, as an example of this process we are taking common case of reducing the dimensionality of the Iris dataset so that we can visualize it more easily. For this example, we are going to use principal component analysis (PCA), a fast-linear dimensionality reduction technique.
在此,作为此过程的示例,我们以降低Iris数据集的维数为例,以便我们可以更轻松地对其进行可视化。 对于此示例,我们将使用主成分分析(PCA),一种快速线性降维技术。
Like the above given example, we can load and plot the random data from iris dataset. After that we can follow the steps as below −
像上面给出的示例一样,我们可以从虹膜数据集中加载并绘制随机数据。 之后,我们可以按照以下步骤操作-
选择一种型号 (Choose a class of model)
from sklearn.decomposition import PCA
选择模型超参数 (Choose model hyperparameters)
Example
例
model = PCA(n_components=2)
model
Output
输出量
PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None,
svd_solver = 'auto', tol = 0.0, whiten = False)
模型拟合 (Model fitting)
Example
例
model.fit(X_iris)
Output
输出量
PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None,
svd_solver = 'auto', tol = 0.0, whiten = False)
将数据转换为二维 (Transform the data to two-dimensional)
Example
例
X_2D = model.transform(X_iris)
Now, we can plot the result as follows −
现在,我们可以将结果绘制如下:
Output
输出量
iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue = 'species', data = iris, fit_reg = False);
Output
输出量
完整的工作/可执行示例 (Complete working/executable example)
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.decomposition import PCA
model = PCA(n_components=2)
model
model.fit(X_iris)
X_2D = model.transform(X_iris)
iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue='species', data=iris, fit_reg=False);
Scikit Learn-约定 (Scikit Learn - Conventions)
Scikit-learn’s objects share a uniform basic API that consists of the following three complementary interfaces −
Scikit-learn的对象共享一个统一的基本API,该API由以下三个互补接口组成-
Estimator interface − It is for building and fitting the models.
估计器接口 -用于构建和拟合模型。
Predictor interface − It is for making predictions.
预测器接口 -用于进行预测。
Transformer interface − It is for converting data.
变压器接口 -用于转换数据。
The APIs adopt simple conventions and the design choices have been guided in a manner to avoid the proliferation of framework code.
这些API采用简单的约定,并且以避免框架代码泛滥的方式指导了设计选择。
公约目的 (Purpose of Conventions)
The purpose of conventions is to make sure that the API stick to the following broad principles −
约定的目的是确保API遵循以下广泛原则-
Consistency − All the objects whether they are basic, or composite must share a consistent interface which further composed of a limited set of methods.
一致性 -所有对象(无论是基础对象还是复合对象)都必须共享一致的接口,该接口进一步由一组有限的方法组成。
Inspection − Constructor parameters and parameters values determined by learning algorithm should be stored and exposed as public attributes.
检查 -构造函数参数和由学习算法确定的参数值应存储并公开为公共属性。
Non-proliferation of classes − Datasets should be represented as NumPy arrays or Scipy sparse matrix whereas hyper-parameters names and values should be represented as standard Python strings to avoid the proliferation of framework code.
类的不扩散 -数据集应表示为NumPy数组或Scipy稀疏矩阵,而超参数名称和值应表示为标准Python字符串,以避免框架代码的泛滥。
Composition − The algorithms whether they are expressible as sequences or combinations of transformations to the data or naturally viewed as meta-algorithms parameterized on other algorithms, should be implemented and composed from existing building blocks.
组合 -无论是将算法表达为数据转换的序列还是转换的组合,或者自然地视为在其他算法上参数化的元算法,都应从现有的构建模块中实施并组成。
Sensible defaults − In scikit-learn whenever an operation requires a user-defined parameter, an appropriate default value is defined. This default value should cause the operation to be performed in a sensible way, for example, giving a base-line solution for the task at hand.
合理的默认值 -在scikit-learn中,每当操作需要用户定义的参数时,就会定义适当的默认值。 此默认值应使操作以明智的方式执行,例如,为手头的任务提供基线解决方案。
各种约定 (Various Conventions)
The conventions available in Sklearn are explained below −
Sklearn中可用的约定在下面进行了解释-
型铸 (Type casting)
It states that the input should be cast to float64. In the following example, in which sklearn.random_projection module used to reduce the dimensionality of the data, will explain it −
它指出输入应强制转换为float64 。 在以下示例中,其中sklearn.random_projection模块用于降低数据的维数,将对此进行解释-
Example
例
import numpy as np
from sklearn import random_projection
rannge = np.random.RandomState(0)
X = range.rand(10,2000)
X = np.array(X, dtype = 'float32')
X.dtype
Transformer_data = random_projection.GaussianRandomProjection()
X_new = transformer.fit_transform(X)
X_new.dtype
Output
输出量
dtype('float32')
dtype('float64')
In the above example, we can see that X is float32 which is cast to float64 by fit_transform(X).
在上面的示例中,我们可以看到X是float32 ,它由fit_transform(X)强制转换为float64 。
改装和更新参数 (Refitting & Updating Parameters)
Hyper-parameters of an estimator can be updated and refitted after it has been constructed via the set_params() method. Let’s see the following example to understand it −
通过set_params()方法构造估算器的超参数后,可以对其进行更新和调整。 让我们看下面的例子来理解它-
Example
例
import numpy as np
from sklearn.datasets import load_iris
from sklearn.svm import SVC
X, y = load_iris(return_X_y = True)
clf = SVC()
clf.set_params(kernel = 'linear').fit(X, y)
clf.predict(X[:5])
Output
输出量
array([0, 0, 0, 0, 0])
Once the estimator has been constructed, above code will change the default kernel rbf to linear via SVC.set_params().
一旦估计已经构造,上面的代码将更改默认内核RBF到线性经由SVC.set_params()。
Now, the following code will change back the kernel to rbf to refit the estimator and to make a second prediction.
现在,以下代码将把内核改回rbf,以重新拟合估计器并进行第二次预测。
Example
例
clf.set_params(kernel = 'rbf', gamma = 'scale').fit(X, y)
clf.predict(X[:5])
Output
输出量
array([0, 0, 0, 0, 0])
完整的代码 (Complete code)
The following is the complete executable program −
以下是完整的可执行程序-
import numpy as np
from sklearn.datasets import load_iris
from sklearn.svm import SVC
X, y = load_iris(return_X_y = True)
clf = SVC()
clf.set_params(kernel = 'linear').fit(X, y)
clf.predict(X[:5])
clf.set_params(kernel = 'rbf', gamma = 'scale').fit(X, y)
clf.predict(X[:5])
多类别和多标签拟合 (Multiclass & Multilabel fitting)
In case of multiclass fitting, both learning and the prediction tasks are dependent on the format of the target data fit upon. The module used is sklearn.multiclass. Check the example below, where multiclass classifier is fit on a 1d array.
在进行多类拟合的情况下,学习任务和预测任务都取决于适合的目标数据的格式。 使用的模块是sklearn.multiclass 。 检查下面的示例,其中多类分类器适合一维数组。
Example
例
from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import LabelBinarizer
X = [[1, 2], [3, 4], [4, 5], [5, 2], [1, 1]]
y = [0, 0, 1, 1, 2]
classif = OneVsRestClassifier(estimator = SVC(gamma = 'scale',random_state = 0))
classif.fit(X, y).predict(X)
Output
输出量
array([0, 0, 1, 1, 2])
In the above example, classifier is fit on one dimensional array of multiclass labels and the predict() method hence provides corresponding multiclass prediction. But on the other hand, it is also possible to fit upon a two-dimensional array of binary label indicators as follows −
在上面的示例中,分类器适合多类标签的一维数组,并且predict()方法因此提供了相应的多类预测。 但另一方面,也可以将二进制标签指示符的二维数组拟合如下:
Example
例
from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import LabelBinarizer
X = [[1, 2], [3, 4], [4, 5], [5, 2], [1, 1]]
y = LabelBinarizer().fit_transform(y)
classif.fit(X, y).predict(X)
Output
输出量
array(
[
[0, 0, 0],
[0, 0, 0],
[0, 1, 0],
[0, 1, 0],
[0, 0, 0]
]
)
Similarly, in case of multilabel fitting, an instance can be assigned multiple labels as follows −
类似地,在多标签拟合的情况下,可以为一个实例分配多个标签,如下所示:
Example
例
from sklearn.preprocessing import MultiLabelBinarizer
y = [[0, 1], [0, 2], [1, 3], [0, 2, 3], [2, 4]]
y = MultiLabelBinarizer().fit_transform(y)
classif.fit(X, y).predict(X)
Output
输出量
array(
[
[1, 0, 1, 0, 0],
[1, 0, 1, 0, 0],
[1, 0, 1, 1, 0],
[1, 0, 1, 1, 0],
[1, 0, 1, 0, 0]
]
)
In the above example, sklearn.MultiLabelBinarizer is used to binarize the two dimensional array of multilabels to fit upon. That’s why predict() function gives a 2d array as output with multiple labels for each instance.
在上面的示例中,使用sklearn.MultiLabelBinarizer将适合的多标签二维数组二值化。 因此,predict()函数将二维数组作为输出,每个实例带有多个标签。
Scikit Learn-线性建模 (Scikit Learn - Linear Modeling)
This chapter will help you in learning about the linear modeling in Scikit-Learn. Let us begin by understanding what is linear regression in Sklearn.
本章将帮助您学习Scikit-Learn中的线性建模。 让我们首先了解什么是Sklearn中的线性回归。
The following table lists out various linear models provided by Scikit-Learn −
下表列出了Scikit-Learn提供的各种线性模型-
| Sr.No | Model & Description |
|---|---|
| 1 | Linear Regression It is one of the best statistical models that studies the relationship between a dependent variable (Y) with a given set of independent variables (X). |
| 2 | Logistic Regression Logistic regression, despite its name, is a classification algorithm rather than regression algorithm. Based on a given set of independent variables, it is used to estimate discrete value (0 or 1, yes/no, true/false). |
| 3 | Ridge Regression Ridge regression or Tikhonov regularization is the regularization technique that performs L2 regularization. It modifies the loss function by adding the penalty (shrinkage quantity) equivalent to the square of the magnitude of coefficients. |
| 4 | Bayesian Ridge Regression Bayesian regression allows a natural mechanism to survive insufficient data or poorly distributed data by formulating linear regression using probability distributors rather than point estimates. |
| 5 | LASSO LASSO is the regularisation technique that performs L1 regularisation. It modifies the loss function by adding the penalty (shrinkage quantity) equivalent to the summation of the absolute value of coefficients. |
| 6 | Multi-task LASSO It allows to fit multiple regression problems jointly enforcing the selected features to be same for all the regression problems, also called tasks. Sklearn provides a linear model named MultiTaskLasso, trained with a mixed L1, L2-norm for regularisation, which estimates sparse coefficients for multiple regression problems jointly. |
| 7 | Elastic-Net The Elastic-Net is a regularized regression method that linearly combines both penalties i.e. L1 and L2 of the Lasso and Ridge regression methods. It is useful when there are multiple correlated features. |
| 8 | Multi-task Elastic-Net It is an Elastic-Net model that allows to fit multiple regression problems jointly enforcing the selected features to be same for all the regression problems, also called tasks |
| 序号 | 型号说明 |
|---|---|
| 1个 | 线性回归 它是研究因变量(Y)与一组给定自变量(X)之间的关系的最佳统计模型之一。 |
| 2 | 逻辑回归 逻辑回归尽管有其名称,但它是一种分类算法,而不是回归算法。 基于给定的一组独立变量,它可用于估计离散值(0或1,是/否,是/否)。 |
| 3 | 岭回归 Ridge回归或Tikhonov正则化是执行L2正则化的正则化技术。 它通过添加等于系数幅度平方的罚金(收缩量)来修改损耗函数。 |
| 4 | 贝叶斯岭回归 贝叶斯回归允许自然机制通过使用概率分布而不是点估计来制定线性回归来生存数据不足或分布不佳的数据。 |
| 5 | 套索 LASSO是执行L1正则化的正则化技术。 通过添加等于系数绝对值之和的损失(收缩量)来修改损失函数。 |
| 6 | 多任务LASSO 它允许对多个回归问题进行拟合,从而共同针对所有回归问题(也称为任务)强制使所选要素相同。 Sklearn提供了一个名为MultiTaskLasso的线性模型,使用混合的L1,L2范数进行正则化训练,该模型可以联合估计多个回归问题的稀疏系数。 |
| 7 | 弹性网 Elastic-Net是一种正则化回归方法,它线性地结合了套索和里奇回归方法中的两个惩罚,即L1和L2。 有多个相关功能时,此功能很有用。 |
| 8 | 多任务弹性网 它是一个Elastic-Net模型,允许同时拟合多个回归问题,从而使所有回归问题(也称为任务)的选定特征相同 |
Scikit Learn-扩展线性建模 (Scikit Learn - Extended Linear Modeling)
This chapter focusses on the polynomial features and pipelining tools in Sklearn.
本章重点介绍Sklearn中的多项式特征和流水线工具。
多项式特征介绍 (Introduction to Polynomial Features)
Linear models trained on non-linear functions of data generally maintains the fast performance of linear methods. It also allows them to fit a much wider range of data. That’s the reason in machine learning such linear models, that are trained on nonlinear functions, are used.
经过数据非线性函数训练的线性模型通常可以保持线性方法的快速性能。 它还允许他们适应更大范围的数据。 这就是在机器学习中使用此类经过非线性函数训练的线性模型的原因。
One such example is that a simple linear regression can be extended by constructing polynomial features from the coefficients.
一个这样的例子是,可以通过从系数构造多项式特征来扩展简单的线性回归。
Mathematically, suppose we have standard linear regression model then for 2-D data it would look like this −
$$Y=W_{0}+W_{1}X_{1}+W_{2}X_{2}$$数学上,假设我们有标准的线性回归模型,那么对于二维数据,它看起来像这样-
$$ Y = W_ {0} + W_ {1} X_ {1} + W_ {2} X_ {2} $$Now, we can combine the features in second-order polynomials and our model will look like as follows −
$$Y=W_{0}+W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{1}X_{2}+W_{4}X_1^2+W_{5}X_2^2$$现在,我们可以将特征组合到二阶多项式中,我们的模型如下所示:
$$ Y = W_ {0} + W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {1} X_ {2} + W_ {4} X_1 ^ 2 + W_ { 5} X_2 ^ 2 $$The above is still a linear model. Here, we saw that the resulting polynomial regression is in the same class of linear models and can be solved similarly.
以上仍然是线性模型。 在这里,我们看到了所得的多项式回归属于同一类线性模型,并且可以类似地求解。
To do so, scikit-learn provides a module named PolynomialFeatures. This module transforms an input data matrix into a new data matrix of given degree.
为此,scikit-learn提供了一个名为PolynomialFeatures的模块。 该模块将输入数据矩阵转换为给定程度的新数据矩阵。
参量 (Parameters)
Followings table consist the parameters used by PolynomialFeatures module
下表包含PolynomialFeatures模块使用的参数
| Sr.No | Parameter & Description |
|---|---|
| 1 | degree − integer, default = 2 It represents the degree of the polynomial features. |
| 2 | interaction_only − Boolean, default = false By default, it is false but if set as true, the features that are products of most degree distinct input features, are produced. Such features are called interaction features. |
| 3 | include_bias − Boolean, default = true It includes a bias column i.e. the feature in which all polynomials powers are zero. |
| 4 | order − str in {‘C’, ‘F’}, default = ‘C’ This parameter represents the order of output array in the dense case. ‘F’ order means faster to compute but on the other hand, it may slow down subsequent estimators. |
| 序号 | 参数及说明 |
|---|---|
| 1个 | 度 -整数,默认= 2 它代表多项式特征的程度。 |
| 2 | interact_only-布尔值,默认= false 默认情况下,它为false,但如果设置为true,则会生成大多数度数不同的输入要素的乘积。 这些功能称为交互功能。 |
| 3 | include_bias-布尔值,默认= true 它包括一个偏差列,即所有多项式幂均为零的特征。 |
| 4 | 顺序 -str in {'C','F'},默认='C' 此参数表示密集情况下输出数组的顺序。 “ F”阶意味着更快的计算,但另一方面,它可能会减慢后续的估计量。 |
属性 (Attributes)
Followings table consist the attributes used by PolynomialFeatures module
跟随表包含PolynomialFeatures模块使用的属性
| Sr.No | Attributes & Description |
|---|---|
| 1 | powers_ − array, shape (n_output_features, n_input_features) It shows powers_ [i,j] is the exponent of the jth input in the ith output. |
| 2 | n_input_features _ − int As name suggests, it gives the total number of input features. |
| 3 | n_output_features _ − int As name suggests, it gives the total number of polynomial output features. |
| 序号 | 属性和说明 |
|---|---|
| 1个 | powers_-数组,形状(n_output_features,n_input_features) 它显示powers_ [i,j]是第i个输出中第j个输入的指数。 |
| 2 | n_input_features _ − int 顾名思义,它给出了输入功能的总数。 |
| 3 | n_output_features _ − int 顾名思义,它给出了多项式输出特征的总数。 |
实施实例 (Implementation Example)
Following Python script uses PolynomialFeatures transformer to transform array of 8 into shape (4,2) −
以下Python脚本使用PolynomialFeatures转换器将8的数组转换为形状(4,2)-
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
Y = np.arange(8).reshape(4, 2)
poly = PolynomialFeatures(degree=2)
poly.fit_transform(Y)
输出量 (Output)
array(
[
[ 1., 0., 1., 0., 0., 1.],
[ 1., 2., 3., 4., 6., 9.],
[ 1., 4., 5., 16., 20., 25.],
[ 1., 6., 7., 36., 42., 49.]
]
)
使用管道工具精简 (Streamlining using Pipeline tools)
The above sort of preprocessing i.e. transforming an input data matrix into a new data matrix of a given degree, can be streamlined with the Pipeline tools, which are basically used to chain multiple estimators into one.
可以使用流水线工具简化上述类型的预处理,即将输入数据矩阵转换为给定程度的新数据矩阵,该工具基本上用于将多个估计量链接为一个。
例 (Example)
The below python scripts using Scikit-learn’s Pipeline tools to streamline the preprocessing (will fit to an order-3 polynomial data).
下面的python脚本使用Scikit-learn的Pipeline工具简化了预处理(将适合3阶多项式数据)。
#First, import the necessary packages.
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
import numpy as np
#Next, create an object of Pipeline tool
Stream_model = Pipeline([('poly', PolynomialFeatures(degree=3)), ('linear', LinearRegression(fit_intercept=False))])
#Provide the size of array and order of polynomial data to fit the model.
x = np.arange(5)
y = 3 - 2 * x + x ** 2 - x ** 3
Stream_model = model.fit(x[:, np.newaxis], y)
#Calculate the input polynomial coefficients.
Stream_model.named_steps['linear'].coef_
输出量 (Output)
array([ 3., -2., 1., -1.])
The above output shows that the linear model trained on polynomial features is able to recover the exact input polynomial coefficients.
上面的输出表明,在多项式特征上训练的线性模型能够恢复精确的输入多项式系数。
Scikit学习-随机梯度下降 (Scikit Learn - Stochastic Gradient Descent)
Here, we will learn about an optimization algorithm in Sklearn, termed as Stochastic Gradient Descent (SGD).
在这里,我们将学习Sklearn中的优化算法,称为随机梯度下降(SGD)。
Stochastic Gradient Descent (SGD) is a simple yet efficient optimization algorithm used to find the values of parameters/coefficients of functions that minimize a cost function. In other words, it is used for discriminative learning of linear classifiers under convex loss functions such as SVM and Logistic regression. It has been successfully applied to large-scale datasets because the update to the coefficients is performed for each training instance, rather than at the end of instances.
随机梯度下降(SGD)是一种简单而有效的优化算法,用于查找使成本函数最小化的函数参数/系数值。 换句话说,它用于凸损失函数(例如SVM和Logistic回归)下的线性分类器的判别学习。 它已成功应用于大型数据集,因为是针对每个训练实例(而不是在实例结束时)执行系数更新。
SGD分类器 (SGD Classifier)
Stochastic Gradient Descent (SGD) classifier basically implements a plain SGD learning routine supporting various loss functions and penalties for classification. Scikit-learn provides SGDClassifier module to implement SGD classification.
随机梯度下降(SGD)分类器基本上实现了简单的SGD学习例程,该例程支持各种损失函数和分类惩罚。 Scikit-learn提供了SGDClassifier模块来实现SGD分类。
参量 (Parameters)
Followings table consist the parameters used by SGDClassifier module −
下表包含SGDClassifier模块使用的参数-
| Sr.No | Parameter & Description |
|---|---|
| 1 | loss − str, default = ‘hinge’ It represents the loss function to be used while implementing. The default value is ‘hinge’ which will give us a linear SVM. The other options which can be used are −
|
| 2 | penalty − str, ‘none’, ‘l2’, ‘l1’, ‘elasticnet’ It is the regularization term used in the model. By default, it is L2. We can use L1 or ‘elasticnet; as well but both might bring sparsity to the model, hence not achievable with L2. |
| 3 | alpha − float, default = 0.0001 Alpha, the constant that multiplies the regularization term, is the tuning parameter that decides how much we want to penalize the model. The default value is 0.0001. |
| 4 | l1_ratio − float, default = 0.15 This is called the ElasticNet mixing parameter. Its range is 0 < = l1_ratio < = 1. If l1_ratio = 1, the penalty would be L1 penalty. If l1_ratio = 0, the penalty would be an L2 penalty. |
| 5 | fit_intercept − Boolean, Default=True This parameter specifies that a constant (bias or intercept) should be added to the decision function. No intercept will be used in calculation and data will be assumed already centered, if it will set to false. |
| 6 | tol − float or none, optional, default = 1.e-3 This parameter represents the stopping criterion for iterations. Its default value is False but if set to None, the iterations will stop when loss > best_loss - tol for n_iter_no_changesuccessive epochs. |
| 7 | shuffle − Boolean, optional, default = True This parameter represents that whether we want our training data to be shuffled after each epoch or not. |
| 8 | verbose − integer, default = 0 It represents the verbosity level. Its default value is 0. |
| 9 | epsilon − float, default = 0.1 This parameter specifies the width of the insensitive region. If loss = ‘epsilon-insensitive’, any difference, between current prediction and the correct label, less than the threshold would be ignored. |
| 10 | max_iter − int, optional, default = 1000 As name suggest, it represents the maximum number of passes over the epochs i.e. training data. |
| 11 | warm_start − bool, optional, default = false With this parameter set to True, we can reuse the solution of the previous call to fit as initialization. If we choose default i.e. false, it will erase the previous solution. |
| 12 | random_state − int, RandomState instance or None, optional, default = none This parameter represents the seed of the pseudo random number generated which is used while shuffling the data. Followings are the options.
|
| 13 | n_jobs − int or none, optional, Default = None It represents the number of CPUs to be used in OVA (One Versus All) computation, for multi-class problems. The default value is none which means 1. |
| 14 | learning_rate − string, optional, default = ‘optimal’
|
| 15 | eta0 − double, default = 0.0 It represents the initial learning rate for above mentioned learning rate options i.e. ‘constant’, ‘invscalling’, or ‘adaptive’. |
| 16 | power_t − idouble, default =0.5 It is the exponent for ‘incscalling’ learning rate. |
| 17 | early_stopping − bool, default = False This parameter represents the use of early stopping to terminate training when validation score is not improving. Its default value is false but when set to true, it automatically set aside a stratified fraction of training data as validation and stop training when validation score is not improving. |
| 18 | validation_fraction − float, default = 0.1 It is only used when early_stopping is true. It represents the proportion of training data to set asides as validation set for early termination of training data.. |
| 19 | n_iter_no_change − int, default=5 It represents the number of iteration with no improvement should algorithm run before early stopping. |
| 20 | classs_weight − dict, {class_label: weight} or “balanced”, or None, optional This parameter represents the weights associated with classes. If not provided, the classes are supposed to have weight 1. |
| 20 | warm_start − bool, optional, default = false With this parameter set to True, we can reuse the solution of the previous call to fit as initialization. If we choose default i.e. false, it will erase the previous solution. |
| 21 | average − iBoolean or int, optional, default = false It represents the number of CPUs to be used in OVA (One Versus All) computation, for multi-class problems. The default value is none which means 1. |
| 序号 | 参数及说明 |
|---|---|
| 1个 | 损失 -str,默认='铰链' 它表示实现时要使用的损失函数。 默认值为“ hinge”,这将为我们提供线性SVM。 可以使用的其他选项是-
|
| 2 | 惩罚 -str,'none','l2','l1','elasticnet' 它是模型中使用的正则化术语。 默认情况下为L2。 我们可以使用L1或'elasticnet; 同样,但是两者都可能给模型带来稀疏性,因此L2无法实现。 |
| 3 | alpha-浮点数,默认= 0.0001 Alpha(乘以正则项的常数)是调整参数,它决定了我们要对模型进行多少惩罚。 默认值为0.0001。 |
| 4 | l1_ratio-浮点数,默认= 0.15 这称为ElasticNet混合参数。 其范围为0 <= l1_ratio <=1。如果l1_ratio = 1,则惩罚为L1惩罚。 如果l1_ratio = 0,则惩罚为L2惩罚。 |
| 5 | fit_intercept-布尔值,默认为True 此参数指定应将常量(偏差或截距)添加到决策函数。 如果将其设置为false,则不会在计算中使用截距,并且将假定数据已居中。 |
| 6 | tol-浮动或无,可选,默认= 1.e-3 此参数表示迭代的停止标准。 它的默认值为False,但如果设置为None,则当n 损失 > best_loss-连续n_iter_no_change个时期的tol时,迭代将停止。 |
| 7 | shuffle-布尔值,可选,默认= True 此参数表示我们是否希望在每个时期之后对训练数据进行混洗。 |
| 8 | 详细 -整数,默认= 0 它代表了详细程度。 默认值为0。 |
| 9 | epsilon-浮动,默认= 0.1 此参数指定不敏感区域的宽度。 如果损失=“对ε不敏感”,则当前预测与正确标签之间的任何差异(小于阈值)将被忽略。 |
| 10 | max_iter -int,可选,默认= 1000 顾名思义,它代表历时的最大通过次数,即训练数据。 |
| 11 | warm_start -bool,可选,默认= false 通过将此参数设置为True,我们可以重用上一个调用的解决方案以适合初始化。 如果我们选择默认值,即false,它将删除先前的解决方案。 |
| 12 | random_state -int,RandomState实例或无,可选,默认=无 此参数表示生成的伪随机数的种子,在对数据进行混洗时会使用该种子。 以下是选项。
|
| 13 | n_jobs-整数或无,可选,默认=无 它表示用于多类问题的OVA(一个对所有)计算中使用的CPU数量。 默认值为none,表示1。 |
| 14 | learning_rate-字符串,可选,默认='最优'
|
| 15 | eta0-两倍,默认= 0.0 它代表上述学习率选项(即“恒定”,“渐进”或“自适应”)的初始学习率。 |
| 16 | power_t -idouble,默认= 0.5 它是“增加”学习率的指数。 |
| 17 | early_stopping − bool,默认= False 此参数表示当验证分数没有提高时,使用早期停止来终止训练。 它的默认值是false,但是当设置为true时,它会自动将训练数据的分层部分留作验证,并在验证得分没有提高时停止训练。 |
| 18 | validation_fraction-浮点数,默认= 0.1 仅当early_stopping为true时使用。 它表示将训练数据设置为辅助参数以尽早终止训练数据的比例。 |
| 19 | n_iter_no_change-整数,默认= 5 它表示算法的迭代次数,如果算法在尽早停止之前仍未运行,则不会有所改善。 |
| 20 | classs_weight -dict,{class_label:weight}或“ balanced”,或者“无”,可选 此参数表示与类关联的权重。 如果未提供,则该类的权重应为1。 |
| 20 | warm_start -bool,可选,默认= false 通过将此参数设置为True,我们可以重用上一个调用的解决方案以适合初始化。 如果我们选择默认值,即false,它将删除先前的解决方案。 |
| 21 | 平均值 -iBoolean或int,可选,默认= false 它表示用于多类问题的OVA(一个对所有)计算中使用的CPU数量。 默认值为none,表示1。 |
属性 (Attributes)
Following table consist the attributes used by SGDClassifier module −
下表包含SGDClassifier模块使用的属性-
| Sr.No | Attributes & Description |
|---|---|
| 1 | coef_ − array, shape (1, n_features) if n_classes==2, else (n_classes, n_features) This attribute provides the weight assigned to the features. |
| 2 | intercept_ − array, shape (1,) if n_classes==2, else (n_classes,) It represents the independent term in decision function. |
| 3 | n_iter_ − int It gives the number of iterations to reach the stopping criterion. |
| 序号 | 属性和说明 |
|---|---|
| 1个 | coef_-数组,如果n_classes == 2,则形状为(1,n_features),否则为(n_classes,n_features) 此属性提供分配给要素的权重。 |
| 2 | intercept_ -阵列的形状(1)如果n_classes == 2,否则(n_classes,) 它代表决策功能中的独立项。 |
| 3 | n_iter_-整数 它给出了达到停止标准的迭代次数。 |
Implementation Example
实施实例
Like other classifiers, Stochastic Gradient Descent (SGD) has to be fitted with following two arrays −
像其他分类器一样,随机梯度下降(SGD)必须配备以下两个数组-
An array X holding the training samples. It is of size [n_samples, n_features].
存放训练样本的数组X。 它的大小为[n_samples,n_features]。
An array Y holding the target values i.e. class labels for the training samples. It is of size [n_samples].
保存目标值的数组Y,即训练样本的类别标签。 它的大小为[n_samples]。
Example
例
Following Python script uses SGDClassifier linear model −
以下Python脚本使用SGDClassifier线性模型-
import numpy as np
from sklearn import linear_model
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
Y = np.array([1, 1, 2, 2])
SGDClf = linear_model.SGDClassifier(max_iter = 1000, tol=1e-3,penalty = "elasticnet")
SGDClf.fit(X, Y)
Output
输出量
SGDClassifier(
alpha = 0.0001, average = False, class_weight = None,
early_stopping = False, epsilon = 0.1, eta0 = 0.0, fit_intercept = True,
l1_ratio = 0.15, learning_rate = 'optimal', loss = 'hinge', max_iter = 1000,
n_iter = None, n_iter_no_change = 5, n_jobs = None, penalty = 'elasticnet',
power_t = 0.5, random_state = None, shuffle = True, tol = 0.001,
validation_fraction = 0.1, verbose = 0, warm_start = False
)
Example
例
Now, once fitted, the model can predict new values as follows −
现在,一旦拟合,模型可以预测新值,如下所示:
SGDClf.predict([[2.,2.]])
Output
输出量
array([2])
Example
例
For the above example, we can get the weight vector with the help of following python script −
对于上面的示例,我们可以借助以下python脚本获取权重向量-
SGDClf.coef_
Output
输出量
array([[19.54811198, 9.77200712]])
Example
例
Similarly, we can get the value of intercept with the help of following python script −
同样,我们可以在以下python脚本的帮助下获取拦截的值-
SGDClf.intercept_
Output
输出量
array([10.])
Example
例
We can get the signed distance to the hyperplane by using SGDClassifier.decision_function as used in the following python script −
通过使用以下python脚本中使用的SGDClassifier.decision_function ,可以获取到超平面的有符号距离-
SGDClf.decision_function([[2., 2.]])
Output
输出量
array([68.6402382])
SGD回归器 (SGD Regressor)
Stochastic Gradient Descent (SGD) regressor basically implements a plain SGD learning routine supporting various loss functions and penalties to fit linear regression models. Scikit-learn provides SGDRegressor module to implement SGD regression.
随机梯度下降(SGD)回归器基本上实现了简单的SGD学习例程,该例程支持各种损失函数和惩罚以适应线性回归模型。 Scikit-learn提供了SGDRegressor模块来实现SGD回归。
参量 (Parameters)
Parameters used by SGDRegressor are almost same as that were used in SGDClassifier module. The difference lies in ‘loss’ parameter. For SGDRegressor modules’ loss parameter the positives values are as follows −
SGDRegressor使用的参数与SGDClassifier模块中使用的参数几乎相同。 区别在于“损失”参数。 对于SGDRegressor模块的loss参数,正值如下所示-
squared_loss − It refers to the ordinary least squares fit.
squared_loss-它是指普通的最小二乘拟合。
huber: SGDRegressor − correct the outliers by switching from squared to linear loss past a distance of epsilon. The work of ‘huber’ is to modify ‘squared_loss’ so that algorithm focus less on correcting outliers.
Huber:SGDRegressor-通过将平方损失转换为线性损失超过ε距离来校正异常值。 “休伯”的工作是修改“ squared_loss”,以使算法较少关注校正异常值。
epsilon_insensitive − Actually, it ignores the errors less than epsilon.
epsilon_insensitive-实际上,它忽略小于epsilon的错误。
squared_epsilon_insensitive − It is same as epsilon_insensitive. The only difference is that it becomes squared loss past a tolerance of epsilon.
squared_epsilon_insensitive-与epsilon_insensitive相同。 唯一的区别是,它变成超过ε容差的平方损耗。
Another difference is that the parameter named ‘power_t’ has the default value of 0.25 rather than 0.5 as in SGDClassifier. Furthermore, it doesn’t have ‘class_weight’ and ‘n_jobs’ parameters.
另一个区别是名为'power_t'的参数的默认值为0.25,而不是SGDClassifier中的 0.5。 此外,它没有'class_weight'和'n_jobs'参数。
属性 (Attributes)
Attributes of SGDRegressor are also same as that were of SGDClassifier module. Rather it has three extra attributes as follows −
SGDRegressor的属性也与SGDClassifier模块的属性相同。 相反,它具有三个额外的属性,如下所示:
average_coef_ − array, shape(n_features,)
average_coef_ −数组,形状(n_features,)
As name suggest, it provides the average weights assigned to the features.
顾名思义,它提供分配给功能的平均权重。
average_intercept_ − array, shape(1,)
average_intercept_-数组,shape(1,)
As name suggest, it provides the averaged intercept term.
顾名思义,它提供了平均截距项。
t_ − int
t_-整数
It provides the number of weight updates performed during the training phase.
它提供了在训练阶段执行的体重更新次数。
Note − the attributes average_coef_ and average_intercept_ will work after enabling parameter ‘average’ to True.
注意 -在将参数“ average”启用为True之后,属性average_coef_和average_intercept_将起作用。
Implementation Example
实施实例
Following Python script uses SGDRegressor linear model −
以下Python脚本使用SGDRegressor线性模型-
import numpy as np
from sklearn import linear_model
n_samples, n_features = 10, 5
rng = np.random.RandomState(0)
y = rng.randn(n_samples)
X = rng.randn(n_samples, n_features)
SGDReg =linear_model.SGDRegressor(
max_iter = 1000,penalty = "elasticnet",loss = 'huber',tol = 1e-3, average = True
)
SGDReg.fit(X, y)
Output
输出量
SGDRegressor(
alpha = 0.0001, average = True, early_stopping = False, epsilon = 0.1,
eta0 = 0.01, fit_intercept = True, l1_ratio = 0.15,
learning_rate = 'invscaling', loss = 'huber', max_iter = 1000,
n_iter = None, n_iter_no_change = 5, penalty = 'elasticnet', power_t = 0.25,
random_state = None, shuffle = True, tol = 0.001, validation_fraction = 0.1,
verbose = 0, warm_start = False
)
Example
例
Now, once fitted, we can get the weight vector with the help of following python script −
现在,一旦拟合,我们就可以在以下python脚本的帮助下获得权重向量-
SGDReg.coef_
Output
输出量
array([-0.00423314, 0.00362922, -0.00380136, 0.00585455, 0.00396787])
Example
例
Similarly, we can get the value of intercept with the help of following python script −
同样,我们可以在以下python脚本的帮助下获取拦截的值-
SGReg.intercept_
Output
输出量
SGReg.intercept_
Example
例
We can get the number of weight updates during training phase with the help of the following python script −
我们可以借助以下python脚本获取训练阶段体重更新的次数-
SGDReg.t_
Output
输出量
61.0
SGD的优点和缺点 (Pros and Cons of SGD)
Following the pros of SGD −
遵循SGD的优点-
Stochastic Gradient Descent (SGD) is very efficient.
随机梯度下降(SGD)非常有效。
It is very easy to implement as there are lots of opportunities for code tuning.
这很容易实现,因为有很多代码调优的机会。
Following the cons of SGD −
遵循SGD的缺点-
Stochastic Gradient Descent (SGD) requires several hyperparameters like regularization parameters.
随机梯度下降(SGD)需要一些超参数,例如正则化参数。
It is sensitive to feature scaling.
它对特征缩放很敏感。
Scikit Learn-支持向量机 (Scikit Learn - Support Vector Machines)
This chapter deals with a machine learning method termed as Support Vector Machines (SVMs).
本章介绍了一种称为支持向量机(SVM)的机器学习方法。
介绍 (Introduction)
Support vector machines (SVMs) are powerful yet flexible supervised machine learning methods used for classification, regression, and, outliers’ detection. SVMs are very efficient in high dimensional spaces and generally are used in classification problems. SVMs are popular and memory efficient because they use a subset of training points in the decision function.
支持向量机(SVM)是强大而灵活的监督型机器学习方法,用于分类,回归和离群值检测。 SVM在高维空间中非常有效,通常用于分类问题。 SVM受欢迎且具有存储效率,因为它们在决策函数中使用训练点的子集。
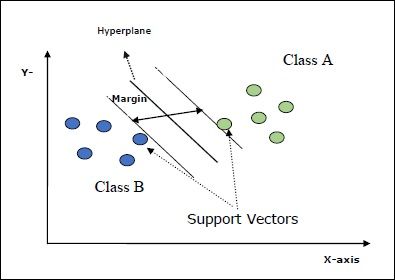
The main goal of SVMs is to divide the datasets into number of classes in order to find a maximum marginal hyperplane (MMH) which can be done in the following two steps −
SVM的主要目标是将数据集分为几类,以找到最大的边际超平面(MMH) ,可以在以下两个步骤中完成-
Support Vector Machines will first generate hyperplanes iteratively that separates the classes in the best way.
支持向量机将首先以迭代方式生成超平面,从而以最佳方式分隔类。
After that it will choose the hyperplane that segregate the classes correctly.
之后,它将选择正确隔离类的超平面。
Some important concepts in SVM are as follows −
SVM中的一些重要概念如下-
Support Vectors − They may be defined as the datapoints which are closest to the hyperplane. Support vectors help in deciding the separating line.
支持向量 -它们可以定义为最接近超平面的数据点。 支持向量有助于确定分隔线。
Hyperplane − The decision plane or space that divides set of objects having different classes.
超平面 -划分具有不同类别的对象集的决策平面或空间。
Margin − The gap between two lines on the closet data points of different classes is called margin.
裕度 -不同类别的壁橱数据点上的两条线之间的间隙称为裕度。
Following diagrams will give you an insight about these SVM concepts −
下图将为您提供有关这些SVM概念的见解-
SVM in Scikit-learn supports both sparse and dense sample vectors as input.
Scikit-learn中的SVM支持稀疏和密集样本矢量作为输入。
支持向量机的分类 (Classification of SVM)
Scikit-learn provides three classes namely SVC, NuSVC and LinearSVC which can perform multiclass-class classification.
Scikit-learn提供三个类,即SVC,NuSVC和LinearSVC ,它们可以执行多类分类。
SVC (SVC)
It is C-support vector classification whose implementation is based on libsvm. The module used by scikit-learn is sklearn.svm.SVC. This class handles the multiclass support according to one-vs-one scheme.
这是C支持向量分类,其实现基于libsvm 。 scikit-learn使用的模块是sklearn.svm.SVC 。 此类根据一对一方案处理多类支持。
参量 (Parameters)
Followings table consist the parameters used by sklearn.svm.SVC class −
followings表包含sklearn.svm.SVC类使用的参数-
| Sr.No | Parameter & Description |
|---|---|
| 1 | C − float, optional, default = 1.0 It is the penalty parameter of the error term. |
| 2 | kernel − string, optional, default = ‘rbf’ This parameter specifies the type of kernel to be used in the algorithm. we can choose any one among, ‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’. The default value of kernel would be ‘rbf’. |
| 3 | degree − int, optional, default = 3 It represents the degree of the ‘poly’ kernel function and will be ignored by all other kernels. |
| 4 | gamma − {‘scale’, ‘auto’} or float, It is the kernel coefficient for kernels ‘rbf’, ‘poly’ and ‘sigmoid’. |
| 5 | optinal default − = ‘scale’ If you choose default i.e. gamma = ‘scale’ then the value of gamma to be used by SVC is 1/(_∗.()). On the other hand, if gamma= ‘auto’, it uses 1/_. |
| 6 | coef0 − float, optional, Default=0.0 An independent term in kernel function which is only significant in ‘poly’ and ‘sigmoid’. |
| 7 | tol − float, optional, default = 1.e-3 This parameter represents the stopping criterion for iterations. |
| 8 | shrinking − Boolean, optional, default = True This parameter represents that whether we want to use shrinking heuristic or not. |
| 9 | verbose − Boolean, default: false It enables or disable verbose output. Its default value is false. |
| 10 | probability − boolean, optional, default = true This parameter enables or disables probability estimates. The default value is false, but it must be enabled before we call fit. |
| 11 | max_iter − int, optional, default = -1 As name suggest, it represents the maximum number of iterations within the solver. Value -1 means there is no limit on the number of iterations. |
| 12 | cache_size − float, optional This parameter will specify the size of the kernel cache. The value will be in MB(MegaBytes). |
| 13 | random_state − int, RandomState instance or None, optional, default = none This parameter represents the seed of the pseudo random number generated which is used while shuffling the data. Followings are the options −
|
| 14 | class_weight − {dict, ‘balanced’}, optional This parameter will set the parameter C of class j to _ℎ[]∗ for SVC. If we use the default option, it means all the classes are supposed to have weight one. On the other hand, if you choose class_weight:balanced, it will use the values of y to automatically adjust weights. |
| 15 | decision_function_shape − ovo’, ‘ovr’, default = ‘ovr’ This parameter will decide whether the algorithm will return ‘ovr’ (one-vs-rest) decision function of shape as all other classifiers, or the original ovo(one-vs-one) decision function of libsvm. |
| 16 | break_ties − boolean, optional, default = false True − The predict will break ties according to the confidence values of decision_function False − The predict will return the first class among the tied classes. |
| 序号 | 参数及说明 |
|---|---|
| 1个 | C −浮动,可选,默认= 1.0 它是误差项的惩罚参数。 |
| 2 | 内核 -字符串,可选,默认='rbf' 此参数指定算法中要使用的内核类型。 我们可以选择“线性”,“多边形”,“ rbf”,“ Sigmoid”,“预计算”中的任意一种。 kernel的默认值为'rbf' 。 |
| 3 | 度 -int,可选,默认= 3 它代表“多边形”内核功能的程度,并且将被所有其他内核忽略。 |
| 4 | 伽玛 -{'scale','auto'}或float, 它是内核“ rbf”,“ poly”和“ Sigmoid”的内核系数。 |
| 5 | 最佳默认值 -='scale' 如果选择默认值,即gamma ='scale',则SVC使用的gamma值为1 /(_∗.())。 另一方面,如果gamma ='auto',则使用1 /_。 |
| 6 | coef0-浮动,可选,默认值= 0.0 内核函数中的一个独立术语,仅对“ poly”和“ Sigmoid”有效。 |
| 7 | tol-浮动,可选,默认= 1.e-3 此参数表示迭代的停止标准。 |
| 8 | 收缩 -布尔值,可选,默认= True 此参数表示我们是否要使用缩减启发式。 |
| 9 | 详细 -布尔值,默认值:false 它启用或禁用详细输出。 其默认值为false。 |
| 10 | 概率 -布尔值,可选,默认= true 此参数启用或禁用概率估计。 默认值为false,但必须先启用它才能调用fit。 |
| 11 | max_iter -int,可选,默认= -1 顾名思义,它表示求解器中的最大迭代次数。 值-1表示对迭代次数没有限制。 |
| 12 | cache_size-浮点数,可选 此参数将指定内核缓存的大小。 该值将以MB(兆字节)为单位。 |
| 13 | random_state -int,RandomState实例或无,可选,默认=无 此参数表示生成的伪随机数的种子,在对数据进行混洗时会使用该种子。 以下是选项-
|
| 14 | class_weight- {dict,'balanced'},可选 对于SVC,此参数会将类别j的参数C设置为__ [[]]。 如果使用默认选项,则意味着所有类都应具有权重一。 另一方面,如果选择class_weight:balanced ,它将使用y的值自动调整权重。 |
| 15 | decision_function_shape -大毛”, 'OVR',默认值为'OVR' 该参数将决定算法是否返回像所有其他分类器一样的shape的'ovr' (One-VS- Rest )决策函数,或者是libsvm的原始ovo (One-VS-One)决策函数。 |
| 16 | break_ties-布尔值,可选,默认= false 正确 -预测将根据Decision_function的置信度值打破平局 False-预测将返回绑定类中的第一类。 |
属性 (Attributes)
Followings table consist the attributes used by sklearn.svm.SVC class −
followings表包含sklearn.svm.SVC类使用的属性-
| Sr.No | Attributes & Description |
|---|---|
| 1 | support_ − array-like, shape = [n_SV] It returns the indices of support vectors. |
| 2 | support_vectors_ − array-like, shape = [n_SV, n_features] It returns the support vectors. |
| 3 | n_support_ − array-like, dtype=int32, shape = [n_class] It represents the number of support vectors for each class. |
| 4 | dual_coef_ − array, shape = [n_class-1,n_SV] These are the coefficient of the support vectors in the decision function. |
| 5 | coef_ − array, shape = [n_class * (n_class-1)/2, n_features] This attribute, only available in case of linear kernel, provides the weight assigned to the features. |
| 6 | intercept_ − array, shape = [n_class * (n_class-1)/2] It represents the independent term (constant) in decision function. |
| 7 | fit_status_ − int The output would be 0 if it is correctly fitted. The output would be 1 if it is incorrectly fitted. |
| 8 | classes_ − array of shape = [n_classes] It gives the labels of the classes. |
| 序号 | 属性和说明 |
|---|---|
| 1个 | support_-类数组,形状= [n_SV] 它返回支持向量的索引。 |
| 2 | support_vectors_-类数组,形状= [n_SV,n_features] 它返回支持向量。 |
| 3 | n_support_-类似于数组,dtype = int32,形状= [n_class] 它代表每个类的支持向量的数量。 |
| 4 | dual_coef_ −数组,形状= [n_class-1,n_SV] 这些是决策函数中支持向量的系数。 |
| 5 | coef_ −数组,形状= [n_class *(n_class-1)/ 2,n_features] 此属性仅在线性核的情况下可用,提供分配给要素的权重。 |
| 6 | intercept_ -阵列,形状= [n_class *(n_class-1)/ 2] 它代表决策功能中的独立项(常数)。 |
| 7 | fit_status_-整数 如果正确安装,输出将为0。 如果安装不正确,输出将为1。 |
| 8 | classes_-形状数组= [n_classes] 它给出了类别的标签。 |
Implementation Example
实施实例
Like other classifiers, SVC also has to be fitted with following two arrays −
像其他分类器一样,SVC还必须配备以下两个数组-
An array X holding the training samples. It is of size [n_samples, n_features].
存放训练样本的数组X。 它的大小为[n_samples,n_features]。
An array Y holding the target values i.e. class labels for the training samples. It is of size [n_samples].
保存目标值的数组Y ,即训练样本的类别标签。 它的大小为[n_samples]。
Following Python script uses sklearn.svm.SVC class −
以下Python脚本使用sklearn.svm.SVC类-
import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import SVC
SVCClf = SVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
SVCClf.fit(X, y)
Output
输出量
SVC(C = 1.0, cache_size = 200, class_weight = None, coef0 = 0.0,
decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
max_iter = -1, probability = False, random_state = None, shrinking = False,
tol = 0.001, verbose = False)
Example
例
Now, once fitted, we can get the weight vector with the help of following python script −
现在,一旦拟合,我们就可以在以下python脚本的帮助下获得权重向量-
SVCClf.coef_
Output
输出量
array([[0.5, 0.5]])
Example
例
Similarly, we can get the value of other attributes as follows −
类似地,我们可以获取其他属性的值,如下所示:
SVCClf.predict([[-0.5,-0.8]])
Output
输出量
array([1])
Example
例
SVCClf.n_support_
Output
输出量
array([1, 1])
Example
例
SVCClf.support_vectors_
Output
输出量
array(
[
[-1., -1.],
[ 1., 1.]
]
)
Example
例
SVCClf.support_
Output
输出量
array([0, 2])
Example
例
SVCClf.intercept_
Output
输出量
array([-0.])
Example
例
SVCClf.fit_status_
Output
输出量
0
NuSVC (NuSVC)
NuSVC is Nu Support Vector Classification. It is another class provided by scikit-learn which can perform multi-class classification. It is like SVC but NuSVC accepts slightly different sets of parameters. The parameter which is different from SVC is as follows −
NuSVC是Nu支持向量分类。 它是scikit-learn提供的另一个类,可以执行多类分类。 就像SVC一样,但是NuSVC接受略有不同的参数集。 与SVC不同的参数如下-
nu − float, optional, default = 0.5
nu-浮动,可选,默认= 0.5
It represents an upper bound on the fraction of training errors and a lower bound of the fraction of support vectors. Its value should be in the interval of (o,1].
它代表训练误差分数的上限和支持向量分数的下限。 其值应在(o,1]的间隔内。
Rest of the parameters and attributes are same as of SVC.
其余参数和属性与SVC相同。
实施实例 (Implementation Example)
We can implement the same example using sklearn.svm.NuSVC class also.
我们也可以使用sklearn.svm.NuSVC类实现相同的示例。
import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import NuSVC
NuSVCClf = NuSVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
NuSVCClf.fit(X, y)
输出量 (Output)
NuSVC(cache_size = 200, class_weight = None, coef0 = 0.0,
decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
max_iter = -1, nu = 0.5, probability = False, random_state = None,
shrinking = False, tol = 0.001, verbose = False)
We can get the outputs of rest of the attributes as did in the case of SVC.
我们可以像SVC一样获得其余属性的输出。
线性SVC (LinearSVC)
It is Linear Support Vector Classification. It is similar to SVC having kernel = ‘linear’. The difference between them is that LinearSVC implemented in terms of liblinear while SVC is implemented in libsvm. That’s the reason LinearSVC has more flexibility in the choice of penalties and loss functions. It also scales better to large number of samples.
这是线性支持向量分类。 它类似于具有内核=“线性”的SVC。 它们之间的区别在于LinearSVC是根据liblinear实现的,而SVC是在libsvm中实现的。 这就是LinearSVC在罚分和损失函数选择方面具有更大灵活性的原因。 它还可以更好地扩展到大量样本。
If we talk about its parameters and attributes then it does not support ‘kernel’ because it is assumed to be linear and it also lacks some of the attributes like support_, support_vectors_, n_support_, fit_status_ and, dual_coef_.
如果我们谈论它的参数和属性,那么它就不支持“内核”,因为它被认为是线性的,并且还缺少一些属性,例如support_,support_vectors_,n_support_,fit_status_和dual_coef_ 。
However, it supports penalty and loss parameters as follows −
但是,它支持惩罚和损失参数,如下所示:
penalty − string, L1 or L2(default = ‘L2’)
惩罚-字符串,L1或L2(默认='L2')
This parameter is used to specify the norm (L1 or L2) used in penalization (regularization).
此参数用于指定惩罚(正则化)中使用的标准(L1或L2)。
loss − string, hinge, squared_hinge (default = squared_hinge)
loss-字符串,铰链,squared_hinge(默认值= squared_hinge)
It represents the loss function where ‘hinge’ is the standard SVM loss and ‘squared_hinge’ is the square of hinge loss.
它表示损耗函数,其中“铰链”是标准SVM损耗,“ squared_hinge”是铰链损耗的平方。
实施实例 (Implementation Example)
Following Python script uses sklearn.svm.LinearSVC class −
以下Python脚本使用sklearn.svm.LinearSVC类-
from sklearn.svm import LinearSVC
from sklearn.datasets import make_classification
X, y = make_classification(n_features = 4, random_state = 0)
LSVCClf = LinearSVC(dual = False, random_state = 0, penalty = 'l1',tol = 1e-5)
LSVCClf.fit(X, y)
输出量 (Output)
LinearSVC(C = 1.0, class_weight = None, dual = False, fit_intercept = True,
intercept_scaling = 1, loss = 'squared_hinge', max_iter = 1000,
multi_class = 'ovr', penalty = 'l1', random_state = 0, tol = 1e-05, verbose = 0)
例 (Example)
Now, once fitted, the model can predict new values as follows −
现在,一旦拟合,模型可以预测新值,如下所示:
LSVCClf.predict([[0,0,0,0]])
输出量 (Output)
[1]
例 (Example)
For the above example, we can get the weight vector with the help of following python script −
对于上面的示例,我们可以借助以下python脚本获取权重向量-
LSVCClf.coef_
输出量 (Output)
[[0. 0. 0.91214955 0.22630686]]
例 (Example)
Similarly, we can get the value of intercept with the help of following python script −
同样,我们可以在以下python脚本的帮助下获取拦截的值-
LSVCClf.intercept_
输出量 (Output)
[0.26860518]
支持向量机回归 (Regression with SVM)
As discussed earlier, SVM is used for both classification and regression problems. Scikit-learn’s method of Support Vector Classification (SVC) can be extended to solve regression problems as well. That extended method is called Support Vector Regression (SVR).
如前所述,SVM用于分类和回归问题。 Scikit-learn的支持向量分类(SVC)方法也可以扩展为解决回归问题。 该扩展方法称为支持向量回归(SVR)。
SVM和SVR之间的基本相似之处 (Basic similarity between SVM and SVR)
The model created by SVC depends only on a subset of training data. Why? Because the cost function for building the model doesn’t care about training data points that lie outside the margin.
SVC创建的模型仅取决于训练数据的子集。 为什么? 因为构建模型的成本函数并不关心位于边距之外的训练数据点。
Whereas, the model produced by SVR (Support Vector Regression) also only depends on a subset of the training data. Why? Because the cost function for building the model ignores any training data points close to the model prediction.
而SVR(支持向量回归)产生的模型也仅取决于训练数据的子集。 为什么? 因为用于构建模型的成本函数会忽略任何接近模型预测的训练数据点。
Scikit-learn provides three classes namely SVR, NuSVR and LinearSVR as three different implementations of SVR.
Scikit-learn提供了三个类,即SVR,NuSVR和LinearSVR,作为SVR的三种不同实现。
SVR (SVR)
It is Epsilon-support vector regression whose implementation is based on libsvm. As opposite to SVC There are two free parameters in the model namely ‘C’ and ‘epsilon’.
这是Epsilon支持的向量回归,其实现基于libsvm 。 与SVC相反,模型中有两个自由参数,即'C'和'epsilon' 。
epsilon − float, optional, default = 0.1
epsilon-浮动,可选,默认= 0.1
It represents the epsilon in the epsilon-SVR model, and specifies the epsilon-tube within which no penalty is associated in the training loss function with points predicted within a distance epsilon from the actual value.
它代表epsilon-SVR模型中的epsilon,并指定在epsilon-tube中训练损失函数中与从实际值算起的距离epsilon中预测的点无关的惩罚。
Rest of the parameters and attributes are similar as we used in SVC.
其余的参数和属性与我们在SVC中使用的相似。
实施实例 (Implementation Example)
Following Python script uses sklearn.svm.SVR class −
以下Python脚本使用sklearn.svm.SVR类-
from sklearn import svm
X = [[1, 1], [2, 2]]
y = [1, 2]
SVRReg = svm.SVR(kernel = ’linear’, gamma = ’auto’)
SVRReg.fit(X, y)
输出量 (Output)
SVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, epsilon = 0.1, gamma = 'auto',
kernel = 'linear', max_iter = -1, shrinking = True, tol = 0.001, verbose = False)
例 (Example)
Now, once fitted, we can get the weight vector with the help of following python script −
现在,一旦拟合,我们就可以在以下python脚本的帮助下获得权重向量-
SVRReg.coef_
输出量 (Output)
array([[0.4, 0.4]])
例 (Example)
Similarly, we can get the value of other attributes as follows −
类似地,我们可以获取其他属性的值,如下所示:
SVRReg.predict([[1,1]])
输出量 (Output)
array([1.1])
Similarly, we can get the values of other attributes as well.
同样,我们也可以获取其他属性的值。
NuSVR (NuSVR)
NuSVR is Nu Support Vector Regression. It is like NuSVC, but NuSVR uses a parameter nu to control the number of support vectors. And moreover, unlike NuSVC where nu replaced C parameter, here it replaces epsilon.
NuSVR是Nu支持向量回归。 就像NuSVC一样,但是NuSVR使用参数nu来控制支持向量的数量。 而且,与NuSVC的nu替换了C参数不同,此处它替换了epsilon 。
实施实例 (Implementation Example)
Following Python script uses sklearn.svm.SVR class −
以下Python脚本使用sklearn.svm.SVR类-
from sklearn.svm import NuSVR
import numpy as np
n_samples, n_features = 20, 15
np.random.seed(0)
y = np.random.randn(n_samples)
X = np.random.randn(n_samples, n_features)
NuSVRReg = NuSVR(kernel = 'linear', gamma = 'auto',C = 1.0, nu = 0.1)^M
NuSVRReg.fit(X, y)
输出量 (Output)
NuSVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, gamma = 'auto',
kernel = 'linear', max_iter = -1, nu = 0.1, shrinking = True, tol = 0.001,
verbose = False)
例 (Example)
Now, once fitted, we can get the weight vector with the help of following python script −
现在,一旦拟合,我们就可以在以下python脚本的帮助下获得权重向量-
NuSVRReg.coef_
输出量 (Output)
array(
[
[-0.14904483, 0.04596145, 0.22605216, -0.08125403, 0.06564533,
0.01104285, 0.04068767, 0.2918337 , -0.13473211, 0.36006765,
-0.2185713 , -0.31836476, -0.03048429, 0.16102126, -0.29317051]
]
)
Similarly, we can get the value of other attributes as well.
同样,我们也可以获取其他属性的值。
线性SVR (LinearSVR)
It is Linear Support Vector Regression. It is similar to SVR having kernel = ‘linear’. The difference between them is that LinearSVR implemented in terms of liblinear, while SVC implemented in libsvm. That’s the reason LinearSVR has more flexibility in the choice of penalties and loss functions. It also scales better to large number of samples.
它是线性支持向量回归。 它类似于具有内核=“线性”的SVR。 它们之间的区别是,在LinearSVR的liblinear方面实施,而SVC在LIBSVM实现。 这就是LinearSVR在罚分和损失函数选择方面更具灵活性的原因。 它还可以更好地扩展到大量样本。
If we talk about its parameters and attributes then it does not support ‘kernel’ because it is assumed to be linear and it also lacks some of the attributes like support_, support_vectors_, n_support_, fit_status_ and, dual_coef_.
如果我们谈论它的参数和属性,那么它就不支持“内核”,因为它被认为是线性的,并且还缺少一些属性,例如support_,support_vectors_,n_support_,fit_status_和dual_coef_ 。
However, it supports ‘loss’ parameters as follows −
但是,它支持以下“损失”参数-
loss − string, optional, default = ‘epsilon_insensitive’
loss-字符串,可选,默认='epsilon_insensitive'
It represents the loss function where epsilon_insensitive loss is the L1 loss and the squared epsilon-insensitive loss is the L2 loss.
它表示损失函数,其中epsilon_insensitive损失是L1损失,平方的epsilon_insensitive损失是L2损失。
实施实例 (Implementation Example)
Following Python script uses sklearn.svm.LinearSVR class −
以下Python脚本使用sklearn.svm.LinearSVR类-
from sklearn.svm import LinearSVR
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 4, random_state = 0)
LSVRReg = LinearSVR(dual = False, random_state = 0,
loss = 'squared_epsilon_insensitive',tol = 1e-5)
LSVRReg.fit(X, y)
输出量 (Output)
LinearSVR(
C=1.0, dual=False, epsilon=0.0, fit_intercept=True,
intercept_scaling=1.0, loss='squared_epsilon_insensitive',
max_iter=1000, random_state=0, tol=1e-05, verbose=0
)
例 (Example)
Now, once fitted, the model can predict new values as follows −
现在,一旦拟合,模型可以预测新值,如下所示:
LSRReg.predict([[0,0,0,0]])
输出量 (Output)
array([-0.01041416])
例 (Example)
For the above example, we can get the weight vector with the help of following python script −
对于上面的示例,我们可以借助以下python脚本获取权重向量-
LSRReg.coef_
输出量 (Output)
array([20.47354746, 34.08619401, 67.23189022, 87.47017787])
例 (Example)
Similarly, we can get the value of intercept with the help of following python script −
同样,我们可以在以下python脚本的帮助下获取拦截的值-
LSRReg.intercept_
输出量 (Output)
array([-0.01041416])
Scikit Learn-异常检测 (Scikit Learn - Anomaly Detection)
Here, we will learn about what is anomaly detection in Sklearn and how it is used in identification of the data points.
在这里,我们将了解什么是Sklearn中的异常检测以及如何将其用于识别数据点。
Anomaly detection is a technique used to identify data points in dataset that does not fit well with the rest of the data. It has many applications in business such as fraud detection, intrusion detection, system health monitoring, surveillance, and predictive maintenance. Anomalies, which are also called outlier, can be divided into following three categories −
异常检测是一种用于识别数据集中与其他数据不太吻合的数据点的技术。 它在商业中具有许多应用程序,例如欺诈检测,入侵检测,系统运行状况监视,监视和预测性维护。 异常也称为离群值,可以分为以下三类:
Point anomalies − It occurs when an individual data instance is considered as anomalous w.r.t the rest of the data.
点异常 -当单个数据实例被认为与其余数据异常时,会发生异常。
Contextual anomalies − Such kind of anomaly is context specific. It occurs if a data instance is anomalous in a specific context.
上下文异常 -这种异常是上下文特定的。 如果数据实例在特定上下文中异常,则会发生这种情况。
Collective anomalies − It occurs when a collection of related data instances is anomalous w.r.t entire dataset rather than individual values.
集体异常 -当相关数据实例的集合相对于整个数据集而不是单个值异常时,就会发生这种情况。
方法 (Methods)
Two methods namely outlier detection and novelty detection can be used for anomaly detection. It’s necessary to see the distinction between them.
异常检测可以使用异常检测和新颖性检测这两种方法。 有必要看到它们之间的区别。
离群值检测 (Outlier detection)
The training data contains outliers that are far from the rest of the data. Such outliers are defined as observations. That’s the reason, outlier detection estimators always try to fit the region having most concentrated training data while ignoring the deviant observations. It is also known as unsupervised anomaly detection.
训练数据包含离其他数据远的异常值。 这些异常值被定义为观察值。 这就是原因,离群检测估计器总是尝试拟合训练数据最集中的区域,而忽略了异常观测值。 这也称为无监督异常检测。
新颖性检测 (Novelty detection)
It is concerned with detecting an unobserved pattern in new observations which is not included in training data. Here, the training data is not polluted by the outliers. It is also known as semi-supervised anomaly detection.
它与在训练数据中不包括的新观察中检测到未观察到的模式有关。 在这里,训练数据不受异常值的污染。 这也称为半监督异常检测。
There are set of ML tools, provided by scikit-learn, which can be used for both outlier detection as well novelty detection. These tools first implementing object learning from the data in an unsupervised by using fit () method as follows −
scikit-learn提供了一套ML工具,可用于异常检测和新颖性检测。 这些工具首先通过使用fit()方法在无监督的情况下从数据中实现对象学习-
estimator.fit(X_train)
Now, the new observations would be sorted as inliers (labeled 1) or outliers (labeled -1) by using predict() method as follows −
现在,可以通过使用predict()方法将新观察值分类为离群值(标记 为1)或离群值(标记为-1) ,如下所示:
estimator.fit(X_test)
The estimator will first compute the raw scoring function and then predict method will make use of threshold on that raw scoring function. We can access this raw scoring function with the help of score_sample method and can control the threshold by contamination parameter.
估计器将首先计算原始评分函数,然后预测方法将使用该原始评分函数的阈值。 我们可以借助score_sample方法访问此原始评分功能,并可以通过污染参数控制阈值。
We can also define decision_function method that defines outliers as negative value and inliers as non-negative value.
我们还可以定义Decision_function方法,将离群值定义为负值,将离群值定义为非负值。
estimator.decision_function(X_test)
用于异常值检测的Sklearn算法 (Sklearn algorithms for Outlier Detection)
Let us begin by understanding what an elliptic envelop is.
让我们首先了解什么是椭圆形信封。
拟合椭圆形信封 (Fitting an elliptic envelop)
This algorithm assume that regular data comes from a known distribution such as Gaussian distribution. For outlier detection, Scikit-learn provides an object named covariance.EllipticEnvelop.
该算法假定常规数据来自已知分布,例如高斯分布。 为了检测异常值,Scikit-learn提供了一个名为covariance.EllipticEnvelop的对象。
This object fits a robust covariance estimate to the data, and thus, fits an ellipse to the central data points. It ignores the points outside the central mode.
该对象将稳健的协方差估计值拟合到数据,因此将椭圆拟合到中心数据点。 它忽略中心模式之外的点。
参量 (Parameters)
Following table consist the parameters used by sklearn. covariance.EllipticEnvelop method −
下表包含sklearn使用的参数。 covariance.EllipticEnvelop方法-
| Sr.No | Parameter & Description |
|---|---|
| 1 | store_precision − Boolean, optional, default = True We can specify it if the estimated precision is stored. |
| 2 | assume_centered − Boolean, optional, default = False If we set it False, it will compute the robust location and covariance directly with the help of FastMCD algorithm. On the other hand, if set True, it will compute the support of robust location and covarian. |
| 3 | support_fraction − float in (0., 1.), optional, default = None This parameter tells the method that how much proportion of points to be included in the support of the raw MCD estimates. |
| 4 | contamination − float in (0., 1.), optional, default = 0.1 It provides the proportion of the outliers in the data set. |
| 5 | random_state − int, RandomState instance or None, optional, default = none This parameter represents the seed of the pseudo random number generated which is used while shuffling the data. Followings are the options −
|
| 序号 | 参数及说明 |
|---|---|
| 1个 | store_precision-布尔值,可选,默认= True 如果存储了估计的精度,我们可以指定它。 |
| 2 | 假定为中心 -布尔值,可选,默认= False 如果将其设置为False,它将直接在FastMCD算法的帮助下计算鲁棒的位置和协方差。 另一方面,如果设置为True,它将计算对稳健位置和协方差的支持。 |
| 3 | support_fraction-浮入(0.,1.),可选,默认= None 此参数告诉方法原始MCD估计的支持中将包含多少比例的点。 |
| 4 | 污染 -漂浮在(0.,1.)中,可选,默认= 0.1 它提供了异常值在数据集中的比例。 |
| 5 | random_state -int,RandomState实例或无,可选,默认=无 此参数表示生成的伪随机数的种子,在对数据进行混洗时会使用该种子。 以下是选项-
|
属性 (Attributes)
Following table consist the attributes used by sklearn. covariance.EllipticEnvelop method −
下表包含sklearn使用的属性。 covariance.EllipticEnvelop方法-
| Sr.No | Attributes & Description |
|---|---|
| 1 | support_ − array-like, shape(n_samples,) It represents the mask of the observations used to compute robust estimates of location and shape. |
| 2 | location_ − array-like, shape (n_features) It returns the estimated robust location. |
| 3 | covariance_ − array-like, shape (n_features, n_features) It returns the estimated robust covariance matrix. |
| 4 | precision_ − array-like, shape (n_features, n_features) It returns the estimated pseudo inverse matrix. |
| 5 | offset_ − float It is used to define the decision function from the raw scores. decision_function = score_samples -offset_ |
| 序号 | 属性和说明 |
|---|---|
| 1个 | support_-像数组一样的形状(n_samples,) 它代表用于计算位置和形状的可靠估计值的观测值的遮罩。 |
| 2 | location_-阵列状,形状(n_features) 它返回估计的稳健位置。 |
| 3 | covariance_-数组状,形状(n_features,n_features) 它返回估计的鲁棒协方差矩阵。 |
| 4 | precision_-像数组一样的形状(n_features,n_features) 它返回估计的伪逆矩阵。 |
| 5 | offset_-浮动 它用于根据原始分数定义决策函数。 决策功能=分数样本-偏移量 |
Implementation Example
实施实例
import numpy as np^M
from sklearn.covariance import EllipticEnvelope^M
true_cov = np.array([[.5, .6],[.6, .4]])
X = np.random.RandomState(0).multivariate_normal(mean = [0, 0], cov=true_cov,size=500)
cov = EllipticEnvelope(random_state = 0).fit(X)^M
# Now we can use predict method. It will return 1 for an inlier and -1 for an outlier.
cov.predict([[0, 0],[2, 2]])
Output
输出量
array([ 1, -1])
隔离林 (Isolation Forest)
In case of high-dimensional dataset, one efficient way for outlier detection is to use random forests. The scikit-learn provides ensemble.IsolationForest method that isolates the observations by randomly selecting a feature. Afterwards, it randomly selects a value between the maximum and minimum values of the selected features.
对于高维数据集,一种有效的离群值检测方法是使用随机森林。 scikit-learn提供了ensemble.IsolationForest方法,该方法通过随机选择特征来隔离观察结果。 之后,它会在所选特征的最大值和最小值之间随机选择一个值。
Here, the number of splitting needed to isolate a sample is equivalent to path length from the root node to the terminating node.
在这里,隔离样本所需的拆分次数等于从根节点到终止节点的路径长度。
参量 (Parameters)
Followings table consist the parameters used by sklearn. ensemble.IsolationForest method −
跟随表包括sklearn使用的参数。 ensemble.IsolationForest方法-
| Sr.No | Parameter & Description |
|---|---|
| 1 | n_estimators − int, optional, default = 100 It represents the number of base estimators in the ensemble. |
| 2 | max_samples − int or float, optional, default = “auto” It represents the number of samples to be drawn from X to train each base estimator. If we choose int as its value, it will draw max_samples samples. If we choose float as its value, it will draw max_samples ∗ .shape[0] samples. And, if we choose auto as its value, it will draw max_samples = min(256,n_samples). |
| 3 | support_fraction − float in (0., 1.), optional, default = None This parameter tells the method that how much proportion of points to be included in the support of the raw MCD estimates. |
| 4 | contamination − auto or float, optional, default = auto It provides the proportion of the outliers in the data set. If we set it default i.e. auto, it will determine the threshold as in the original paper. If set to float, the range of contamination will be in the range of [0,0.5]. |
| 5 | random_state − int, RandomState instance or None, optional, default = none This parameter represents the seed of the pseudo random number generated which is used while shuffling the data. Followings are the options −
|
| 6 | max_features − int or float, optional (default = 1.0) It represents the number of features to be drawn from X to train each base estimator. If we choose int as its value, it will draw max_features features. If we choose float as its value, it will draw max_features * X.shape[] samples. |
| 7 | bootstrap − Boolean, optional (default = False) Its default option is False which means the sampling would be performed without replacement. And on the other hand, if set to True, means individual trees are fit on a random subset of the training data sampled with replacement. |
| 8 | n_jobs − int or None, optional (default = None) It represents the number of jobs to be run in parallel for fit() and predict() methods both. |
| 9 | verbose − int, optional (default = 0) This parameter controls the verbosity of the tree building process. |
| 10 | warm_start − Bool, optional (default=False) If warm_start = true, we can reuse previous calls solution to fit and can add more estimators to the ensemble. But if is set to false, we need to fit a whole new forest. |
| 序号 | 参数及说明 |
|---|---|
| 1个 | n_estimators -int,可选,默认= 100 它表示集合中基本估计量的数量。 |
| 2 | max_samples -int或float,可选,默认=“ auto” 它表示要从X抽取以训练每个基本估计量的样本数。 如果我们选择int作为其值,它将绘制max_samples个样本。 如果选择float作为其值,它将绘制max_samples * .shape [0]个样本。 并且,如果我们选择auto作为其值,它将绘制max_samples = min(256,n_samples)。 |
| 3 | support_fraction-浮入(0.,1.),可选,默认= None 此参数告诉方法原始MCD估计的支持中将包含多少比例的点。 |
| 4 | 污染 -自动或浮动,可选,默认=自动 它提供了异常值在数据集中的比例。 如果我们将其设置为默认值,即自动,它将像原始纸张一样确定阈值。 如果设置为浮动,则污染范围将在[0,0.5]范围内。 |
| 5 | random_state -int,RandomState实例或无,可选,默认=无 此参数表示生成的伪随机数的种子,在对数据进行混洗时会使用该种子。 以下是选项-
|
| 6 | max_features -int或float,可选(默认= 1.0) 它表示从X绘制以训练每个基本估计量的要素数量。 如果我们选择int作为其值,它将绘制max_features特征。 如果选择float作为其值,它将绘制max_features * X.shape []样本。 |
| 7 | bootstrap-布尔值,可选(默认= False) 其默认选项为False,这意味着将执行采样而无需替换。 另一方面,如果将其设置为True,则意味着将单独的树拟合到替换采样的训练数据的随机子集上。 |
| 8 | n_jobs -int或None,可选(默认= None) 它代表fit()和predict()方法并行运行的作业数。 |
| 9 | 详细 -int,可选(默认= 0) 此参数控制树构建过程的详细程度。 |
| 10 | warm_start-布尔型,可选(默认= False) 如果warm_start = true,我们可以重用以前的调用解决方案以适应并可以向集合添加更多估计量。 但是,如果将其设置为false,则需要适应一个全新的森林。 |
属性 (Attributes)
Following table consist the attributes used by sklearn. ensemble.IsolationForest method −
下表包含sklearn使用的属性。 ensemble.IsolationForest方法-
| Sr.No | Attributes & Description |
|---|---|
| 1 | estimators_ − list of DecisionTreeClassifier Providing the collection of all fitted sub-estimators. |
| 2 | max_samples_ − integer It provides the actual number of samples used. |
| 3 | offset_ − float It is used to define the decision function from the raw scores. decision_function = score_samples -offset_ |
| 序号 | 属性和说明 |
|---|---|
| 1个 | estimators_ -DecisionTreeClassifier列表 提供所有拟合的子估计量的集合。 |
| 2 | max_samples_-整数 它提供了实际使用的样本数。 |
| 3 | offset_-浮动 它用于根据原始分数定义决策函数。 决策功能=分数样本-偏移量 |
Implementation Example
实施实例
The Python script below will use sklearn. ensemble.IsolationForest method to fit 10 trees on given data
下面的Python脚本将使用sklearn。 ensemble.IsolationForest方法可在给定数据上拟合10棵树
from sklearn.ensemble import IsolationForest
import numpy as np
X = np.array([[-1, -2], [-3, -3], [-3, -4], [0, 0], [-50, 60]])
OUTDClf = IsolationForest(n_estimators = 10)
OUTDclf.fit(X)
Output
输出量
IsolationForest(
behaviour = 'old', bootstrap = False, contamination='legacy',
max_features = 1.0, max_samples = 'auto', n_estimators = 10, n_jobs=None,
random_state = None, verbose = 0
)
局部离群因子 (Local Outlier Factor)
Local Outlier Factor (LOF) algorithm is another efficient algorithm to perform outlier detection on high dimension data. The scikit-learn provides neighbors.LocalOutlierFactor method that computes a score, called local outlier factor, reflecting the degree of anomality of the observations. The main logic of this algorithm is to detect the samples that have a substantially lower density than its neighbors. Thats why it measures the local density deviation of given data points w.r.t. their neighbors.
局部离群因子(LOF)算法是对高维数据执行离群检测的另一种有效算法。 scikit-learn提供neighbors.LocalOutlierFactor方法,该方法计算得分(称为局部异常值),以反映观测值的异常程度。 该算法的主要逻辑是检测密度远低于其邻居密度的样本。 这就是为什么它测量给定数据点及其邻居的局部密度偏差的原因。
参量 (Parameters)
Followings table consist the parameters used by sklearn. neighbors.LocalOutlierFactor method
跟随表包括sklearn使用的参数。 neighbors.LocalOutlierFactor方法
| Sr.No | Parameter & Description |
|---|---|
| 1 | n_neighbors − int, optional, default = 20 It represents the number of neighbors use by default for kneighbors query. All samples would be used if . |
| 2 | algorithm − optional Which algorithm to be used for computing nearest neighbors.
|
| 3 | leaf_size − int, optional, default = 30 The value of this parameter can affect the speed of the construction and query. It also affects the memory required to store the tree. This parameter is passed to BallTree or KdTree algorithms. |
| 4 | contamination − auto or float, optional, default = auto It provides the proportion of the outliers in the data set. If we set it default i.e. auto, it will determine the threshold as in the original paper. If set to float, the range of contamination will be in the range of [0,0.5]. |
| 5 | metric − string or callable, default It represents the metric used for distance computation. |
| 6 | P − int, optional (default = 2) It is the parameter for the Minkowski metric. P=1 is equivalent to using manhattan_distance i.e. L1, whereas P=2 is equivalent to using euclidean_distance i.e. L2. |
| 7 | novelty − Boolean, (default = False) By default, LOF algorithm is used for outlier detection but it can be used for novelty detection if we set novelty = true. |
| 8 | n_jobs − int or None, optional (default = None) It represents the number of jobs to be run in parallel for fit() and predict() methods both. |
| 序号 | 参数及说明 |
|---|---|
| 1个 | n_neighbors − int,可选,默认= 20 它表示默认情况下用于kneighbors查询的邻居数。 如果使用所有样本。 |
| 2 | 算法 -可选 用于计算最近邻居的算法。
|
| 3 | leaf_size − int,可选,默认= 30 该参数的值会影响构造和查询的速度。 它还会影响存储树所需的内存。 此参数传递给BallTree或KdTree算法。 |
| 4 | 污染 -自动或浮动,可选,默认=自动 它提供了异常值在数据集中的比例。 如果我们将其设置为默认值,即自动,它将像原始纸张一样确定阈值。 如果设置为浮动,则污染范围将在[0,0.5]范围内。 |
| 5 | 指标 -字符串或可调用,默认 它代表用于距离计算的度量。 |
| 6 | P − int,可选(默认= 2) 它是Minkowski指标的参数。 P = 1等同于使用manhattan_distance即L1,而P = 2等同于使用euclidean_distance即L2。 |
| 7 | 新颖性 -布尔值,(默认= False) 默认情况下,LOF算法用于离群值检测,但是如果我们将novellity = true设置,则可以将其用于新颖性检测。 |
| 8 | n_jobs -int或None,可选(默认= None) 它代表fit()和predict()方法并行运行的作业数。 |
属性 (Attributes)
Following table consist the attributes used by sklearn.neighbors.LocalOutlierFactor method −
下表包含sklearn.neighbors.LocalOutlierFactor方法使用的属性-
| Sr.No | Attributes & Description |
|---|---|
| 1 | negative_outlier_factor_ − numpy array, shape(n_samples,) Providing opposite LOF of the training samples. |
| 2 | n_neighbors_ − integer It provides the actual number of neighbors used for neighbors queries. |
| 3 | offset_ − float It is used to define the binary labels from the raw scores. |
| 序号 | 属性和说明 |
|---|---|
| 1个 | negative_outlier_factor_ − numpy数组,形状(n_samples,) 提供训练样本的相反LOF。 |
| 2 | n_neighbors_-整数 它提供了用于邻居查询的邻居的实际数量。 |
| 3 | offset_-浮动 它用于根据原始分数定义二进制标签。 |
Implementation Example
实施实例
The Python script given below will use sklearn.neighbors.LocalOutlierFactor method to construct NeighborsClassifier class from any array corresponding our data set
下面给出的Python脚本将使用sklearn.neighbors.LocalOutlierFactor方法从对应于我们数据集的任何数组构造NeighborsClassifier类
from sklearn.neighbors import NearestNeighbors
samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]]
LOFneigh = NearestNeighbors(n_neighbors = 1, algorithm = "ball_tree",p=1)
LOFneigh.fit(samples)
Output
输出量
NearestNeighbors(
algorithm = 'ball_tree', leaf_size = 30, metric='minkowski',
metric_params = None, n_jobs = None, n_neighbors = 1, p = 1, radius = 1.0
)
Example
例
Now, we can ask from this constructed classifier is the closet point to [0.5, 1., 1.5] by using the following python script −
现在,我们可以使用以下python脚本从此构造的分类器中询问[0.5,1.,1.5]的壁橱点-
print(neigh.kneighbors([[.5, 1., 1.5]])
Output
输出量
(array([[1.7]]), array([[1]], dtype = int64))
一类SVM (One-Class SVM)
The One-Class SVM, introduced by Schölkopf et al., is the unsupervised Outlier Detection. It is also very efficient in high-dimensional data and estimates the support of a high-dimensional distribution. It is implemented in the Support Vector Machines module in the Sklearn.svm.OneClassSVM object. For defining a frontier, it requires a kernel (mostly used is RBF) and a scalar parameter.
Schölkopf等人介绍的One-Class SVM是无监督的离群值检测。 它在高维数据中也非常有效,并估计了高维分布的支持。 它在Sklearn.svm.OneClassSVM对象的“ 支持向量机”模块中实现。 为了定义边界,它需要一个内核(最常用的是RBF)和一个标量参数。
For better understanding let's fit our data with svm.OneClassSVM object −
为了更好地理解,让我们将数据与svm.OneClassSVM对象配合起来 -
例 (Example)
from sklearn.svm import OneClassSVM
X = [[0], [0.89], [0.90], [0.91], [1]]
OSVMclf = OneClassSVM(gamma = 'scale').fit(X)
Now, we can get the score_samples for input data as follows −
现在,我们可以获得输入数据的score_samples,如下所示:
OSVMclf.score_samples(X)
输出量 (Output)
array([1.12218594, 1.58645126, 1.58673086, 1.58645127, 1.55713767])
Scikit Learn-K最近邻居(KNN) (Scikit Learn - K-Nearest Neighbors (KNN))
This chapter will help you in understanding the nearest neighbor methods in Sklearn.
本章将帮助您了解Sklearn中最接近的邻居方法。
Neighbor based learning method are of both types namely supervised and unsupervised. Supervised neighbors-based learning can be used for both classification as well as regression predictive problems but, it is mainly used for classification predictive problems in industry.
基于邻居的学习方法有两种类型,即有监督的和无监督的。 有监督的基于邻居的学习既可以用于分类预测问题,也可以用于回归预测问题,但是它主要用于行业中的分类预测问题。
Neighbors based learning methods do not have a specialised training phase and uses all the data for training while classification. It also does not assume anything about the underlying data. That’s the reason they are lazy and non-parametric in nature.
基于邻居的学习方法没有专门的训练阶段,而是在分类时将所有数据用于训练。 它还不假定有关基础数据的任何信息。 这就是它们本质上是惰性和非参数化的原因。
The main principle behind nearest neighbor methods is −
最近邻方法的主要原理是-
To find a predefined number of training samples closet in distance to the new data point
查找距离新数据点最近的壁橱中预定数量的训练样本
Predict the label from these number of training samples.
从这些训练样本数量中预测标签。
Here, the number of samples can be a user-defined constant like in K-nearest neighbor learning or vary based on the local density of point like in radius-based neighbor learning.
在这里,样本数可以是用户定义的常数,例如在K近邻学习中,也可以根据点的局部密度而变化,例如在基于半径的邻居学习中。
sklearn.neighbors模块 (sklearn.neighbors Module)
Scikit-learn have sklearn.neighbors module that provides functionality for both unsupervised and supervised neighbors-based learning methods. As input, the classes in this module can handle either NumPy arrays or scipy.sparse matrices.
Scikit-learn具有sklearn.neighbors模块,该模块为无监督和受监督的基于邻居的学习方法提供功能。 作为输入,此模块中的类可以处理NumPy数组或scipy.sparse矩阵。
算法类型 (Types of algorithms)
Different types of algorithms which can be used in neighbor-based methods’ implementation are as follows −
可以在基于邻居的方法的实现中使用的不同类型的算法如下-
蛮力 (Brute Force)
The brute-force computation of distances between all pairs of points in the dataset provides the most naïve neighbor search implementation. Mathematically, for N samples in D dimensions, brute-force approach scales as 0[DN2]
数据集中所有点对之间距离的强力计算提供了最幼稚的邻居搜索实现。 从数学上来说,对于D个维度上的N个样本,蛮力方法的缩放比例为0 [DN 2 ]
For small data samples, this algorithm can be very useful, but it becomes infeasible as and when number of samples grows. Brute force neighbor search can be enabled by writing the keyword algorithm=’brute’.
对于小数据样本,此算法可能非常有用,但是随着样本数量的增加,它变得不可行。 可以通过编写关键字algorithm ='brute'来启用蛮力邻居搜索。
KD树 (K-D Tree)
One of the tree-based data structures that have been invented to address the computational inefficiencies of the brute-force approach, is KD tree data structure. Basically, the KD tree is a binary tree structure which is called K-dimensional tree. It recursively partitions the parameters space along the data axes by dividing it into nested orthographic regions into which the data points are filled.
为了解决暴力破解方法的计算效率低下而发明的基于树的数据结构之一就是KD树数据结构。 基本上,KD树是一种二叉树结构,称为K维树。 它通过将参数空间划分为嵌套的正交区域(将数据点填充到其中)来沿数据轴递归划分参数空间。
优点 (Advantages)
Following are some advantages of K-D tree algorithm −
以下是KD树算法的一些优点-
Construction is fast − As the partitioning is performed only along the data axes, K-D tree’s construction is very fast.
构造速度快 -由于仅沿数据轴执行分区,因此KD树的构造速度非常快。
Less distance computations − This algorithm takes very less distance computations to determine the nearest neighbor of a query point. It only takes [ ()] distance computations.
更少的距离计算 -该算法只需很少的距离计算即可确定查询点的最近邻居。 它只需要[()]距离的计算。
缺点 (Disadvantages)
Fast for only low-dimensional neighbor searches − It is very fast for low-dimensional (D < 20) neighbor searches but as and when D grow it becomes inefficient. As the partitioning is performed only along the data axes,
仅对低维邻居搜索快速-对低维(D <20)邻居搜索非常快,但是随着D的增长,它变得无效。 由于仅沿数据轴执行分区,
K-D tree neighbor searches can be enabled by writing the keyword algorithm=’kd_tree’.
可以通过编写关键字algorithm ='kd_tree'来启用KD树邻居搜索。
球树 (Ball Tree)
As we know that KD Tree is inefficient in higher dimensions, hence, to address this inefficiency of KD Tree, Ball tree data structure was developed. Mathematically, it recursively divides the data, into nodes defined by a centroid C and radius r, in such a way that each point in the node lies within the hyper-sphere defined by centroid C and radius r. It uses triangle inequality, given below, which reduces the number of candidate points for a neighbor search
$$\arrowvert X+Y\arrowvert\leq \arrowvert X\arrowvert+\arrowvert Y\arrowvert$$众所周知,KD树在高维方面效率低下,因此,为了解决KD树的这种低效率问题,开发了球树数据结构。 在数学上,它将数据递归地划分为质心C和半径r定义的节点,以使节点中的每个点都位于质心C和半径r定义的超球面内。 它使用下面给出的三角形不等式,从而减少了邻居搜索的候选点数
$$ \ arrowvert X + Y \ arrowvert \ leq \ arrowvert X \ arrowvert + \ arrowvert Y \ arrowvert $$优点 (Advantages)
Following are some advantages of Ball Tree algorithm −
以下是Ball Tree算法的一些优点-
Efficient on highly structured data − As ball tree partition the data in a series of nesting hyper-spheres, it is efficient on highly structured data.
高效处理高度结构化的数据 -由于球形树将数据划分为一系列嵌套的超球体,因此对高效处理高度结构化的数据非常有效。
Out-performs KD-tree − Ball tree out-performs KD tree in high dimensions because it has spherical geometry of the ball tree nodes.
表现优于KD树 -球树在高维方面表现优于KD树,因为它具有球树节点的球形几何形状。
缺点 (Disadvantages)
Costly − Partition the data in a series of nesting hyper-spheres makes its construction very costly.
成本高昂 -将数据划分为一系列嵌套的超球体,使其构造非常昂贵。
Ball tree neighbor searches can be enabled by writing the keyword algorithm=’ball_tree’.
可以通过编写关键字algorithm ='ball_tree'来启用球树邻居搜索。
选择最近邻居算法 (Choosing Nearest Neighbors Algorithm)
The choice of an optimal algorithm for a given dataset depends upon the following factors −
给定数据集的最佳算法的选择取决于以下因素-
样本数(N)和维数(D) (Number of samples (N) and Dimensionality (D))
These are the most important factors to be considered while choosing Nearest Neighbor algorithm. It is because of the reasons given below −
这些是选择最近邻居算法时要考虑的最重要因素。 这是由于以下原因-
The query time of Brute Force algorithm grows as O[DN].
蛮力算法的查询时间随着O [DN]的增长而增加。
The query time of Ball tree algorithm grows as O[D log(N)].
球树算法的查询时间随着O [D log(N)]而增长。
The query time of KD tree algorithm changes with D in a strange manner that is very difficult to characterize. When D < 20, the cost is O[D log(N)] and this algorithm is very efficient. On the other hand, it is inefficient in case when D > 20 because the cost increases to nearly O[DN].
KD树算法的查询时间随D的变化而变化,这很难描述。 当D <20时,成本为O [D log(N)],该算法非常有效。 另一方面,在D> 20的情况下效率低下,因为成本增加到接近O [DN]。
数据结构 (Data Structure)
Another factor that affect the performance of these algorithms is intrinsic dimensionality of the data or sparsity of the data. It is because the query times of Ball tree and KD tree algorithms can be greatly influenced by it. Whereas, the query time of Brute Force algorithm is unchanged by data structure. Generally, Ball tree and KD tree algorithms produces faster query time when implanted on sparser data with smaller intrinsic dimensionality.
影响这些算法性能的另一个因素是数据的固有维数或数据的稀疏性。 这是因为球树和KD树算法的查询时间会受到很大的影响。 而蛮力算法的查询时间在数据结构上是不变的。 通常,当植入具有较小固有维数的稀疏数据时,球树和KD树算法会产生更快的查询时间。
邻居数(k) (Number of Neighbors (k))
The number of neighbors (k) requested for a query point affects the query time of Ball tree and KD tree algorithms. Their query time becomes slower as number of neighbors (k) increases. Whereas the query time of Brute Force will remain unaffected by the value of k.
请求一个查询点的邻居数(k)影响Ball树算法和KD树算法的查询时间。 随着邻居数(k)的增加,查询时间变慢。 而蛮力的查询时间将不受k值的影响。
查询点数 (Number of query points)
Because, they need construction phase, both KD tree and Ball tree algorithms will be effective if there are large number of query points. On the other hand, if there are a smaller number of query points, Brute Force algorithm performs better than KD tree and Ball tree algorithms.
因为它们需要构造阶段,所以如果存在大量查询点,则KD树算法和Ball树算法都将有效。 另一方面,如果查询点数量较少,则蛮力算法的性能要优于KD树和Ball树算法。
Scikit学习-KNN学习 (Scikit Learn - KNN Learning)
k-NN (k-Nearest Neighbor), one of the simplest machine learning algorithms, is non-parametric and lazy in nature. Non-parametric means that there is no assumption for the underlying data distribution i.e. the model structure is determined from the dataset. Lazy or instance-based learning means that for the purpose of model generation, it does not require any training data points and whole training data is used in the testing phase.
k-NN(k最近邻)是最简单的机器学习算法之一,本质上是非参数的和惰性的。 非参数意味着没有基础数据分布的假设,即从数据集中确定了模型结构。 惰性或基于实例的学习意味着,出于模型生成的目的,它不需要任何训练数据点,并且在测试阶段会使用整个训练数据。
The k-NN algorithm consist of the following two steps −
k-NN算法包括以下两个步骤-
第1步 (Step 1)
In this step, it computes and stores the k nearest neighbors for each sample in the training set.
在此步骤中,它计算并存储训练集中每个样本的k个最近邻居。
第2步 (Step 2)
In this step, for an unlabeled sample, it retrieves the k nearest neighbors from dataset. Then among these k-nearest neighbors, it predicts the class through voting (class with majority votes wins).
在此步骤中,对于未标记的样本,它将从数据集中检索k个最近的邻居。 然后,在这些k近邻中,它通过投票来预测班级(多数票的班级获胜)。
The module, sklearn.neighbors that implements the k-nearest neighbors algorithm, provides the functionality for unsupervised as well as supervised neighbors-based learning methods.
实现k近邻算法的模块sklearn.neighbors提供了无监督以及基于监督的基于邻居的学习方法的功能。
The unsupervised nearest neighbors implement different algorithms (BallTree, KDTree or Brute Force) to find the nearest neighbor(s) for each sample. This unsupervised version is basically only step 1, which is discussed above, and the foundation of many algorithms (KNN and K-means being the famous one) which require the neighbor search. In simple words, it is Unsupervised learner for implementing neighbor searches.
无监督的最近邻居实施不同的算法(BallTree,KDTree或蛮力)以找到每个样本的最近邻居。 此无监督版本基本上只是上面讨论的步骤1,并且是需要邻居搜索的许多算法(KNN和K-means是著名的算法)的基础。 简而言之,它是用于实施邻居搜索的无监督学习者。
On the other hand, the supervised neighbors-based learning is used for classification as well as regression.
另一方面,基于监督的基于邻居的学习被用于分类和回归。
无监督的KNN学习 (Unsupervised KNN Learning)
As discussed, there exist many algorithms like KNN and K-Means that requires nearest neighbor searches. That is why Scikit-learn decided to implement the neighbor search part as its own “learner”. The reason behind making neighbor search as a separate learner is that computing all pairwise distance for finding a nearest neighbor is obviously not very efficient. Let’s see the module used by Sklearn to implement unsupervised nearest neighbor learning along with example.
如讨论的那样,存在许多需要最近邻居搜索的算法,例如KNN和K-Means。 这就是Scikit-learn决定将邻居搜索部分实现为自己的“学习者”的原因。 进行邻居搜索作为单独的学习者的原因在于,计算所有成对距离来查找最近的邻居显然不是很有效。 让我们看一下Sklearn用于实现无监督的最近邻居学习的模块以及示例。
scikit学习模块 (Scikit-learn module)
sklearn.neighbors.NearestNeighbors is the module used to implement unsupervised nearest neighbor learning. It uses specific nearest neighbor algorithms named BallTree, KDTree or Brute Force. In other words, it acts as a uniform interface to these three algorithms.
sklearn.neighbors.NearestNeighbors是用于实施无监督的最近邻居学习的模块。 它使用名为BallTree,KDTree或蛮力的特定最近邻居算法。 换句话说,它充当这三种算法的统一接口。
参量 (Parameters)
Followings table consist the parameters used by NearestNeighbors module −
跟随表包含NearestNeighbors模块使用的参数-
| Sr.No | Parameter & Description |
|---|---|
| 1 | n_neighbors − int, optional The number of neighbors to get. The default value is 5. |
| 2 | radius − float, optional It limits the distance of neighbors to returns. The default value is 1.0. |
| 3 | algorithm − {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, optional This parameter will take the algorithm (BallTree, KDTree or Brute-force) you want to use to compute the nearest neighbors. If you will provide ‘auto’, it will attempt to decide the most appropriate algorithm based on the values passed to fit method. |
| 4 | leaf_size − int, optional It can affect the speed of the construction & query as well as the memory required to store the tree. It is passed to BallTree or KDTree. Although the optimal value depends on the nature of the problem, its default value is 30. |
| 5 | metric − string or callable It is the metric to use for distance computation between points. We can pass it as a string or callable function. In case of callable function, the metric is called on each pair of rows and the resulting value is recorded. It is less efficient than passing the metric name as a string. We can choose from metric from scikit-learn or scipy.spatial.distance. the valid values are as follows − Scikit-learn − [‘cosine’,’manhattan’,‘Euclidean’, ‘l1’,’l2’, ‘cityblock’] Scipy.spatial.distance − [‘braycurtis’,‘canberra’,‘chebyshev’,‘dice’,‘hamming’,‘jaccard’, ‘correlation’,‘kulsinski’,‘mahalanobis’,‘minkowski’,‘rogerstanimoto’,‘russellrao’, ‘sokalmicheme’,’sokalsneath’, ‘seuclidean’, ‘sqeuclidean’, ‘yule’]. The default metric is ‘Minkowski’. |
| 6 | P − integer, optional It is the parameter for the Minkowski metric. The default value is 2 which is equivalent to using Euclidean_distance(l2). |
| 7 | metric_params − dict, optional This is the additional keyword arguments for the metric function. The default value is None. |
| 8 | N_jobs − int or None, optional It reprsetst the numer of parallel jobs to run for neighbor search. The default value is None. |
| 序号 | 参数及说明 |
|---|---|
| 1个 | n_neighbors − int,可选 得到的邻居数。 预设值为5。 |
| 2 | 半径 -浮动,可选 它限制了邻居到返回的距离。 默认值为1.0。 |
| 3 | 算法 -{'auto','ball_tree','kd_tree','brute'},可选 此参数将采用您要用于计算最近邻居的算法(BallTree,KDTree或蛮力)。 如果提供“自动”,它将尝试根据传递给fit方法的值来决定最合适的算法。 |
| 4 | leaf_size -int,可选 它会影响构建和查询的速度以及存储树所需的内存。 它被传递给BallTree或KDTree。 尽管最佳值取决于问题的性质,但其默认值为30。 |
| 5 | 度量 -字符串或可调用 它是用于点之间距离计算的度量。 我们可以将其作为字符串或可调用函数传递。 如果是可调用函数,则在每对行上调用度量,并记录结果值。 它比将度量标准名称作为字符串传递效率低。 我们可以从scikit-learn或scipy.spatial.distance中选择度量。 有效值如下- Scikit学习-['cosine','manhattan','Euclidean','l1','l2','cityblock'] Scipy.spatial.distance- ['braycurtis','canberra','chebyshev','dice','hamming','jaccard','correlation','kulsinski','mahalanobis','minkowski','rogerstanimoto','russellrao',' sokalmicheme”,“ sokalsneath”,“ seuclidean”,“ sqeuclidean”,“ yule”]。 默认指标为“ Minkowski”。 |
| 6 | P-整数,可选 它是Minkowski指标的参数。 默认值为2,这等效于使用Euclidean_distance(l2)。 |
| 7 | metric_params -dict,可选 这是度量功能的其他关键字参数。 默认值为“无”。 |
| 8 | N_jobs -int或None,可选 它重新设置要运行的并行作业数,以进行邻居搜索。 默认值为“无”。 |
Implementation Example
实施实例
The example below will find the nearest neighbors between two sets of data by using the sklearn.neighbors.NearestNeighbors module.
下面的示例将使用sklearn.neighbors.NearestNeighbors模块在两组数据之间找到最接近的邻居。
First, we need to import the required module and packages −
首先,我们需要导入所需的模块和软件包-
from sklearn.neighbors import NearestNeighbors
import numpy as np
Now, after importing the packages, define the sets of data in between we want to find the nearest neighbors −
现在,在导入包之后,在我们要查找最近的邻居之间定义数据集-
Input_data = np.array([[-1, 1], [-2, 2], [-3, 3], [1, 2], [2, 3], [3, 4],[4, 5]])
Next, apply the unsupervised learning algorithm, as follows −
接下来,应用无监督学习算法,如下所示:
nrst_neigh = NearestNeighbors(n_neighbors = 3, algorithm = 'ball_tree')
Next, fit the model with input data set.
接下来,使用输入数据集拟合模型。
nrst_neigh.fit(Input_data)
Now, find the K-neighbors of data set. It will return the indices and distances of the neighbors of each point.
现在,找到数据集的K邻居。 它将返回每个点的邻居的索引和距离。
distances, indices = nbrs.kneighbors(Input_data)
indices
Output
输出量
array(
[
[0, 1, 3],
[1, 2, 0],
[2, 1, 0],
[3, 4, 0],
[4, 5, 3],
[5, 6, 4],
[6, 5, 4]
], dtype = int64
)
distances
Output
输出量
array(
[
[0. , 1.41421356, 2.23606798],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 2.82842712],
[0. , 1.41421356, 2.23606798],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 2.82842712]
]
)
The above output shows that the nearest neighbor of each point is the point itself i.e. at zero. It is because the query set matches the training set.
上面的输出显示每个点的最近邻居是该点本身,即为零。 这是因为查询集与训练集匹配。
Example
例
We can also show a connection between neighboring points by producing a sparse graph as follows −
我们还可以通过生成如下的稀疏图来显示相邻点之间的连接-
nrst_neigh.kneighbors_graph(Input_data).toarray()
Output
输出量
array(
[
[1., 1., 0., 1., 0., 0., 0.],
[1., 1., 1., 0., 0., 0., 0.],
[1., 1., 1., 0., 0., 0., 0.],
[1., 0., 0., 1., 1., 0., 0.],
[0., 0., 0., 1., 1., 1., 0.],
[0., 0., 0., 0., 1., 1., 1.],
[0., 0., 0., 0., 1., 1., 1.]
]
)
Once we fit the unsupervised NearestNeighbors model, the data will be stored in a data structure based on the value set for the argument ‘algorithm’. After that we can use this unsupervised learner’s kneighbors in a model which requires neighbor searches.
一旦我们拟合了无监督的NearestNeighbors模型,数据将基于为参数'algorithm'设置的值存储在数据结构中。 在此之后,我们可以在需要邻居的搜索模型中使用这种无监督学习者的kneighbors。
Complete working/executable program
完整的工作/可执行程序
from sklearn.neighbors import NearestNeighbors
import numpy as np
Input_data = np.array([[-1, 1], [-2, 2], [-3, 3], [1, 2], [2, 3], [3, 4],[4, 5]])
nrst_neigh = NearestNeighbors(n_neighbors = 3, algorithm='ball_tree')
nrst_neigh.fit(Input_data)
distances, indices = nbrs.kneighbors(Input_data)
indices
distances
nrst_neigh.kneighbors_graph(Input_data).toarray()
监督KNN学习 (Supervised KNN Learning)
The supervised neighbors-based learning is used for following −
基于监督的基于邻居的学习用于-
- Classification, for the data with discrete labels 分类,用于带有离散标签的数据
- Regression, for the data with continuous labels. 回归,用于带有连续标签的数据。
最近邻分类器 (Nearest Neighbor Classifier)
We can understand Neighbors-based classification with the help of following two characteristics −
我们可以借助以下两个特征来了解基于邻居的分类-
- It is computed from a simple majority vote of the nearest neighbors of each point. 它是根据每个点的最近邻居的简单多数票计算得出的。
- It simply stores instances of the training data, that’s why it is a type of non-generalizing learning. 它只是存储训练数据的实例,这就是为什么它是一种非一般性学习的原因。
Scikit学习模块 (Scikit-learn modules)
Followings are the two different types of nearest neighbor classifiers used by scikit-learn −
以下是scikit-learn使用的两种不同类型的最近邻居分类器-
| S.No. | Classifiers & Description |
|---|---|
| 1. | KNeighborsClassifier The K in the name of this classifier represents the k nearest neighbors, where k is an integer value specified by the user. Hence as the name suggests, this classifier implements learning based on the k nearest neighbors. The choice of the value of k is dependent on data. |
| 2. | RadiusNeighborsClassifier The Radius in the name of this classifier represents the nearest neighbors within a specified radius r, where r is a floating-point value specified by the user. Hence as the name suggests, this classifier implements learning based on the number neighbors within a fixed radius r of each training point. |
| 序号 | 分类器和说明 |
|---|---|
| 1。 | KNeighborsClassifier 该分类器名称中的K代表k个最近的邻居,其中k是用户指定的整数值。 因此,顾名思义,该分类器基于k个最近的邻居实现学习。 k值的选择取决于数据。 |
| 2。 | RadiusNeighborsClassifier 此分类器名称中的半径表示指定半径r内最近的邻居,其中r是用户指定的浮点值。 因此,顾名思义,该分类器基于每个训练点的固定半径r内的邻居数来实现学习。 |
最近邻居回归 (Nearest Neighbor Regressor)
It is used in the cases where data labels are continuous in nature. The assigned data labels are computed on the basis on the mean of the labels of its nearest neighbors.
它在数据标签本质上是连续的情况下使用。 所分配的数据标签是基于其最近邻居标签的平均值计算的。
Followings are the two different types of nearest neighbor regressors used by scikit-learn −
以下是scikit-learn使用的两种不同类型的最近邻居回归器-
KNeighborsRegressor (KNeighborsRegressor)
The K in the name of this regressor represents the k nearest neighbors, where k is an integer value specified by the user. Hence, as the name suggests, this regressor implements learning based on the k nearest neighbors. The choice of the value of k is dependent on data. Let’s understand it more with the help of an implementation example.
此回归器名称中的K代表k个最近的邻居,其中k是用户指定的整数值 。 因此,顾名思义,该回归器基于k个最近的邻居实现学习。 k值的选择取决于数据。 让我们借助一个实现示例来进一步了解它。
Followings are the two different types of nearest neighbor regressors used by scikit-learn −
以下是scikit-learn使用的两种不同类型的最近邻居回归器-
实施实例 (Implementation Example)
In this example, we will be implementing KNN on data set named Iris Flower data set by using scikit-learn KNeighborsRegressor.
在此示例中,我们将使用scikit-learn KNeighborsRegressor在名为Iris Flower数据集的数据集上实现KNN。
First, import the iris dataset as follows −
首先,导入虹膜数据集,如下所示:
from sklearn.datasets import load_iris
iris = load_iris()
Now, we need to split the data into training and testing data. We will be using Sklearn train_test_split function to split the data into the ratio of 70 (training data) and 20 (testing data) −
现在,我们需要将数据分为训练和测试数据。 我们将使用Sklearn train_test_split函数将数据分成70(训练数据)和20(测试数据)的比率-
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)
Next, we will be doing data scaling with the help of Sklearn preprocessing module as follows −
接下来,我们将在Sklearn预处理模块的帮助下进行数据缩放-
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
Next, import the KNeighborsRegressor class from Sklearn and provide the value of neighbors as follows.
接下来,从Sklearn导入KNeighborsRegressor类,并按如下所示提供邻居的值。
例 (Example)
import numpy as np
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors = 8)
knnr.fit(X_train, y_train)
输出量 (Output)
KNeighborsRegressor(
algorithm = 'auto', leaf_size = 30, metric = 'minkowski',
metric_params = None, n_jobs = None, n_neighbors = 8, p = 2,
weights = 'uniform'
)
例 (Example)
Now, we can find the MSE (Mean Squared Error) as follows −
现在,我们可以找到MSE(均方误差),如下所示:
print ("The MSE is:",format(np.power(y-knnr.predict(X),4).mean()))
输出量 (Output)
The MSE is: 4.4333349609375
例 (Example)
Now, use it to predict the value as follows −
现在,使用它来预测值,如下所示:
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors = 3)
knnr.fit(X, y)
print(knnr.predict([[2.5]]))
输出量 (Output)
[0.66666667]
完整的工作/可执行程序 (Complete working/executable program)
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
import numpy as np
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=8)
knnr.fit(X_train, y_train)
print ("The MSE is:",format(np.power(y-knnr.predict(X),4).mean()))
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=3)
knnr.fit(X, y)
print(knnr.predict([[2.5]]))
RadiusNeighborsRegressor (RadiusNeighborsRegressor)
The Radius in the name of this regressor represents the nearest neighbors within a specified radius r, where r is a floating-point value specified by the user. Hence as the name suggests, this regressor implements learning based on the number neighbors within a fixed radius r of each training point. Let’s understand it more with the help if an implementation example −
此回归器名称中的半径表示指定半径r内的最近邻居,其中r是用户指定的浮点值。 因此,顾名思义,该回归器基于每个训练点的固定半径r内的邻居数实现学习。 让我们在一个实现示例的帮助下更加了解它-
实施实例 (Implementation Example)
In this example, we will be implementing KNN on data set named Iris Flower data set by using scikit-learn RadiusNeighborsRegressor −
在此示例中,我们将使用scikit-learn RadiusNeighborsRegressor在名为Iris Flower数据集的数据集上实现KNN-
First, import the iris dataset as follows −
首先,导入虹膜数据集,如下所示:
from sklearn.datasets import load_iris
iris = load_iris()
Now, we need to split the data into training and testing data. We will be using Sklearn train_test_split function to split the data into the ratio of 70 (training data) and 20 (testing data) −
现在,我们需要将数据分为训练和测试数据。 我们将使用Sklearn train_test_split函数将数据分成70(训练数据)和20(测试数据)的比率-
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
Next, we will be doing data scaling with the help of Sklearn preprocessing module as follows −
接下来,我们将在Sklearn预处理模块的帮助下进行数据缩放-
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
Next, import the RadiusneighborsRegressor class from Sklearn and provide the value of radius as follows −
接下来,从Sklearn导入RadiusneighborsRegressor类,并提供radius的值,如下所示:
import numpy as np
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius=1)
knnr_r.fit(X_train, y_train)
例 (Example)
Now, we can find the MSE (Mean Squared Error) as follows −
现在,我们可以找到MSE(均方误差),如下所示:
print ("The MSE is:",format(np.power(y-knnr_r.predict(X),4).mean()))
输出量 (Output)
The MSE is: The MSE is: 5.666666666666667
例 (Example)
Now, use it to predict the value as follows −
现在,使用它来预测值,如下所示:
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius=1)
knnr_r.fit(X, y)
print(knnr_r.predict([[2.5]]))
输出量 (Output)
[1.]
完整的工作/可执行程序 (Complete working/executable program)
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
import numpy as np
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius = 1)
knnr_r.fit(X_train, y_train)
print ("The MSE is:",format(np.power(y-knnr_r.predict(X),4).mean()))
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius = 1)
knnr_r.fit(X, y)
print(knnr_r.predict([[2.5]]))
Scikit Learn-朴素贝叶斯分类 (Scikit Learn - Classification with Naïve Bayes)
Naïve Bayes methods are a set of supervised learning algorithms based on applying Bayes’ theorem with a strong assumption that all the predictors are independent to each other i.e. the presence of a feature in a class is independent to the presence of any other feature in the same class. This is naïve assumption that is why these methods are called Naïve Bayes methods.
朴素贝叶斯方法是一组基于贝叶斯定理的有监督学习算法,并强烈假设所有预测变量彼此独立,即,一个类中某个特征的存在独立于同一类中任何其他特征的存在类。 这是天真的假设,因此将这些方法称为天真贝叶斯方法。
Bayes theorem states the following relationship in order to find the posterior probability of class i.e. the probability of a label and some observed features, $P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)$.
$$P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)=\left(\frac{P\lgroup Y\rgroup P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)}{P\left(\begin{array}{c} features\end{array}\right)}\right)$$贝叶斯定理陈述以下关系以便找到类的后验概率,即标签的概率和一些观察到的特征,$ P \ left(\ begin {array} {c} Y \ arrowvert features \ end {array} \ right )$。
$$ P \ left(\ begin {array} {c} Y \ arrowvert features \ end {array} \ right)= \ left(\ frac {P \ lgroup Y \ rgroup P \ left(\ begin {array} {c } features \ arrowvert Y \ end {array} \ right)} {P \ left(\ begin {array} {c} features \ end {array} \ right)} \ right)$$Here, $P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)$ is the posterior probability of class.
在这里,$ P \ left(\ begin {array} {c} Y \ arrowvert features \ end {array} \ right)$是类的后验概率。
$P\left(\begin{array}{c} Y\end{array}\right)$ is the prior probability of class.
$ P \ left(\ begin {array} {c} Y \ end {array} \ right)$是类别的先验概率。
$P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)$ is the likelihood which is the probability of predictor given class.
$ P \ left(\ begin {array} {c} features \ arrowvert Y \ end {array} \ right)$是可能性,这是给定类别的预测变量的概率。
$P\left(\begin{array}{c} features\end{array}\right)$ is the prior probability of predictor.
$ P \ left(\ begin {array} {c} features \ end {array} \ right)$是预测变量的先验概率。
The Scikit-learn provides different naïve Bayes classifiers models namely Gaussian, Multinomial, Complement and Bernoulli. All of them differ mainly by the assumption they make regarding the distribution of $P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)$ i.e. the probability of predictor given class.
Scikit学习提供了不同的朴素贝叶斯分类器模型,即高斯,多项式,补数和伯努利。 所有这些变量的主要区别在于,它们对$ P \ left(\ begin {array} {c} features \ arrowvert Y \ end {array} \ right)$的分布做出假设,即预测变量给定类别的概率。
| Sr.No | Model & Description |
|---|---|
| 1 | Gaussian Naïve Bayes Gaussian Naïve Bayes classifier assumes that the data from each label is drawn from a simple Gaussian distribution. |
| 2 | Multinomial Naïve Bayes It assumes that the features are drawn from a simple Multinomial distribution. |
| 3 | Bernoulli Naïve Bayes The assumption in this model is that the features binary (0s and 1s) in nature. An application of Bernoulli Naïve Bayes classification is Text classification with ‘bag of words’ model |
| 4 | Complement Naïve Bayes It was designed to correct the severe assumptions made by Multinomial Bayes classifier. This kind of NB classifier is suitable for imbalanced data sets |
| 序号 | 型号说明 |
|---|---|
| 1个 | 高斯朴素贝叶斯 高斯朴素贝叶斯分类器假设每个标签的数据均来自简单的高斯分布。 |
| 2 | 多项式朴素贝叶斯 假定特征来自简单的多项式分布。 |
| 3 | 伯努利·朴素贝叶斯 该模型中的假设是,特征本质上是二进制的(0和1)。 BernoulliNaïveBayes分类的一个应用是“单词袋”模型的文本分类 |
| 4 | 补充朴素贝叶斯 它旨在纠正多项式贝叶斯分类器的严格假设。 这种NB分类器适用于不平衡数据集 |
建立朴素贝叶斯分类器 (Building Naïve Bayes Classifier)
We can also apply Naïve Bayes classifier on Scikit-learn dataset. In the example below, we are applying GaussianNB and fitting the breast_cancer dataset of Scikit-leran.
我们还可以在Scikit学习数据集上应用朴素贝叶斯分类器。 在下面的示例中,我们将应用GaussianNB并拟合Scikit-leran的breast_cancer数据集。
例 (Example)
Import Sklearn
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
data = load_breast_cancer()
label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']
print(label_names)
print(labels[0])
print(feature_names[0])
print(features[0])
train, test, train_labels, test_labels = train_test_split(
features,labels,test_size = 0.40, random_state = 42
)
from sklearn.naive_bayes import GaussianNB
GNBclf = GaussianNB()
model = GNBclf.fit(train, train_labels)
preds = GNBclf.predict(test)
print(preds)
输出量 (Output)
[
1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1
1 1 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1
1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0
1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0
1 1 0 1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1
0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1
1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0
1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1
1 1 1 1 0 1 0 0 1 1 0 1
]
The above output consists of a series of 0s and 1s which are basically the predicted values from tumor classes namely malignant and benign.
以上输出由一系列0和1组成,它们基本上是来自肿瘤类别的预测值,即恶性和良性。
Scikit学习-决策树 (Scikit Learn - Decision Trees)
In this chapter, we will learn about learning method in Sklearn which is termed as decision trees.
在本章中,我们将学习称为决策树的Sklearn中的学习方法。
Decisions tress (DTs) are the most powerful non-parametric supervised learning method. They can be used for the classification and regression tasks. The main goal of DTs is to create a model predicting target variable value by learning simple decision rules deduced from the data features. Decision trees have two main entities; one is root node, where the data splits, and other is decision nodes or leaves, where we got final output.
决策树(DTs)是最强大的非参数监督学习方法。 它们可用于分类和回归任务。 DT的主要目标是通过学习从数据特征推导出的简单决策规则来创建预测目标变量值的模型。 决策树有两个主要实体。 一个是根节点,数据在其中拆分,另一个是决策节点或叶子,在此处获得最终输出。
决策树算法 (Decision Tree Algorithms)
Different Decision Tree algorithms are explained below −
下面解释了不同的决策树算法-
ID3 (ID3)
It was developed by Ross Quinlan in 1986. It is also called Iterative Dichotomiser 3. The main goal of this algorithm is to find those categorical features, for every node, that will yield the largest information gain for categorical targets.
它由Ross Quinlan在1986年开发。它也称为迭代二分法3。此算法的主要目标是为每个节点找到那些分类特征,这些分类特征将为分类目标产生最大的信息增益。
It lets the tree to be grown to their maximum size and then to improve the tree’s ability on unseen data, applies a pruning step. The output of this algorithm would be a multiway tree.
它使树生长到最大大小,然后为了提高树在看不见数据上的能力,请执行修剪步骤。 该算法的输出将是多路树。
C4.5 (C4.5)
It is the successor to ID3 and dynamically defines a discrete attribute that partition the continuous attribute value into a discrete set of intervals. That’s the reason it removed the restriction of categorical features. It converts the ID3 trained tree into sets of ‘IF-THEN’ rules.
它是ID3的继承者,它动态定义了一个离散属性,该属性将连续属性值划分为一组离散的间隔。 这就是它消除了分类功能限制的原因。 它将经过ID3训练的树转换为“ IF-THEN”规则集。
In order to determine the sequence in which these rules should applied, the accuracy of each rule will be evaluated first.
为了确定应用这些规则的顺序,将首先评估每个规则的准确性。
C5.0 (C5.0)
It works similar as C4.5 but it uses less memory and build smaller rulesets. It is more accurate than C4.5.
它的工作方式与C4.5类似,但使用的内存更少,构建的规则集更小。 它比C4.5更准确。
大车 (CART)
It is called Classification and Regression Trees alsgorithm. It basically generates binary splits by using the features and threshold yielding the largest information gain at each node (called the Gini index).
这称为分类和回归树算法。 它基本上通过使用特征和阈值来生成二进制拆分,从而在每个节点上产生最大的信息增益(称为基尼索引)。
Homogeneity depends upon Gini index, higher the value of Gini index, higher would be the homogeneity. It is like C4.5 algorithm, but, the difference is that it does not compute rule sets and does not support numerical target variables (regression) as well.
同质性取决于基尼系数,基尼系数的值越高,同质性越高。 就像C4.5算法一样,但是区别在于它不计算规则集,也不支持数字目标变量(回归)。
决策树分类 (Classification with decision trees)
In this case, the decision variables are categorical.
在这种情况下,决策变量是分类的。
Sklearn Module − The Scikit-learn library provides the module name DecisionTreeClassifier for performing multiclass classification on dataset.
Sklearn模块 -Scikit-learn库提供模块名称DecisionTreeClassifier,用于对数据集执行多类分类。
参量 (Parameters)
Following table consist the parameters used by sklearn.tree.DecisionTreeClassifier module −
下表包含sklearn.tree.DecisionTreeClassifier模块使用的参数-
| Sr.No | Parameter & Description |
|---|---|
| 1 | criterion − string, optional default= “gini” It represents the function to measure the quality of a split. Supported criteria are “gini” and “entropy”. The default is gini which is for Gini impurity while entropy is for the information gain. |
| 2 | splitter − string, optional default= “best” It tells the model, which strategy from “best” or “random” to choose the split at each node. |
| 3 | max_depth − int or None, optional default=None This parameter decides the maximum depth of the tree. The default value is None which means the nodes will expand until all leaves are pure or until all leaves contain less than min_smaples_split samples. |
| 4 | min_samples_split − int, float, optional default=2 This parameter provides the minimum number of samples required to split an internal node. |
| 5 | min_samples_leaf − int, float, optional default=1 This parameter provides the minimum number of samples required to be at a leaf node. |
| 6 | min_weight_fraction_leaf − float, optional default=0. With this parameter, the model will get the minimum weighted fraction of the sum of weights required to be at a leaf node. |
| 7 | max_features − int, float, string or None, optional default=None It gives the model the number of features to be considered when looking for the best split. |
| 8 | random_state − int, RandomState instance or None, optional, default = none This parameter represents the seed of the pseudo random number generated which is used while shuffling the data. Followings are the options −
|
| 9 | max_leaf_nodes − int or None, optional default=None This parameter will let grow a tree with max_leaf_nodes in best-first fashion. The default is none which means there would be unlimited number of leaf nodes. |
| 10 | min_impurity_decrease − float, optional default=0. This value works as a criterion for a node to split because the model will split a node if this split induces a decrease of the impurity greater than or equal to min_impurity_decrease value. |
| 11 | min_impurity_split − float, default=1e-7 It represents the threshold for early stopping in tree growth. |
| 12 | class_weight − dict, list of dicts, “balanced” or None, default=None It represents the weights associated with classes. The form is {class_label: weight}. If we use the default option, it means all the classes are supposed to have weight one. On the other hand, if you choose class_weight: balanced, it will use the values of y to automatically adjust weights. |
| 13 | presort − bool, optional default=False It tells the model whether to presort the data to speed up the finding of best splits in fitting. The default is false but of set to true, it may slow down the training process. |
| 序号 | 参数及说明 |
|---|---|
| 1个 | 条件 -字符串,可选默认值=“ gini” 它代表测量分割质量的功能。 支持的标准是“基尼”和“熵”。 默认值为基尼,它用于基尼杂质,而熵用于信息增益。 |
| 2 | splitter-字符串,可选默认值=“ best” 它告诉模型,从“最佳”或“随机”中选择哪种策略在每个节点上选择拆分。 |
| 3 | max_depth -int或无,可选默认值=无 此参数确定树的最大深度。 默认值为None(无),这意味着节点将一直扩展,直到所有叶子都是纯净的,或者直到所有叶子都包含少于min_smaples_split个样本。 |
| 4 | min_samples_split -int,float,可选默认值= 2 此参数提供拆分内部节点所需的最少样本数。 |
| 5 | min_samples_leaf -int,float,可选默认值= 1 此参数提供了在叶节点处所需的最少样本数。 |
| 6 | min_weight_fraction_leaf-浮点数,可选默认值= 0。 使用此参数,模型将获得在叶节点处所需的权重总和的最小加权分数。 |
| 7 | max_features -int,float,string或None,可选默认值= None 它为模型提供了寻找最佳分割时要考虑的特征数量。 |
| 8 | random_state -int,RandomState实例或无,可选,默认=无 此参数表示生成的伪随机数的种子,在对数据进行混洗时会使用该种子。 以下是选项-
|
| 9 | max_leaf_nodes -int或无,可选默认值=无 此参数将以最佳优先方式使带有max_leaf_nodes的树生长。 默认值为none,这意味着将有无限数量的叶节点。 |
| 10 | min_impurity_decrease-浮动,可选默认值= 0。 该值用作节点拆分的标准,因为如果该拆分导致杂质减少量大于或等于min_impurity_decrease值,则模型将拆分节点。 |
| 11 | min_impurity_split-浮点数,默认= 1e-7 它代表了树木生长尽早停止的门槛。 |
| 12 | class_weight-字典,字典列表,“平衡”或“无”,默认=无 它表示与类关联的权重。 格式为{class_label:weight}。 如果使用默认选项,则意味着所有类都应具有权重一。 另一方面,如果选择class_weight:balanced ,它将使用y的值自动调整权重。 |
| 13 | 预排序-bool ,可选默认值= False 它告诉模型是否对数据进行预排序,以加快找到最佳拟合拟合的速度。 默认值为false,但设置为true,则可能会减慢训练过程。 |
属性 (Attributes)
Following table consist the attributes used by sklearn.tree.DecisionTreeClassifier module −
下表包含sklearn.tree.DecisionTreeClassifier模块使用的属性-
| Sr.No | Parameter & Description |
|---|---|
| 1 | feature_importances_ − array of shape =[n_features] This attribute will return the feature importance. |
| 2 | classes_: − array of shape = [n_classes] or a list of such arrays It represents the classes labels i.e. the single output problem, or a list of arrays of class labels i.e. multi-output problem. |
| 3 | max_features_ − int It represents the deduced value of max_features parameter. |
| 4 | n_classes_ − int or list It represents the number of classes i.e. the single output problem, or a list of number of classes for every output i.e. multi-output problem. |
| 5 | n_features_ − int It gives the number of features when fit() method is performed. |
| 6 | n_outputs_ − int It gives the number of outputs when fit() method is performed. |
| 序号 | 参数及说明 |
|---|---|
| 1个 | feature_importances_-形状数组= [n_features] 此属性将返回功能重要性。 |
| 2 | classes_: −形状数组= [n_classes]或此类数组的列表 它代表类标签,即单个输出问题,或类标签数组的列表,即多输出问题。 |
| 3 | max_features_ − int 它代表max_features参数的推导值。 |
| 4 | n_classes_-整数或列表 它代表类的数量,即单个输出问题,或代表每个输出的类的数量列表,即多输出问题。 |
| 5 | n_features_ − int 它给出了执行fit()方法时的功能数量。 |
| 6 | n_outputs_-整数 它给出了执行fit()方法时的输出数量。 |
方法 (Methods)
Following table consist the methods used by sklearn.tree.DecisionTreeClassifier module −
下表包含sklearn.tree.DecisionTreeClassifier模块使用的方法-
| Sr.No | Parameter & Description |
|---|---|
| 1 | apply(self, X[, check_input]) This method will return the index of the leaf. |
| 2 | decision_path(self, X[, check_input]) As name suggests, this method will return the decision path in the tree |
| 3 | fit(self, X, y[, sample_weight, …]) fit() method will build a decision tree classifier from given training set (X, y). |
| 4 | get_depth(self) As name suggests, this method will return the depth of the decision tree |
| 5 | get_n_leaves(self) As name suggests, this method will return the number of leaves of the decision tree. |
| 6 | get_params(self[, deep]) We can use this method to get the parameters for estimator. |
| 7 | predict(self, X[, check_input]) It will predict class value for X. |
| 8 | predict_log_proba(self, X) It will predict class log-probabilities of the input samples provided by us, X. |
| 9 | predict_proba(self, X[, check_input]) It will predict class probabilities of the input samples provided by us, X. |
| 10 | score(self, X, y[, sample_weight]) As the name implies, the score() method will return the mean accuracy on the given test data and labels.. |
| 11 | set_params(self, \*\*params) We can set the parameters of estimator with this method. |
| 序号 | 参数及说明 |
|---|---|
| 1个 | 申请 (自己,X [,check_input]) 此方法将返回叶子的索引。 |
| 2 | decision_path(个体,X [,check_input]) 顾名思义,此方法将返回树中的决策路径 |
| 3 | 适合 (自我,X,y [,sample_weight,…]) fit()方法将根据给定的训练集(X,y)构建决策树分类器。 |
| 4 | get_depth (个体经营) 顾名思义,此方法将返回决策树的深度 |
| 5 | get_n_leaves (个体) 顾名思义,此方法将返回决策树的叶子数。 |
| 6 | get_params (self [,deep]) 我们可以使用这种方法来获取估计器的参数。 |
| 7 | 预测 (自我,X [,check_input]) 它将预测X的类值。 |
| 8 | Forecast_log_proba (自己,X) 它将预测我们X提供的输入样本的类对数概率。 |
| 9 | 预言_proba (自我,X [,check_input]) 它将预测我们X提供的输入样本的类概率。 |
| 10 | 得分 (自我,X,y [,sample_weight]) 顾名思义,score()方法将返回给定测试数据和标签的平均准确性。 |
| 11 | set_params (self,\ * \ * params) 我们可以用这种方法设置估计器的参数。 |
实施实例 (Implementation Example)
The Python script below will use sklearn.tree.DecisionTreeClassifier module to construct a classifier for predicting male or female from our data set having 25 samples and two features namely ‘height’ and ‘length of hair’ −
下面的Python脚本将使用sklearn.tree.DecisionTreeClassifier模块构造一个分类器,根据我们的数据集中的25个样本和两个特征(“身高”和“头发长度”)来预测男性或女性-
from sklearn import tree
from sklearn.model_selection import train_test_split
X=[[165,19],[175,32],[136,35],[174,65],[141,28],[176,15]
,[131,32],[166,6],[128,32],[179,10],[136,34],[186,2],[12
6,25],[176,28],[112,38],[169,9],[171,36],[116,25],[196,2
5], [196,38], [126,40], [197,20], [150,25], [140,32],[136,35]]
Y=['Man','Woman','Woman','Man','Woman','Man','Woman','Ma
n','Woman','Man','Woman','Man','Woman','Woman','Woman','
Man','Woman','Woman','Man', 'Woman', 'Woman', 'Man', 'Man', 'Woman', 'Woman']
data_feature_names = ['height','length of hair']
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.3, random_state = 1)
DTclf = tree.DecisionTreeClassifier()
DTclf = clf.fit(X,Y)
prediction = DTclf.predict([[135,29]])
print(prediction)
输出量 (Output)
['Woman']
We can also predict the probability of each class by using following python predict_proba() method as follows −
我们还可以通过使用以下python Forecast_proba()方法来预测每个类别的概率,如下所示:
例 (Example)
prediction = DTclf.predict_proba([[135,29]])
print(prediction)
输出量 (Output)
[[0. 1.]]
决策树回归 (Regression with decision trees)
In this case the decision variables are continuous.
在这种情况下,决策变量是连续的。
Sklearn Module − The Scikit-learn library provides the module name DecisionTreeRegressor for applying decision trees on regression problems.
Sklearn模块 -Scikit-learn库提供模块名称DecisionTreeRegressor,用于将决策树应用于回归问题。
参量 (Parameters)
Parameters used by DecisionTreeRegressor are almost same as that were used in DecisionTreeClassifier module. The difference lies in ‘criterion’ parameter. For DecisionTreeRegressor modules ‘criterion: string, optional default= “mse”’ parameter have the following values −
DecisionTreeRegressor使用的参数与DecisionTreeClassifier模块中使用的参数几乎相同。 区别在于“标准”参数。 对于DecisionTreeRegressor模块的'criterion :string,可选的default =“ mse”'参数具有以下值-
mse − It stands for the mean squared error. It is equal to variance reduction as feature selectin criterion. It minimises the L2 loss using the mean of each terminal node.
mse-代表均方误差。 它等于方差减少作为特征选择准则。 它使用每个终端节点的平均值将L2损耗降至最低。
freidman_mse − It also uses mean squared error but with Friedman’s improvement score.
freidman_mse-它也使用均方误差,但具有弗里德曼的改善得分。
mae − It stands for the mean absolute error. It minimizes the L1 loss using the median of each terminal node.
mae-代表平均绝对误差。 它使用每个终端节点的中值将L1损耗降至最低。
Another difference is that it does not have ‘class_weight’ parameter.
另一个区别是它没有'class_weight'参数。
属性 (Attributes)
Attributes of DecisionTreeRegressor are also same as that were of DecisionTreeClassifier module. The difference is that it does not have ‘classes_’ and ‘n_classes_’ attributes.
DecisionTreeRegressor的属性也与DecisionTreeClassifier模块的属性相同。 区别在于它不具有'classes_'和'n_classes_ '属性。
方法 (Methods)
Methods of DecisionTreeRegressor are also same as that were of DecisionTreeClassifier module. The difference is that it does not have ‘predict_log_proba()’ and ‘predict_proba()’’ attributes.
DecisionTreeRegressor的方法也与DecisionTreeClassifier模块的方法相同。 区别在于它不具有'predict_log_proba()'和'predict_proba()' '属性。
实施实例 (Implementation Example)
The fit() method in Decision tree regression model will take floating point values of y. let’s see a simple implementation example by using Sklearn.tree.DecisionTreeRegressor −
决策树回归模型中的fit()方法将采用y的浮点值。 我们来看一个使用Sklearn.tree.DecisionTreeRegressor的简单实现示例-
from sklearn import tree
X = [[1, 1], [5, 5]]
y = [0.1, 1.5]
DTreg = tree.DecisionTreeRegressor()
DTreg = clf.fit(X, y)
Once fitted, we can use this regression model to make prediction as follows −
拟合后,我们可以使用此回归模型进行如下预测:
DTreg.predict([[4, 5]])
输出量 (Output)
array([1.5])
Scikit学习-随机决策树 (Scikit Learn - Randomized Decision Trees)
This chapter will help you in understanding randomized decision trees in Sklearn.
本章将帮助您了解Sklearn中的随机决策树。
随机决策树算法 (Randomized Decision Tree algorithms)
As we know that a DT is usually trained by recursively splitting the data, but being prone to overfit, they have been transformed to random forests by training many trees over various subsamples of the data. The sklearn.ensemble module is having following two algorithms based on randomized decision trees −
众所周知,DT通常是通过递归拆分数据来训练的,但是容易过度拟合,通过在数据的各个子样本上训练许多树,可以将它们转换为随机森林。 sklearn.ensemble模块具有以下两种基于随机决策树的算法-
随机森林算法 (The Random Forest algorithm)
For each feature under consideration, it computes the locally optimal feature/split combination. In Random forest, each decision tree in the ensemble is built from a sample drawn with replacement from the training set and then gets the prediction from each of them and finally selects the best solution by means of voting. It can be used for both classification as well as regression tasks.
对于考虑中的每个特征,它都会计算局部最优特征/分割组合。 在随机森林中,集合中的每个决策树都是根据从训练集中替换而来的样本构建的,然后从每个样本中获取预测,最后通过投票选择最佳解决方案。 它可以用于分类以及回归任务。
随机森林分类 (Classification with Random Forest)
For creating a random forest classifier, the Scikit-learn module provides sklearn.ensemble.RandomForestClassifier. While building random forest classifier, the main parameters this module uses are ‘max_features’ and ‘n_estimators’.
为了创建随机森林分类器,Scikit-learn模块提供了sklearn.ensemble.RandomForestClassifier 。 在构建随机森林分类器时,此模块使用的主要参数是'max_features'和'n_estimators' 。
Here, ‘max_features’ is the size of the random subsets of features to consider when splitting a node. If we choose this parameter’s value to none then it will consider all the features rather than a random subset. On the other hand, n_estimators are the number of trees in the forest. The higher the number of trees, the better the result will be. But it will take longer to compute also.
在这里, “ max_features”是分割节点时要考虑的特征随机子集的大小。 如果我们将此参数的值选择为none,则它将考虑所有功能,而不是随机子集。 另一方面, n_estimators是森林中树木的数量。 树的数量越多,结果越好。 但是计算也需要更长的时间。
实施实例 (Implementation example)
In the following example, we are building a random forest classifier by using sklearn.ensemble.RandomForestClassifier and also checking its accuracy also by using cross_val_score module.
在下面的示例中,我们将使用sklearn.ensemble.RandomForestClassifier构建一个随机森林分类器,并使用cross_val_score模块检查其准确性。
from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier
X, y = make_blobs(n_samples = 10000, n_features = 10, centers = 100,random_state = 0) RFclf = RandomForestClassifier(n_estimators = 10,max_depth = None,min_samples_split = 2, random_state = 0)
scores = cross_val_score(RFclf, X, y, cv = 5)
scores.mean()
输出量 (Output)
0.9997
例 (Example)
We can also use the sklearn dataset to build Random Forest classifier. As in the following example we are using iris dataset. We will also find its accuracy score and confusion matrix.
我们还可以使用sklearn数据集构建随机森林分类器。 如以下示例所示,我们使用虹膜数据集。 我们还将找到其准确性得分和混淆矩阵。
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
path = "https://archive.ics.uci.edu/ml/machine-learning-database
s/iris/iris.data"
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
dataset = pd.read_csv(path, names = headernames)
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30)
RFclf = RandomForestClassifier(n_estimators = 50)
RFclf.fit(X_train, y_train)
y_pred = RFclf.predict(X_test)
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)
输出量 (Output)
Confusion Matrix:
[[14 0 0]
[ 0 18 1]
[ 0 0 12]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 14
Iris-versicolor 1.00 0.95 0.97 19
Iris-virginica 0.92 1.00 0.96 12
micro avg 0.98 0.98 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
Accuracy: 0.9777777777777777
随机森林回归 (Regression with Random Forest)
For creating a random forest regression, the Scikit-learn module provides sklearn.ensemble.RandomForestRegressor. While building random forest regressor, it will use the same parameters as used by sklearn.ensemble.RandomForestClassifier.
为了创建随机森林回归,Scikit-learn模块提供了sklearn.ensemble.RandomForestRegressor 。 在构建随机森林回归器时,它将使用与sklearn.ensemble.RandomForestClassifier相同的参数。
实施实例 (Implementation example)
In the following example, we are building a random forest regressor by using sklearn.ensemble.RandomForestregressor and also predicting for new values by using predict() method.
在下面的示例中,我们将使用sklearn.ensemble.RandomForestregressor构建一个随机森林回归器,并且还将通过使用prepare ()方法预测新值。
from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
RFregr = RandomForestRegressor(max_depth = 10,random_state = 0,n_estimators = 100)
RFregr.fit(X, y)
输出量 (Output)
RandomForestRegressor(
bootstrap = True, criterion = 'mse', max_depth = 10,
max_features = 'auto', max_leaf_nodes = None,
min_impurity_decrease = 0.0, min_impurity_split = None,
min_samples_leaf = 1, min_samples_split = 2,
min_weight_fraction_leaf = 0.0, n_estimators = 100, n_jobs = None,
oob_score = False, random_state = 0, verbose = 0, warm_start = False
)
Once fitted we can predict from regression model as follows −
一旦拟合,我们可以从回归模型预测如下:
print(RFregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))
输出量 (Output)
[98.47729198]
额外树方法 (Extra-Tree Methods)
For each feature under consideration, it selects a random value for the split. The benefit of using extra tree methods is that it allows to reduce the variance of the model a bit more. The disadvantage of using these methods is that it slightly increases the bias.
对于考虑中的每个功能,它都会为分割选择一个随机值。 使用额外的树方法的好处在于,它可以进一步减少模型的方差。 使用这些方法的缺点是它会稍微增加偏差。
额外树法分类 (Classification with Extra-Tree Method)
For creating a classifier using Extra-tree method, the Scikit-learn module provides sklearn.ensemble.ExtraTreesClassifier. It uses the same parameters as used by sklearn.ensemble.RandomForestClassifier. The only difference is in the way, discussed above, they build trees.
为了使用Extra-tree方法创建分类器,Scikit-learn模块提供了sklearn.ensemble.ExtraTreesClassifier 。 它使用与sklearn.ensemble.RandomForestClassifier相同的参数。 唯一的区别在于,它们在构建树木的方式如上所述。
实施实例 (Implementation example)
In the following example, we are building a random forest classifier by using sklearn.ensemble.ExtraTreeClassifier and also checking its accuracy by using cross_val_score module.
在以下示例中,我们将使用sklearn.ensemble.ExtraTreeClassifier构建一个随机森林分类器,并使用cross_val_score模块检查其准确性。
from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import ExtraTreesClassifier
X, y = make_blobs(n_samples = 10000, n_features = 10, centers=100,random_state = 0)
ETclf = ExtraTreesClassifier(n_estimators = 10,max_depth = None,min_samples_split = 10, random_state = 0)
scores = cross_val_score(ETclf, X, y, cv = 5)
scores.mean()
输出量 (Output)
1.0
例 (Example)
We can also use the sklearn dataset to build classifier using Extra-Tree method. As in the following example we are using Pima-Indian dataset.
我们还可以使用sklearn数据集通过Extra-Tree方法构建分类器。 如以下示例所示,我们使用的是Pima-Indian数据集。
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import ExtraTreesClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 7
kfold = KFold(n_splits=10, random_state=seed)
num_trees = 150
max_features = 5
ETclf = ExtraTreesClassifier(n_estimators=num_trees, max_features=max_features)
results = cross_val_score(ETclf, X, Y, cv=kfold)
print(results.mean())
输出量 (Output)
0.7551435406698566
额外树法回归 (Regression with Extra-Tree Method)
For creating a Extra-Tree regression, the Scikit-learn module provides sklearn.ensemble.ExtraTreesRegressor. While building random forest regressor, it will use the same parameters as used by sklearn.ensemble.ExtraTreesClassifier.
为了创建Extra-Tree回归,Scikit-learn模块提供了sklearn.ensemble.ExtraTreesRegressor 。 在构建随机森林回归器时,它将使用与sklearn.ensemble.ExtraTreesClassifier相同的参数。
实施实例 (Implementation example)
In the following example, we are applying sklearn.ensemble.ExtraTreesregressor and on the same data as we used while creating random forest regressor. Let’s see the difference in the Output
在以下示例中,我们将sklearn.ensemble.ExtraTreesregressor应用于创建随机森林回归器时所使用的相同数据。 让我们看看输出的区别
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
ETregr = ExtraTreesRegressor(max_depth = 10,random_state = 0,n_estimators = 100)
ETregr.fit(X, y)
输出量 (Output)
ExtraTreesRegressor(bootstrap = False, criterion = 'mse', max_depth = 10,
max_features = 'auto', max_leaf_nodes = None,
min_impurity_decrease = 0.0, min_impurity_split = None,
min_samples_leaf = 1, min_samples_split = 2,
min_weight_fraction_leaf = 0.0, n_estimators = 100, n_jobs = None,
oob_score = False, random_state = 0, verbose = 0, warm_start = False)
例 (Example)
Once fitted we can predict from regression model as follows −
一旦拟合,我们可以从回归模型预测如下:
print(ETregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))
输出量 (Output)
[85.50955817]
Scikit学习-促进方法 (Scikit Learn - Boosting Methods)
In this chapter, we will learn about the boosting methods in Sklearn, which enables building an ensemble model.
在本章中,我们将学习Sklearn中的增强方法,该方法可以构建集成模型。
Boosting methods build ensemble model in an increment way. The main principle is to build the model incrementally by training each base model estimator sequentially. In order to build powerful ensemble, these methods basically combine several week learners which are sequentially trained over multiple iterations of training data. The sklearn.ensemble module is having following two boosting methods.
Boosting方法以增量方式构建集成模型。 主要原理是通过顺序地训练每个基本模型估计量来逐步构建模型。 为了建立强大的整体,这些方法基本上结合了几个星期的学习者,这些学习者在训练数据的多次迭代中被顺序训练。 sklearn.ensemble模块具有以下两种增强方法。
AdaBoost (AdaBoost)
It is one of the most successful boosting ensemble method whose main key is in the way they give weights to the instances in dataset. That’s why the algorithm needs to pay less attention to the instances while constructing subsequent models.
它是最成功的增强合奏方法之一,其主要关键在于它们对数据集中的实例赋予权重的方式。 这就是为什么在构建后续模型时,算法需要较少关注实例的原因。
使用AdaBoost进行分类 (Classification with AdaBoost)
For creating a AdaBoost classifier, the Scikit-learn module provides sklearn.ensemble.AdaBoostClassifier. While building this classifier, the main parameter this module use is base_estimator. Here, base_estimator is the value of the base estimator from which the boosted ensemble is built. If we choose this parameter’s value to none then, the base estimator would be DecisionTreeClassifier(max_depth=1).
为了创建AdaBoost分类器,Scikit-learn模块提供了sklearn.ensemble.AdaBoostClassifier 。 在构建此分类器时,此模块使用的主要参数是base_estimator 。 在这里,base_estimator是构建增强后的集合的基础估算器的值。 如果我们将此参数的值选择为none,则基本估计量将为DecisionTreeClassifier(max_depth = 1) 。
实施实例 (Implementation example)
In the following example, we are building a AdaBoost classifier by using sklearn.ensemble.AdaBoostClassifier and also predicting and checking its score.
在以下示例中,我们将使用sklearn.ensemble.AdaBoostClassifier构建AdaBoost分类器,并预测并检查其得分。
from sklearn.ensemble import AdaBoostClassifier
from sklearn.datasets import make_classification
X, y = make_classification(n_samples = 1000, n_features = 10,n_informative = 2, n_redundant = 0,random_state = 0, shuffle = False)
ADBclf = AdaBoostClassifier(n_estimators = 100, random_state = 0)
ADBclf.fit(X, y)
输出量 (Output)
AdaBoostClassifier(algorithm = 'SAMME.R', base_estimator = None,
learning_rate = 1.0, n_estimators = 100, random_state = 0)
例 (Example)
Once fitted, we can predict for new values as follows −
拟合后,我们可以预测新值,如下所示:
print(ADBclf.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))
输出量 (Output)
[1]
例 (Example)
Now we can check the score as follows −
现在我们可以检查分数,如下所示:
ADBclf.score(X, y)
输出量 (Output)
0.995
例 (Example)
We can also use the sklearn dataset to build classifier using Extra-Tree method. For example, in an example given below, we are using Pima-Indian dataset.
我们还可以使用sklearn数据集通过Extra-Tree方法构建分类器。 例如,在下面给出的示例中,我们使用的是Pima-Indian数据集。
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import AdaBoostClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names = headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 5
kfold = KFold(n_splits = 10, random_state = seed)
num_trees = 100
max_features = 5
ADBclf = AdaBoostClassifier(n_estimators = num_trees, max_features = max_features)
results = cross_val_score(ADBclf, X, Y, cv = kfold)
print(results.mean())
输出量 (Output)
0.7851435406698566
使用AdaBoost回归 (Regression with AdaBoost)
For creating a regressor with Ada Boost method, the Scikit-learn library provides sklearn.ensemble.AdaBoostRegressor. While building regressor, it will use the same parameters as used by sklearn.ensemble.AdaBoostClassifier.
为了使用Ada Boost方法创建回归器,Scikit-learn库提供了sklearn.ensemble.AdaBoostRegressor 。 在构建回归器时,它将使用与sklearn.ensemble.AdaBoostClassifier相同的参数。
实施实例 (Implementation example)
In the following example, we are building a AdaBoost regressor by using sklearn.ensemble.AdaBoostregressor and also predicting for new values by using predict() method.
在下面的示例中,我们将使用sklearn.ensemble.AdaBoostregressor构建AdaBoost回归变量,并使用predict()方法预测新值。
from sklearn.ensemble import AdaBoostRegressor
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False)
ADBregr = RandomForestRegressor(random_state = 0,n_estimators = 100)
ADBregr.fit(X, y)
输出量 (Output)
AdaBoostRegressor(base_estimator = None, learning_rate = 1.0, loss = 'linear',
n_estimators = 100, random_state = 0)
例 (Example)
Once fitted we can predict from regression model as follows −
一旦拟合,我们可以从回归模型预测如下:
print(ADBregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))
输出量 (Output)
[85.50955817]
梯度树增强 (Gradient Tree Boosting)
It is also called Gradient Boosted Regression Trees (GRBT). It is basically a generalization of boosting to arbitrary differentiable loss functions. It produces a prediction model in the form of an ensemble of week prediction models. It can be used for the regression and classification problems. Their main advantage lies in the fact that they naturally handle the mixed type data.
也称为梯度增强回归树 (GRBT)。 从根本上讲,它是推广到任意微分损失函数的一般化。 它以周预测模型的集合的形式生成预测模型。 它可以用于回归和分类问题。 它们的主要优点在于它们自然地处理混合类型数据。
使用梯度树增强进行分类 (Classification with Gradient Tree Boost)
For creating a Gradient Tree Boost classifier, the Scikit-learn module provides sklearn.ensemble.GradientBoostingClassifier. While building this classifier, the main parameter this module use is ‘loss’. Here, ‘loss’ is the value of loss function to be optimized. If we choose loss = deviance, it refers to deviance for classification with probabilistic outputs.
为了创建Gradient Tree Boost分类器,Scikit-learn模块提供了sklearn.ensemble.GradientBoostingClassifier 。 在构建此分类器时,此模块使用的主要参数是“损失”。 在此,“损失”是要优化的损失函数的值。 如果我们选择损失=偏差,则它是指偏差与概率输出的分类。
On the other hand, if we choose this parameter’s value to exponential then it recovers the AdaBoost algorithm. The parameter n_estimators will control the number of week learners. A hyper-parameter named learning_rate (in the range of (0.0, 1.0]) will control overfitting via shrinkage.
另一方面,如果我们将此参数的值选择为指数值,则它将恢复AdaBoost算法。 参数n_estimators将控制每周学习者的数量。 名为learning_rate的超参数(在(0.0,1.0]范围内)将通过收缩来控制过度拟合。
实施实例 (Implementation example)
In the following example, we are building a Gradient Boosting classifier by using sklearn.ensemble.GradientBoostingClassifier. We are fitting this classifier with 50 week learners.
在以下示例中,我们通过使用sklearn.ensemble.GradientBoostingClassifier构建一个Gradient Boosting分类器 。 我们正在为该分类器配备50个星期的学习者。
from sklearn.datasets import make_hastie_10_2
from sklearn.ensemble import GradientBoostingClassifier
X, y = make_hastie_10_2(random_state = 0)
X_train, X_test = X[:5000], X[5000:]
y_train, y_test = y[:5000], y[5000:]
GDBclf = GradientBoostingClassifier(n_estimators = 50, learning_rate = 1.0,max_depth = 1, random_state = 0).fit(X_train, y_train)
GDBclf.score(X_test, y_test)
输出量 (Output)
0.8724285714285714
例 (Example)
We can also use the sklearn dataset to build classifier using Gradient Boosting Classifier. As in the following example we are using Pima-Indian dataset.
我们还可以使用sklearn数据集通过Gradient Boosting分类器构建分类器。 如以下示例所示,我们使用的是Pima-Indian数据集。
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import GradientBoostingClassifier
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names = headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
seed = 5
kfold = KFold(n_splits = 10, random_state = seed)
num_trees = 100
max_features = 5
ADBclf = GradientBoostingClassifier(n_estimators = num_trees, max_features = max_features)
results = cross_val_score(ADBclf, X, Y, cv = kfold)
print(results.mean())
输出量 (Output)
0.7946582356674234
用梯度树增强进行回归 (Regression with Gradient Tree Boost)
For creating a regressor with Gradient Tree Boost method, the Scikit-learn library provides sklearn.ensemble.GradientBoostingRegressor. It can specify the loss function for regression via the parameter name loss. The default value for loss is ‘ls’.
为了使用Gradient Tree Boost方法创建回归器,Scikit-learn库提供了sklearn.ensemble.GradientBoostingRegressor 。 它可以通过参数名称loss指定用于回归的损失函数。 损失的默认值为“ ls”。
实施实例 (Implementation example)
In the following example, we are building a Gradient Boosting regressor by using sklearn.ensemble.GradientBoostingregressor and also finding the mean squared error by using mean_squared_error() method.
在下面的示例中,我们将使用sklearn.ensemble.GradientBoostingregressor构建渐变增强回归器,并使用mean_squared_error()方法找到均方误差。
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor
X, y = make_friedman1(n_samples = 2000, random_state = 0, noise = 1.0)
X_train, X_test = X[:1000], X[1000:]
y_train, y_test = y[:1000], y[1000:]
GDBreg = GradientBoostingRegressor(n_estimators = 80, learning_rate=0.1,
max_depth = 1, random_state = 0, loss = 'ls').fit(X_train, y_train)
Once fitted we can find the mean squared error as follows −
拟合后,我们可以找到均方误差,如下所示:
mean_squared_error(y_test, GDBreg.predict(X_test))
输出量 (Output)
5.391246106657164
Scikit Learn-聚类方法 (Scikit Learn - Clustering Methods)
Here, we will study about the clustering methods in Sklearn which will help in identification of any similarity in the data samples.
在这里,我们将研究Sklearn中的聚类方法,这将有助于识别数据样本中的任何相似性。
Clustering methods, one of the most useful unsupervised ML methods, used to find similarity & relationship patterns among data samples. After that, they cluster those samples into groups having similarity based on features. Clustering determines the intrinsic grouping among the present unlabeled data, that’s why it is important.
聚类方法是最有用的无监督ML方法之一,用于查找数据样本之间的相似性和关系模式。 之后,他们将这些样本基于特征聚类为具有相似性的组。 聚类决定了当前未标记数据之间的固有分组,这就是为什么它很重要。
The Scikit-learn library have sklearn.cluster to perform clustering of unlabeled data. Under this module scikit-leran have the following clustering methods −
Scikit-learn库具有sklearn.cluster以执行未标记数据的聚类。 在这个模块下scikit-leran具有以下聚类方法-
均值 (KMeans)
This algorithm computes the centroids and iterates until it finds optimal centroid. It requires the number of clusters to be specified that’s why it assumes that they are already known. The main logic of this algorithm is to cluster the data separating samples in n number of groups of equal variances by minimizing the criteria known as the inertia. The number of clusters identified by algorithm is represented by ‘K.
该算法计算质心并进行迭代,直到找到最佳质心为止。 它要求指定簇的数量,这就是为什么它假定它们已经已知的原因。 该算法的主要逻辑是,通过最小化称为惯性的标准,将分离样本的数据聚类为n个等方差组。 用算法标识的簇数用'K表示。
Scikit-learn have sklearn.cluster.KMeans module to perform K-Means clustering. While computing cluster centers and value of inertia, the parameter named sample_weight allows sklearn.cluster.KMeans module to assign more weight to some samples.
Scikit-learn具有sklearn.cluster.KMeans模块来执行K-Means聚类。 在计算聚类中心和惯性值时,名为sample_weight的参数允许sklearn.cluster.KMeans模块为某些样本分配更多的权重。
亲和力传播 (Affinity Propagation)
This algorithm is based on the concept of ‘message passing’ between different pairs of samples until convergence. It does not require the number of clusters to be specified before running the algorithm. The algorithm has a time complexity of the order (2), which is the biggest disadvantage of it.
该算法基于不同对样本之间的“消息传递”直到收敛的概念。 在运行算法之前,不需要指定群集数。 该算法的时间复杂度约为(2),这是其最大的缺点。
Scikit-learn have sklearn.cluster.AffinityPropagation module to perform Affinity Propagation clustering.
Scikit-learn具有sklearn.cluster.AffinityPropagation模块,以执行Affinity Propagation聚类。
均值漂移 (Mean Shift)
This algorithm mainly discovers blobs in a smooth density of samples. It assigns the datapoints to the clusters iteratively by shifting points towards the highest density of datapoints. Instead of relying on a parameter named bandwidth dictating the size of the region to search through, it automatically sets the number of clusters.
该算法主要发现样本平滑密度中的斑点 。 它通过将数据点移向最高密度的数据点来将数据点迭代地分配给群集。 它会自动设置簇数,而不是依靠一个称为带宽的参数来指示要搜索的区域的大小。
Scikit-learn have sklearn.cluster.MeanShift module to perform Mean Shift clustering.
Scikit-learn具有sklearn.cluster.MeanShift模块来执行均值漂移聚类。
光谱聚类 (Spectral Clustering)
Before clustering, this algorithm basically uses the eigenvalues i.e. spectrum of the similarity matrix of the data to perform dimensionality reduction in fewer dimensions. The use of this algorithm is not advisable when there are large number of clusters.
在聚类之前,该算法基本上使用特征值,即数据相似矩阵的频谱,以较少的维数进行维数减少。 当群集数量很多时,建议不要使用此算法。
Scikit-learn have sklearn.cluster.SpectralClustering module to perform Spectral clustering.
Scikit-learn具有sklearn.cluster.SpectralClustering模块来执行光谱聚类。
层次聚类 (Hierarchical Clustering)
This algorithm builds nested clusters by merging or splitting the clusters successively. This cluster hierarchy is represented as dendrogram i.e. tree. It falls into following two categories −
该算法通过依次合并或拆分群集来构建嵌套群集。 该群集层次结构表示为树状图,即树。 它分为以下两类-
Agglomerative hierarchical algorithms − In this kind of hierarchical algorithm, every data point is treated like a single cluster. It then successively agglomerates the pairs of clusters. This uses the bottom-up approach.
聚集层次算法 -在这种层次算法中,每个数据点都被视为单个群集。 然后,它连续聚集成对的集群。 这使用了自下而上的方法。
Divisive hierarchical algorithms − In this hierarchical algorithm, all data points are treated as one big cluster. In this the process of clustering involves dividing, by using top-down approach, the one big cluster into various small clusters.
划分层次算法 -在此层次算法中,所有数据点都被视为一个大群集。 在此过程中,群集过程涉及通过使用自上而下的方法将一个大群集分为多个小群集。
Scikit-learn have sklearn.cluster.AgglomerativeClustering module to perform Agglomerative Hierarchical clustering.
Scikit-learn具有sklearn.cluster.AgglomerativeClustering模块来执行聚集层次聚类。
数据库扫描 (DBSCAN)
It stands for “Density-based spatial clustering of applications with noise”. This algorithm is based on the intuitive notion of “clusters” & “noise” that clusters are dense regions of the lower density in the data space, separated by lower density regions of data points.
它代表“基于噪声的应用程序的基于密度的空间聚类” 。 该算法基于“集群”和“噪声”的直观概念,即群集是数据空间中密度较低的密集区域,被数据点的密度较低的区域分隔开。
Scikit-learn have sklearn.cluster.DBSCAN module to perform DBSCAN clustering. There are two important parameters namely min_samples and eps used by this algorithm to define dense.
Scikit-learn具有sklearn.cluster.DBSCAN模块来执行DBSCAN集群。 该算法使用两个重要参数,即min_samples和eps来定义稠密度。
Higher value of parameter min_samples or lower value of the parameter eps will give an indication about the higher density of data points which is necessary to form a cluster.
参数min_samples的较高值或参数eps的较低值将指示有关形成群集所必需的较高数据点密度。
光学 (OPTICS)
It stands for “Ordering points to identify the clustering structure”. This algorithm also finds density-based clusters in spatial data. It’s basic working logic is like DBSCAN.
它代表“订购点以识别聚类结构” 。 该算法还可以在空间数据中找到基于密度的聚类。 它的基本工作逻辑就像DBSCAN。
It addresses a major weakness of DBSCAN algorithm-the problem of detecting meaningful clusters in data of varying density-by ordering the points of the database in such a way that spatially closest points become neighbors in the ordering.
它解决了DBSCAN算法的一个主要弱点-通过以使空间上最近的点成为该次序中的邻居的方式对数据库的点进行排序来检测变化密度的数据中有意义的簇的问题。
Scikit-learn have sklearn.cluster.OPTICS module to perform OPTICS clustering.
Scikit-learn具有sklearn.cluster.OPTICS模块来执行OPTICS集群。
桦木 (BIRCH)
It stands for Balanced iterative reducing and clustering using hierarchies. It is used to perform hierarchical clustering over large data sets. It builds a tree named CFT i.e. Characteristics Feature Tree, for the given data.
它代表使用层次结构的平衡迭代减少和聚类。 它用于对大型数据集执行分层聚类。 它为给定的数据构建一个名为CFT的 树 ,即特征特征树 。
The advantage of CFT is that the data nodes called CF (Characteristics Feature) nodes holds the necessary information for clustering which further prevents the need to hold the entire input data in memory.
CFT的优势在于,称为CF(特征功能)节点的数据节点拥有用于群集的必要信息,这进一步避免了将整个输入数据保存在内存中的需求。
Scikit-learn have sklearn.cluster.Birch module to perform BIRCH clustering.
Scikit-learn具有sklearn.cluster.Birch模块来执行BIRCH聚类。
比较聚类算法 (Comparing Clustering Algorithms)
Following table will give a comparison (based on parameters, scalability and metric) of the clustering algorithms in scikit-learn.
下表将对scikit-learn中的聚类算法进行比较(基于参数,可伸缩性和度量)。
| Sr.No | Algorithm Name | Parameters | Scalability | Metric Used |
|---|---|---|---|---|
| 1 | K-Means | No. of clusters | Very large n_samples | The distance between points. |
| 2 | Affinity Propagation | Damping | It’s not scalable with n_samples | Graph Distance |
| 3 | Mean-Shift | Bandwidth | It’s not scalable with n_samples. | The distance between points. |
| 4 | Spectral Clustering | No.of clusters | Medium level of scalability with n_samples. Small level of scalability with n_clusters. | Graph Distance |
| 5 | Hierarchical Clustering | Distance threshold or No.of clusters | Large n_samples Large n_clusters | The distance between points. |
| 6 | DBSCAN | Size of neighborhood | Very large n_samples and medium n_clusters. | Nearest point distance |
| 7 | OPTICS | Minimum cluster membership | Very large n_samples and large n_clusters. | The distance between points. |
| 8 | BIRCH | Threshold, Branching factor | Large n_samples Large n_clusters | The Euclidean distance between points. |
| 序号 | 算法名称 | 参量 | 可扩展性 | 公制使用 |
|---|---|---|---|---|
| 1个 | K均值 | 集群数 | 非常大的n_samples | 点之间的距离。 |
| 2 | 亲和力传播 | 减震 | n_samples无法扩展 | 图形距离 |
| 3 | 均值漂移 | 带宽 | n_samples无法扩展。 | 点之间的距离。 |
| 4 | 光谱聚类 | 簇数 | 具有n_samples的中等级别的可伸缩性。 n_clusters的可伸缩性较小。 | 图形距离 |
| 5 | 层次聚类 | 距离阈值或簇数 | 大n_sample大n_clusters | 点之间的距离。 |
| 6 | 数据库扫描 | 邻里大小 | 非常大的n_samples和中等n_clusters。 | 最近点距离 |
| 7 | 光学 | 最低集群成员 | 非常大的n_samples和大n_clusters。 | 点之间的距离。 |
| 8 | 桦木 | 阈值,分支因子 | 大n_sample大n_clusters | 点之间的欧几里得距离。 |
Scikit学习数字数据集的K均值聚类 (K-Means Clustering on Scikit-learn Digit dataset)
In this example, we will apply K-means clustering on digits dataset. This algorithm will identify similar digits without using the original label information. Implementation is done on Jupyter notebook.
在此示例中,我们将对数字数据集应用K-means聚类。 该算法将在不使用原始标签信息的情况下识别相似的数字。 在Jupyter笔记本上完成实现。
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
输出量 (Output)
1797, 64)
This output shows that digit dataset is having 1797 samples with 64 features.
此输出显示数字数据集具有1797个具有64个特征的样本。
例 (Example)
Now, perform the K-Means clustering as follows −
现在,按以下步骤执行K-Means聚类:
kmeans = KMeans(n_clusters = 10, random_state = 0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape
输出量 (Output)
(10, 64)
This output shows that K-means clustering created 10 clusters with 64 features.
此输出显示K-means聚类创建了具有64个特征的10个聚类。
例 (Example)
fig, ax = plt.subplots(2, 5, figsize = (8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks = [], yticks = [])
axi.imshow(center, interpolation = 'nearest', cmap = plt.cm.binary)
输出量 (Output)
The below output has images showing clusters centers learned by K-Means Clustering.
以下输出的图像显示了通过K-Means聚类学习的聚类中心。
Next, the Python script below will match the learned cluster labels (by K-Means) with the true labels found in them −
接下来,下面的Python脚本将匹配学习到的集群标签(通过K-Means)和在其中找到的真实标签-
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]
We can also check the accuracy with the help of the below mentioned command.
我们还可以借助下面提到的命令检查准确性。
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)
输出量 (Output)
0.7935447968836951
完整的实施实例 (Complete Implementation Example)
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
kmeans = KMeans(n_clusters = 10, random_state = 0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape
fig, ax = plt.subplots(2, 5, figsize = (8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks=[], yticks = [])
axi.imshow(center, interpolation = 'nearest', cmap = plt.cm.binary)
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)
Scikit Learn-集群性能评估 (Scikit Learn - Clustering Performance Evaluation)
There are various functions with the help of which we can evaluate the performance of clustering algorithms.
在各种功能的帮助下,我们可以评估聚类算法的性能。
Following are some important and mostly used functions given by the Scikit-learn for evaluating clustering performance −
以下是Scikit学习提供的一些重要且最常用的函数,用于评估集群性能-
调整后的兰德指数 (Adjusted Rand Index)
Rand Index is a function that computes a similarity measure between two clustering. For this computation rand index considers all pairs of samples and counting pairs that are assigned in the similar or different clusters in the predicted and true clustering. Afterwards, the raw Rand Index score is ‘adjusted for chance’ into the Adjusted Rand Index score by using the following formula −
$$Adjusted\:RI=\left(RI-Expected_{-}RI\right)/\left(max\left(RI\right)-Expected_{-}RI\right)$$兰德指数是一项功能,用于计算两个聚类之间的相似性度量。 对于此计算,兰德指数考虑了在预测和真实聚类中分配给相似或不同聚类中的所有样本对和计数对。 然后,使用以下公式将原始的兰德指数得分“调整为偶然”成调整后的兰德指数得分-
$$ Adjusted \:RI = \ left(RI-Expected _ {-} RI \ right)/ \ left(max \ left(RI \ right)-Expected _ {-} RI \ right)$$It has two parameters namely labels_true, which is ground truth class labels, and labels_pred, which are clusters label to evaluate.
它有两个参数,即labels_true (是基础事实类标签)和labels_pred (它们是要评估的簇标签)。
例 (Example)
from sklearn.metrics.cluster import adjusted_rand_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
adjusted_rand_score(labels_true, labels_pred)
输出量 (Output)
0.4444444444444445
Perfect labeling would be scored 1 and bad labelling or independent labelling is scored 0 or negative.
完美标签的评分为1,不良标签或独立标签的评分为0或否定。
基于互信息的分数 (Mutual Information Based Score)
Mutual Information is a function that computes the agreement of the two assignments. It ignores the permutations. There are following versions available −
互信息是一种计算两个分配的一致性的函数。 它忽略了排列。 有以下可用的版本-
标准化互信息(NMI) (Normalized Mutual Information (NMI))
Scikit learn have sklearn.metrics.normalized_mutual_info_score module.
Scikit学习具有sklearn.metrics.normalized_mutual_info_score模块。
例 (Example)
from sklearn.metrics.cluster import normalized_mutual_info_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
normalized_mutual_info_score (labels_true, labels_pred)
输出量 (Output)
0.7611702597222881
调整后的共同信息(AMI) (Adjusted Mutual Information (AMI))
Scikit learn have sklearn.metrics.adjusted_mutual_info_score module.
Scikit学习具有sklearn.metrics.adjusted_mutual_info_score模块。
例 (Example)
from sklearn.metrics.cluster import adjusted_mutual_info_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
adjusted_mutual_info_score (labels_true, labels_pred)
输出量 (Output)
0.4444444444444448
福克斯-锦葵分数 (Fowlkes-Mallows Score)
The Fowlkes-Mallows function measures the similarity of two clustering of a set of points. It may be defined as the geometric mean of the pairwise precision and recall.
Fowlkes-Mallows函数测量一组点的两个聚类的相似性。 它可以定义为成对精度和查全率的几何平均值。
Mathematically,
$$FMS=\frac{TP}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)}}$$数学上
$$ FMS = \ frac {TP} {\ sqrt {\ left(TP + FP \ right)\ left(TP + FN \ right)}} $$Here, TP = True Positive − number of pair of points belonging to the same clusters in true as well as predicted labels both.
在这里, TP =真实正值 -属于相同簇的真实点对数以及预测的标记数。
FP = False Positive − number of pair of points belonging to the same clusters in true labels but not in the predicted labels.
FP =假阳性 -属于真实标签中的相同簇但不属于预测标签中的点对的数量。
FN = False Negative − number of pair of points belonging to the same clusters in the predicted labels but not in the true labels.
FN =假负 -预测标签中属于同一簇的点对的数量,但不是真实标签中的点。
The Scikit learn has sklearn.metrics.fowlkes_mallows_score module −
Scikit学习具有sklearn.metrics.fowlkes_mallows_score模块-
例 (Example)
from sklearn.metrics.cluster import fowlkes_mallows_score
labels_true = [0, 0, 1, 1, 1, 1]
labels_pred = [0, 0, 2, 2, 3, 3]
fowlkes_mallows__score (labels_true, labels_pred)
输出量 (Output)
0.6546536707079771
轮廓系数 (Silhouette Coefficient)
The Silhouette function will compute the mean Silhouette Coefficient of all samples using the mean intra-cluster distance and the mean nearest-cluster distance for each sample.
Silhouette函数将使用每个样本的平均群集内距离和平均最近群集距离来计算所有样本的平均Silhouette系数。
Mathematically,
$$S=\left(b-a\right)/max\left(a,b\right)$$数学上
$$ S = \左(ba \右)/ max \左(a,b \右)$$Here, a is intra-cluster distance.
在此,a是集群内距离。
and, b is mean nearest-cluster distance.
b是平均最近集群距离。
The Scikit learn have sklearn.metrics.silhouette_score module −
Scikit学习具有sklearn.metrics.silhouette_score模块-
例 (Example)
from sklearn import metrics.silhouette_score
from sklearn.metrics import pairwise_distances
from sklearn import datasets
import numpy as np
from sklearn.cluster import KMeans
dataset = datasets.load_iris()
X = dataset.data
y = dataset.target
kmeans_model = KMeans(n_clusters = 3, random_state = 1).fit(X)
labels = kmeans_model.labels_
silhouette_score(X, labels, metric = 'euclidean')
输出量 (Output)
0.5528190123564091
权变矩阵 (Contingency Matrix)
This matrix will report the intersection cardinality for every trusted pair of (true, predicted). Confusion matrix for classification problems is a square contingency matrix.
此矩阵将报告(真实,预测的)每个受信任对的交集基数。 分类问题的混淆矩阵是平方列联矩阵。
The Scikit learn have sklearn.metrics.contingency_matrix module.
Scikit学习了sklearn.metrics.contingency_matrix模块。
例 (Example)
from sklearn.metrics.cluster import contingency_matrix
x = ["a", "a", "a", "b", "b", "b"]
y = [1, 1, 2, 0, 1, 2]
contingency_matrix(x, y)
输出量 (Output)
array([
[0, 2, 1],
[1, 1, 1]
])
The first row of above output shows that among three samples whose true cluster is “a”, none of them is in 0, two of the are in 1 and 1 is in 2. On the other hand, second row shows that among three samples whose true cluster is “b”, 1 is in 0, 1 is in 1 and 1 is in 2.
上面输出的第一行显示了真实簇为“ a”的三个样本中,没有一个在0中,两个在1中,而1在2中。另一方面,第二行显示了在三个样本中其真实簇为“ b”,1在0中,1在1中,1在2中。
Scikit Learn-使用PCA减少维度 (Scikit Learn - Dimensionality Reduction using PCA)
Dimensionality reduction, an unsupervised machine learning method is used to reduce the number of feature variables for each data sample selecting set of principal features. Principal Component Analysis (PCA) is one of the popular algorithms for dimensionality reduction.
降维是一种无监督的机器学习方法,用于减少选择主要特征的每个数据样本的特征变量的数量。 主成分分析(PCA)是降维的流行算法之一。
精确的PCA (Exact PCA)
Principal Component Analysis (PCA) is used for linear dimensionality reduction using Singular Value Decomposition (SVD) of the data to project it to a lower dimensional space. While decomposition using PCA, input data is centered but not scaled for each feature before applying the SVD.
主成分分析 (PCA)用于线性降维,使用数据的奇异值分解 (SVD)将其投影到较低维度的空间中。 使用PCA进行分解时,在应用SVD之前,输入数据将居中但未按比例缩放。
The Scikit-learn ML library provides sklearn.decomposition.PCA module that is implemented as a transformer object which learns n components in its fit() method. It can also be used on new data to project it on these components.
Scikit-learn ML库提供了sklearn.decomposition.PCA模块,该模块被实现为可在其fit()方法中学习n个组件的转换器对象。 也可以将其用于新数据,以将其投影到这些组件上。
例 (Example)
The below example will use sklearn.decomposition.PCA module to find best 5 Principal components from Pima Indians Diabetes dataset.
以下示例将使用sklearn.decomposition.PCA模块从Pima Indians Diabetes数据集中找到最佳的5个主要成分。
from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\Users\Leekha\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', ‘class']
dataframe = read_csv(path, names = names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
pca = PCA(n_components = 5)
fit = pca.fit(X)
print(("Explained Variance: %s") % (fit.explained_variance_ratio_))
print(fit.components_)
输出量 (Output)
Explained Variance: [0.88854663 0.06159078 0.02579012 0.01308614 0.00744094]
[
[-2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-029.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
[-2.26488861e-02 -9.72210040e-01 -1.41909330e-01 5.78614699e-029.46266913e-02 -4.69729766e-02 -8.16804621e-04 -1.40168181e-01]
[-2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-012.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]
[-4.90459604e-02 1.19830016e-01 -2.62742788e-01 8.84369380e-01-6.55503615e-02 1.92801728e-01 2.69908637e-03 -3.01024330e-01]
[ 1.51612874e-01 -8.79407680e-02 -2.32165009e-01 2.59973487e-01-1.72312241e-04 2.14744823e-02 1.64080684e-03 9.20504903e-01]
]
增量式PCA (Incremental PCA)
Incremental Principal Component Analysis (IPCA) is used to address the biggest limitation of Principal Component Analysis (PCA) and that is PCA only supports batch processing, means all the input data to be processed should fit in the memory.
增量主成分分析 (IPCA)用于解决主成分分析(PCA)的最大局限,即PCA仅支持批处理,这意味着要处理的所有输入数据都应适合内存。
The Scikit-learn ML library provides sklearn.decomposition.IPCA module that makes it possible to implement Out-of-Core PCA either by using its partial_fit method on sequentially fetched chunks of data or by enabling use of np.memmap, a memory mapped file, without loading the entire file into memory.
Scikit-learn ML库提供了sklearn.decomposition.IPCA模块,该模块可以通过对依次提取的数据块使用partial_fit方法或启用内存映射文件np.memmap来实现核外PCA。 ,而不将整个文件加载到内存中。
Same as PCA, while decomposition using IPCA, input data is centered but not scaled for each feature before applying the SVD.
与PCA相同,使用IPCA进行分解时,在应用SVD之前,输入数据居中但未按每个功能缩放。
例 (Example)
The below example will use sklearn.decomposition.IPCA module on Sklearn digit dataset.
以下示例将在Sklearn数字数据集上使用sklearn.decomposition.IPCA模块。
from sklearn.datasets import load_digits
from sklearn.decomposition import IncrementalPCA
X, _ = load_digits(return_X_y = True)
transformer = IncrementalPCA(n_components = 10, batch_size = 100)
transformer.partial_fit(X[:100, :])
X_transformed = transformer.fit_transform(X)
X_transformed.shape
输出量 (Output)
(1797, 10)
Here, we can partially fit on smaller batches of data (as we did on 100 per batch) or you can let the fit() function to divide the data into batches.
在这里,我们可以部分拟合较小的数据批处理(就像我们对每批100个数据所做的那样),也可以让fit()函数将数据分为几批。
内核PCA (Kernel PCA)
Kernel Principal Component Analysis, an extension of PCA, achieves non-linear dimensionality reduction using kernels. It supports both transform and inverse_transform.
内核主成分分析(PCA的扩展)使用内核实现了非线性降维。 它同时支持transform和inverse_transform 。
The Scikit-learn ML library provides sklearn.decomposition.KernelPCA module.
Scikit-learn ML库提供了sklearn.decomposition.KernelPCA模块。
例 (Example)
The below example will use sklearn.decomposition.KernelPCA module on Sklearn digit dataset. We are using sigmoid kernel.
以下示例将在Sklearn数字数据集上使用sklearn.decomposition.KernelPCA模块。 我们正在使用sigmoid内核。
from sklearn.datasets import load_digits
from sklearn.decomposition import KernelPCA
X, _ = load_digits(return_X_y = True)
transformer = KernelPCA(n_components = 10, kernel = 'sigmoid')
X_transformed = transformer.fit_transform(X)
X_transformed.shape
输出量 (Output)
(1797, 10)
使用随机SVD的PCA (PCA using randomized SVD)
Principal Component Analysis (PCA) using randomized SVD is used to project data to a lower-dimensional space preserving most of the variance by dropping the singular vector of components associated with lower singular values. Here, the sklearn.decomposition.PCA module with the optional parameter svd_solver=’randomized’ is going to be very useful.
使用随机SVD的主成分分析(PCA)用于通过删除与较低奇异值关联的成分的奇异矢量来将数据投影到较低维空间,从而保留大部分差异。 在这里,带有可选参数svd_solver ='randomized'的sklearn.decomposition.PCA模块将非常有用。
例 (Example)
The below example will use sklearn.decomposition.PCA module with the optional parameter svd_solver=’randomized’ to find best 7 Principal components from Pima Indians Diabetes dataset.
以下示例将使用带有可选参数svd_solver ='randomized'的sklearn.decomposition.PCA模块,从Pima Indians Diabetes数据集中找到最佳的7个主要成分。
from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\Users\Leekha\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names = names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
pca = PCA(n_components = 7,svd_solver = 'randomized')
fit = pca.fit(X)
print(("Explained Variance: %s") % (fit.explained_variance_ratio_))
print(fit.components_)
输出量 (Output)
Explained Variance: [8.88546635e-01 6.15907837e-02 2.57901189e-02 1.30861374e-027.44093864e-03 3.02614919e-03 5.12444875e-04]
[
[-2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-029.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
[-2.26488861e-02 -9.72210040e-01 -1.41909330e-01 5.78614699e-029.46266913e-02 -4.69729766e-02 -8.16804621e-04 -1.40168181e-01]
[-2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-012.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]
[-4.90459604e-02 1.19830016e-01 -2.62742788e-01 8.84369380e-01-6.55503615e-02 1.92801728e-01 2.69908637e-03 -3.01024330e-01]
[ 1.51612874e-01 -8.79407680e-02 -2.32165009e-01 2.59973487e-01-1.72312241e-04 2.14744823e-02 1.64080684e-03 9.20504903e-01]
[-5.04730888e-03 5.07391813e-02 7.56365525e-02 2.21363068e-01-6.13326472e-03 -9.70776708e-01 -2.02903702e-03 -1.51133239e-02]
[ 9.86672995e-01 8.83426114e-04 -1.22975947e-03 -3.76444746e-041.42307394e-03 -2.73046214e-03 -6.34402965e-03 -1.62555343e-01]
]
翻译自: https://www.tutorialspoint.com/scikit_learn/scikit_learn_quick_guide.htm
scikit-learn