Inception v2/BN-Inception：Batch Normalization 论文笔记

Inception v2 / BN-Inception：Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

摘要：
\quad    \; 各层输入数据分布的变化阻碍了深度网络的训练。这使得训练过程中要设置更低的学习速率，从而减慢了模型的训练；同时使得使用饱和非线性激活函数的模型变得极度难训练。作者将这种现象称为内部协方差变换，并通过normalization层的输入解决了这个问题。文中，作者还提出了mini-batch版的normalization（BN）。BN允许使用更高的学习速率和less careful initialization。BN也是一个regularizer，在某种程度上减轻了dropout的必要性。BN能将当前state of art分类模型的训练steps减少为1/14，并且以明显优势击败了原始模型。

关键点：BN、用两个3x3代替一个5x5、LRN是不必要的。

BN 的好处：

• BN 减少了内部协方差，提高了梯度在网络中的流动，加速了网络的训练。
• BN 使得可以设置更高的学习速率。
• BN 正则了模型。

1.简介

\quad    \; 深度学习在视觉、语音和其它领域方面的state of art提高了许多。随机梯度下降（SGD）已经被证明是训练深度网络的一个高效方法，并且SGD的其它变种，例如momentum和Adagrad已经被使用去获得state of art。SGD优化网络的参数$\Theta$的方法是最小化loss：$$\begin{gathered} \Theta =argmin \\ \Theta \frac{1}{N}\sum _{i=1}^{N}l(x_i,\Theta ) \end{gathered}$$这里$x_{1...N}$是训练集，使用SGD训练时，训练的一个step输入一个batch_size ($m$)的数据$x_{1...m}$。mini-batch被用来计算一个近似梯度：$$\frac{1}{m}\frac{\partial l(x_i,\Theta )}{\partial \Theta }$$ \quad    \; 使用mini-batch个example而不是单个example有很多好处。首先在mini-batch上计算的梯度是整个数据集上计算的梯度的一个近似；mini-batch越大，两者越接近。其次，batch比整个数据集($m$)上计算梯度更高效。

\quad    \; 尽管随机梯度是简单、高效的，但它需要对模型的超参数进行精心地微调，尤其是优化过程中使用的学习速率和模型参数的初始值。每一层的输入都被前面层的参数影响，这使得训练过程变得复杂。模型参数的微小改变会随着网络的加深而放大。

\quad    \; 每一层输入的分布的改变导致一个问题，因为各层需要持续的去适应新的分布。当一个学习系统的输入的分布改变时，据说经历了$covariate$ $shift$2。这通常通过domain adaptation3来处理。但是，协方差变换的概念可以从整个网络扩展到它的部件，例如，一个sub-network或一层。假设一个网络计算：$$l=F_2(F_1(\text{u},{\Theta }_1),{\Theta }_2)$$当$F_1$和$F_2$是任意的变换，参数${\Theta }_1$和${\Theta }_2$是为了最小化loss $l$需要学习的参数。如果假设$x=F_1(\text{u},{\Theta }_1)$，那么学习参数${\Theta }_2$的过程，能够被看作：$$l=F_2(\text{x},{\Theta }_2)$$例如，一个梯度下降step：$${\Theta }_2\leftarrow {\Theta }_2-\frac{\alpha }{m}\sum _{i=1}^m\frac{\partial F_2({\text{x}}_i,{\Theta }_2)}{\partial {\Theta }_2}$$batch size=$m$和学习速率=$\alpha$，上面的公式等价于一个标准的单层网络$F_2(\text{x},{\Theta }_2)$。因此，输入的分布特性使得训练更加更加高效：例如，训练数据和测试数据有相同的分布，同样这个规则也适用于sub-network。如上面所说，x的分布保持不变将是很有益处的。因此，${\Theta }_2$不必重新调整去补偿x的分布的变化。

\quad    \; 固定一个sub-network输入的分布也会对sub-network外的网络产生积极影响。考虑一个使用sigmoid激活函数的层$\text{z}=g(W\text{u}+b)$，这里$\text{u}$是该层的输入，权重矩阵$W$，偏差$b$是该层需要学习的参数，其中$g(x)=\frac{1}{1+exp(-x)}$。随着$|x|$的增加，$g^{\prime }(x)$趋向于0。这意味着$\text{x}=W\text{u}+b$中除$\text{x}$很小的部分，其余梯度将vanish并且模型将会训练的很慢。但是，因为$\text{x}$受$W$和$b$和下面层的参数影响，训练过程中，这些参数的改变将使得$\text{x}$中更多部分移向非线性激活函数的饱和区，从而减慢收敛过程。这一效应会随着网络的加深而放大。在实践中，饱和问题和由此导致的vanishing gradients通常使用ReLU、精心的参数初始化和小学习速率来解决。但是，如果我们能够在训练过程中，能够保证非线性激活函数的输入的分布保持稳定；因此，优化函数将几乎不会陷入饱和区并且训练会加速。

\quad    \; 我们将训练过程中，一个网络内部节点的分布的改变称为$Internal$ $Covariate$ $Shift$。消除它必定将加快训练。我们提出了一个新机制：$Batch$ $Normalization$，它采取一个step去减少internal covariate shift，通过该step将显著加速深度神经网络的训练。normalization step固定层的输入的均值和方差。Batch Normalization通过减少梯度对参数scale和初始值的依赖，有利于梯度在网络内部的流动。这允许我们去使用更高的学习速率而不会有发散的风险。更进一步，BN regularizes模型并且减少了模型中dropout的必要性。最终，BN通过阻止网络陷入饱和，使得可以使用饱和非线性激活函数。

\quad    \; 在4.2节，我们应用BN到分类的state of art网络。我们只要原始steps的7% step就可以达到相同的性能，最终可以取得较大的准确率提升。使用训练好的BN之后网络的集成版本，top-5错误率超过了当前的最好结果。

2.减少内部协方差（Towards Reducing Internal Covariate Shift）

\quad    \; 我们定义$Internal$ $Covariate$ $Shift$为训练过程中网络参数变化导致的网络activation的分布的改变。为了提高训练（加速，提升效果，原文为：To improve the training），我们必须想办法去减少内部协方差。通过固定训练过程中层输入$\text{x}$的分布，我们期望去提升训练速度。模型的输入被白化能加速模型训练过程中的收敛速度。例如，通过线性变换将activations变换到0均值、1方差并且去相关。因为每一层的输入都来自前一层，所以对每一层的输入进行白化将会十分有益处。通过白化每一层的输入，我们将采取一个step去固定输入的分布，它将消除$internal$ $covariate$ $shift$带来的不利影响。

\quad    \; 我们可以考虑在训练过程中的每一个step或间隔一些step白化activations。白化方法：1.直接修改网络参数；2.根据网络的activations修改优化算法的参数。但是，如果这些修改被分散到所有优化step，那么，梯度下降step需要在更新参数前更新normalization，这讲降低梯度下降的效果（then the gradient descent step may attempt to update the parameters in a way that requires the normalization to be updated, which reduces the effect of the gradient step）。例如，考虑一个输入为$u$，偏差为$b$的层，然后normalizes该层的输出by减去整个数据集($\chi$)上的activation的mean：$\hat{x}=x-E[x]$，这里$x=u+b$，$\chi =\{x_{1...N}\}$代表整个训练集，$E[x]=\frac{1}{N}{\sum }_{i=1}^N{x}_i$。如果一个梯度下降step忽略$E[x]$依赖于$b$，那么它会这么更新$b$：$b\leftarrow b+\Delta b$，这里$\Delta b\propto \partial l/\partial \hat{x}$。然后$u+(b+\Delta b)-E[u+(b+\Delta b)]=u+b-E[u+b]$。因此，$b$的更新和normalization的结合导致该层的输出不变，当然loss也不会变化。在loss不变的情况下，随着训练的继续，$b$将趋向于无限。如果normalization不仅center，而且scale activations，这个问题会进一步变得严重。在最初的实验中，我们已经观察到这个现象。试验中，当normalization参数在gradient descent step之外完成时，模型blows up（参数趋向于无穷）。

\quad    \; 上面方法的问题是梯度下降优化没有把normalization takes place（N的作用）考虑在内。为了解决这个问题，我们将确保：对于任何参数，网络总是产生分布的activations。通过产生期望的分布，将允许模型关于参数的梯度（梯度依赖于模型参数$\Theta$）把normalization考虑在内。再次记向量$x$为一层的输入，$\chi$为整个数据集上输入$x$的集合。normalization然后可以被写为一个转换：$$\hat{x}=\text{Norm}(x,\chi )$$ $\hat{x}$依赖于给的训练example $x$ 和所有的example $\chi$。如果$x$由另一层产生，则$\chi$依赖于该层的参数。为了反向传播，我们将需要去计算Jacobian矩阵：$$\frac{\partial \text{Norm}(x,\chi )}{\partial x}and\frac{\partial \text{Norm}(x,\chi )}{\partial \chi }$$忽略后者将导致上述的爆炸（参数趋向于无穷）。在这个框架下，白化层输入的代价是巨大的，因为它需要计算协方差矩阵（covariance matrix）$$\text{Cov}[x]={\text{E}}_{x\in \chi }[x{x}^T]-\text{E}[x]\text{[}E{]}^T$$和inverse square root，从而去计算白化后的activations:$\text{Cov}[x{]}^{-1/2}(x-\text{E}[x])$和normalization过程的反向传播。这激励我们去寻找一种可微分并且在每次参数更新后不需要对整个数据上的activation进行分析的normalization技术作为替代方案。

\quad    \; 已经有人基于单个training example或者图像给定区域的不同feature map的统计来白化。但是这种通过丢弃activations的absolute scale的方法会改变模型的表示能力。我们想要在网络中保留absolute scale信息，通过normalizing the activations in a training example relative to the statistics of the entire training data.

3.基于Mini-Batch的统计实现Normalization（Normalization via Mini-Batch Statistics）

\quad    \; 因为白化所有层的输入是昂贵的并且不是处处可微的，所以我们做了两个两个简化：第一个是不再同时白化 层输入、输出节点，我们将normalize each scalar feature independently, by making it have the mean of zero and the variance of 1。对于一个$d$维输入的层（记输入为$x=(x^{(1)...x^d})$ ），我们将normalize每一维：$${\hat{x}}^{(k)}=\frac{x^{(k)}-\text{E}[x^{(k)}]}{\sqrt{\text{Var}[x^{(k)}]}}$$这里的期望$\text{E}$和方差$\text{Var}$是在整个训练集上计算的。正如LeNet-5中所说，这样的normalization加速了收敛，即使是features没有被去相关。

注意：简单的normalize一层的每一个输入可能改变该层的表示能力。例如，normalizing the inputs of a sigmoid would constrain them to the linear regime of the nonlinearity。为了解决normalization可能将激活函数限制到线性区，从而减少非线性能力的问题，我们确保：$the$ $transformation$ $inserted$ $in$ $the$ $network$ $can$ $represent$ $the$ $identity$ $tranform$。为了实现这个，我们给每个activation $x^{(k)}$ 引入一对参数${\gamma }^{(k)}$, ${\beta }^{(k)}$，来缩放(scale)和平移(shift) the normalized value：$$y^{(k)}={\gamma }^{(k)}{\hat{x}}^{(k)}+{\beta }^{(k)}$$引入的两个参数和原始模型的参数一样，通过学习获得（训练过程中顺便就学习了新加的两个参数，并不需要单独学习），这两个参数的引入恢复了网络的表示能力。事实上，通过设置${\gamma }^{(k)}=\sqrt{\text{Var}[x^{(k)}]}$ ，${\beta }^{(k)}=\text{E}[x^{(k)}]$，我们能得到原始的activations，如果这是最应该做的事。

\quad    \; 在batch配置下，每一个训练step是基于整个训练集的，我们将使用整个集去normalize activations。但是，当使用随机优化时，这是不切实际的。因此，我们做出第二个简化：因为我们使用min-batches在随机梯度训练中，每一个mini-batch produces estimates of the mean and variance of each activation。为了normalization使用的statistics能够完全参与梯度的反向传播。注意：the use of mini-batches is enabled by computation of per-dimension variances rather than joint covariances；在joint情况下，将需要regularization，因为mini-batch size很可能比activation的数目要小，导致奇异covariance矩阵。

\quad    \; 考虑一个大小为$m$的mini-batch。因为normalization被独立应用到每一个activation（标量形式的normalization），让我们关注一个activation $x^{(k)}$并且为了清晰，省略掉$k$。在mini-batch activations有$m$个值，
$$\mathcal{B}=\{x_{1...m}\}$$令normalized后的值记为${\hat{x}}_{1...m}$，同时，它们的线性变换后的值记为$y_{1...m}$。我们把这个变换$${\text{BN}}_{\gamma ,\beta }:x_{1...m}\to y_{1...m}$$记为$Batch$ $Normalization$ $Tranform$。在算法1中详细说明了BN。在该算法中，$ϵ$是一个为了数值稳定性而加到mini-batch variance上的常数。

\quad    \; BN变换能够被添加到网络中去操纵任何activation。在公式$y={\text{BN}}_{\gamma ,\beta }(x)$中，我们指出了参数$\gamma$和$\beta$是被学习的，但是应该注意到：BN转换不是独立处理每一个训练example的activation。确切的说（Rather），${\text{BN}}_{\gamma ,\beta }(x)$依赖于training example和mini-batch中的其它example。scaled and shifted后的值$y$被传到网络的其它层。normalized activations $\hat{x}$处于我们的变换内部，但是它的存在是很重要的。只要每一个mini-batch的元素是从相同的分布中采样得到，并且我们忽略$ϵ$，那么任何$\hat{x}$的值的分布的期望值为0，variance为1。这能够通过${\sum }_{i=1}^m{\hat{x}}_i=0$和${\sum }_{i=1}^m{\hat{x}}_i^2=1$得到验证，并且得到预测效果。每一个normalized activation ${\hat{x}}^{(k)}$能够被看做一个sub-network（composed of the linear transform $y^{(k)}={\gamma }^{(k)}{\hat{x}}^{(k)}+{\beta }^{(k)}$, followed by other process done by the original netwoork）的输入。这些sub-network的输入都有固定的mean和variances，并且尽管这些normalized ${\hat{x}}^{(k)}$的 joint 分布在训练中能够改变，我们期待normalization on inputs的引入加速sub-network及整个network的训练。

\quad    \; 在训练中，我们需要去让梯度反向传播通过这个变换，同时计算loss关于BN transform中参数的梯度。我们使用链式法则(简化之前)

$\frac{\partial l}{\partial {\hat{x}}_i}=\frac{\partial l}{\partial y_i}\cdot \gamma$

$\frac{\partial l}{\partial {\sigma }_{\mathcal{B}}^2}={\sum }_{i=1}^m\frac{\partial l}{\partial {\hat{x}}_i}\cdot (x_i-{\mu }_{\mathcal{B}})\cdot \frac{-1}{2}({\sigma }_{\mathcal{B}}^2+ϵ{)}^{-3/2}$

$\frac{\partial l}{\partial {\mu }_{\mathcal{B}}^2}=\left({\sum }_{i=1}^m\frac{\partial l}{\partial {\hat{x}}_i}\cdot \frac{-1}{\sqrt{{\sigma }_{\mathcal{B}}^2+ϵ}}\right)+\frac{\partial l}{\partial {\sigma }_{\mathcal{B}}^2}\cdot \frac{{\sum }_{i=1}^m-2(x_i-{\mu }_{\mathcal{B}})}{m}$

$\frac{\partial l}{\partial x_i}=\frac{\partial l}{\partial {\hat{x}}_i}\cdot \frac{1}{\sqrt{{\sigma }_{\mathcal{B}}^2+ϵ}}+\frac{\partial l}{\partial {\sigma }_{\mathcal{B}}^2}\cdot \frac{2(x_i-{\mu }_{\mathcal{B}})}{m}+\frac{\partial l}{\partial {\mu }_{\mathcal{B}}}\cdot \frac{1}{m}$

$\frac{\partial l}{\partial \gamma }={\sum }_{i=1}^m\frac{\partial l}{\partial y_i}\cdot {\hat{x}}_i$

$\frac{\partial l}{\partial \beta }={\sum }_{i=1}^m\frac{\partial l}{\partial y_i}$

\quad    \; 因此，BN变换是一个可微分变换，它引入normalized activations到网络中。这确保随着模型的训练，层能够持续学习输入的分布，内部协方差不断变小，因此加速训练。因此，学习到的仿射变换被应用到这些normalized activation将允许BN变换去表示identity变换并且保存网络的容量。

3.1.Training and Inference with Batch-Normalized Networks

\quad    \; 为了BN一个网络，根据算法1，我们选择一个sub-network，并且在内部插入BN变换。任何把$x$当做输入的层，现在把$\text{BN}(x)$当做输入。一个使用$Batch$ $Normalization$的模型能够使用batch gradient descent或者stochastic gradient descent with a mini-batch size $m$>1训练，或者使用其它变种，例如Adagrad。activations的normalization依赖于mini-batch，这使得训练更加高效，但在推理中，不是必要，也不是想要的。我们希望输出只依赖于input。对于这个问题，一旦网络被训练，我们使用的normaliztion：
$$\hat{x}=\frac{x-\text{E}[x]}{\sqrt{\text{Var}[x]+ϵ}}$$
using population而不是mini-batch上的统计统计值。忽略$ϵ$，这些normalized activations在训练过程中都有mean 0，variance 1。我们使用variance的无偏估计 $\text{Var}=\frac{m}{m-1}\cdot {\text{E}}_{\mathcal{B}}[{\sigma }_{\mathcal{B}}^2]$，这里期望$\text{E}$是在大小为$m$的训练mini-batch上计算得到的，${\sigma }_{\mathcal{B}}^2$采样得到的mini-batch上的variances。使用moving averages，我们能够在训练过程中追踪一个模型的准确率。因为在inference中，means和variances是固定的，normalization就是被应用到每一个activation上的一个线性变换。它进一步能被分解为scaling by $\gamma$和shift by $\beta$，从而产生一个线性变换替代$\text{BN}(x)$。算法2总结了训练Batch Normalized网络的步骤。

3.2.Batch-Normalized Convolutional Networks

\quad    \; BN能够被应用到网络中的任意activations集上。这里，我们聚焦一个包含一个仿射变换加（followed）一个element-wise激活函数的变换：$$\text{z}=g(W\text{u}+b)$$这里$W$和$b$是模型学习到的参数，$g(\cdot )$是激活函数，例如sigmoid、ReLU。这个公式同时适用于FC层和conv层。我们在激活函数前加BN来normalize仿射变换的输出$\text{x}=W\text{u}+b$。我们也可以对放射变换的输入$\text{u}$进行normalization，因为$\text{u}$很有可能是另一个非线性激活函数的输出，训练过程中，它的分布很有可能发生改变；同时，限制第一第二moments将不能消除covariate shift。相反，$W\text{u}+b$更可能有一个对称的，非稀疏的分布，that is “more Gaussian”；normalize $W\text{u}+b$将产生一个稳定的分布。

注意，我们normalize $W\text{u}+b$后，偏差$b$能够被忽略因为它的效用将被$\beta$（算法1）替代。因此，$\text{z}=g(W\text{u}+b)$被下面的公式替代：$$\text{z}=g(\text{BN}(W\text{u}))$$这里BN变换被独立应用到$\text{x}=W\text{u}$的每一维，每一维都有两个参数${\gamma }^{(k)}$，${\beta }^{(k)}$。

\quad    \; 对于卷积层，我们另外想normalization去遵守convolution的特性，feature map中不同位置的不同元素以相同的方式进行normalization。为了实现这个，在一个mini-batch，我们对一个mini-batch中所有位置的activation进行joint normalization。在算法1，我们令$\mathcal{B}$是所有feature maps中的一个feature map over mini-batch，所以在大小为$m$的mini-batch上，算法1中的m将变为$m^{\prime }=|\mathcal{B}|=m\cdot pq$。我们学习一对参数${\gamma }^{(k)}$和${\beta }^{(k)}$ per feature map而不是per activation。算法2进行相似的修改，所以在一个给定的feature map中，BN变换应用到线性变换to每一个activation。

3.3.Batch-Normalized enables higher learning rates

\quad    \; 在传统的深度网络中，过高的学习速率可能导致梯度爆炸或消失，同时陷入糟糕的局部最优。Batch Normalization帮助解决这个问题。通过normalize整个网络的activations，它防止了参数的微小变化在网络中的放大和梯度效果的降低。例如，它阻止了训练陷入非线性激活函数的饱和区。

\quad    \; Batch Normalization同时使得训练过程对参数scale的适应性更好。一般情况下，大的学习速率可能增加层的参数的scale，这使得反向传播过程中梯度的scale的增加并且导致模型爆炸。但是，使用BN，层的参数的scale不会影响该层的反向传播。事实上，对于一个标量$a$:$$\text{BN}(W\text{u})=\text{BN}((aW)\text{u})$$并且我们展示下对应的反向传播过程：$$\frac{\partial \text{BN}((aw)\text{u})}{\partial \text{u}}=\frac{\partial \text{BN}(W\text{u})}{\partial \text{u}}$$ $$\frac{\partial \text{BN}((aw)\text{u})}{\partial \text{u}}=\frac{1}{a}\cdot \frac{\partial \text{BN}(W\text{u})}{\partial W}$$通过上式可以看出，scale不影响层的Jacobian矩阵，进而也不影响梯度的反向传播。更进一步，越大的权重导致越小的梯度，并且BN将稳定参数的增长。

\quad    \; 我们进一步推测BN可能导致Jacobian矩阵有单个值接近1。这是有益于训练的。考虑输入都进行了normalization的两连续层，normalized的输入向量之间的变换记为：$\hat{\text{z}}=F(\hat{\text{x}})$。如果我们假设$\hat{\text{x}}$和$\hat{\text{z}}$是高斯分布并且不相关，$F(\hat{\text{x}})\approx J\hat{\text{x}}$是基于给定模型参数的一个线性变换，然后，$\hat{\text{x}}$和$\hat{\text{z}}$都有单位协方差（covariances），$I=\text{Cov}[\hat{\text{z}}]=J\text{Cov}[\hat{\text{x}}]J^T=J{J}^T$。然后$J{J}^T=I$，所以$J$中各个元素都等于1，它保存了反向传播中梯度的幅值。在现实中，变换不是线性的，并且normalized后的值不保证一定为高斯变换和独立的。但是我们依然（nevertheless）期待BN有助于梯度的传播。BN在梯度传播的准确效果仍然是一个需要进一步研究的领域。

3.4.Batch-Normalization regularizes the model

\quad    \; 当对BN网络进行训练时，单个训练example is seen in conjunction with other examples in the mini-batch，并且网络不再产生决定性的值for单个训练example。在我们的实验中，我们发现这个效应是有利于模型的泛华的。尽管在BN了的网络中一般用Dropout去减轻过拟合，但是我们发现它能够被去掉或者减少使用的次数。

4. 实验

4.1 Activations over time

\quad    \; 上图是作者在MMIST上，实现的3层FC，每层有100个activation，激活函数使用的是sigmoid，权重被初始化为很小的高斯分布的随机数。最后一层接linear+softmax层来分类。训练50000 step，mini-batch大小为60。

\quad    \; 图1a 展示了模型的准确率的变化，BN后的网络准确率更高；图1b、c展示了activation随训练step的变化。从b、c中可以看出，原始网络的activation的分布（mean和variance）随着时间变化很大，这会妨碍网络的训练。相反，BN后的网络的activation的分布在训练过程中更加稳定，这有助于训练。

4.2 ImageNet classification

\quad    \; Inception v2是在Inception v1的基础上改进得到的。主要改进有：1.增加了BN；2.将Inception模块中的5x5卷积分解为了两个3x3卷积with up to 128 filters。改进后的网络的参数量为$13.6\cdot 10^6$，去掉了FC层。训练算法使用的是SGD with momentum，mini-batch大小为32.网络的挑选依据是验证集上的validation accuracy，验证过程每张图片只取一个crop。

4.3 Accelerating BN Network

\quad    \; 简单增加BN无法充分体现我们的方法的优点。所以，作者进一步改变了训练过程中的参数：

Increase learning rate
Remove Dropout
Reduce the L2 weight regularization
Accelerate the learning rate decay
Remove Local Response Normalization，作者发现LRN是不必要的
Shuffle training examples more thoroughly主要是阻止同样的example出现在一个mini-batch内
Reduce the photometric distortions

4.4 Single-Network Classification

\quad    \; 作者对网络做了诸多修改，然后基于ILSVRC 2012数据进行了研究。


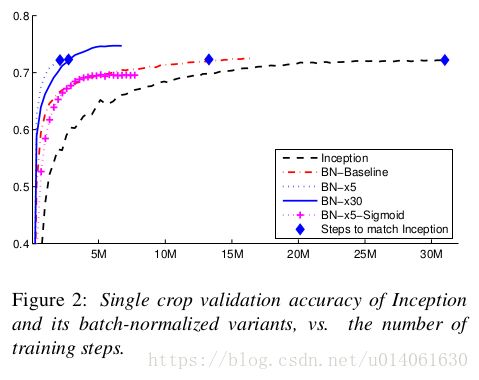
上图是各个模型的对比情况：
Inception：Inception v1，初始学习速率为0.0015
BN-Baseline：Inception的激活函数前加BN
BN-x5：在BN-Baseline基础上，将初始学习速率增大5倍：0.0075
BN-x30：在BN-x5基础上，将初始学习速率从Inception的0.0015增大30倍：0.045
BN-x5-sigmoid：在BN-x5基础上，将ReLU激活函数改为sigmoid

BN在TensorFlow中的实现

#Tensorflow中BN一般常用的API有4个：
'''
BN1 = keras.layers.BatchNormalization(
    axis,
    momentum,
    epsilon,
    center=bool,
    scale=bool)
BN2 = tf.layers.BatchNormalization(
    axis,
    momentum,
    epsilon,
    center=bool,
    scale=bool)
BN3 = tf.layers.batch_normalization(
    inputs,
    axis=-1,
    momentum=0.99,
    epsilon=0.001,
    centor=True,
    scale=True)
BN4 = tf.nn.batch_normalization(
    x,
    mean,
    variance,
    offset,
    scale,
    variance_epsilon,
    name)
'''
#tf.keras.layers.BatchNormalization
x = tf.placeholder(tf.float32,[None,224,224,3])
y = keras.layers.BatchNormalization()(x)

#tf.layers.batch_normalization
#tf.layers.BatchNormalization
x = tf.placeholder(tf.float32,[None,224,224,3])
y = tf.layers.batch_normalization(x)
y = tf.layers.BatchNormalization()(x)

#下面的tf.nn.batch_normalization基本就是BN的源码实现。具体的计算逻辑已经十分清晰
#下面的代码基本就是文中算法2的实现过程
#tf.nn.batch_normalization
x = tf.placeholder(tf.float32,[None,224,224,3])
from tensorflow.python.training import moving_averages
mode = 'train'
_extra_train_ops = []
params_shape = [x.get_shape()[-1]]
beta = tf.get_variable('beta', params_shape, tf.float32,
    initializer=tf.constant_initializer(0.0, tf.float32))
gamma = tf.get_variable('gamma', params_shape, tf.float32,
    initializer=tf.constant_initializer(1.0, tf.float32))
if mode == 'train':
  mean, variance = tf.nn.moments(x, [0, 1, 2], name='moments')

  moving_mean = tf.get_variable('moving_mean', params_shape, tf.float32,
      initializer=tf.constant_initializer(0.0, tf.float32), trainable=False)
  moving_variance = tf.get_variable('moving_variance', params_shape, tf.float32,
      initializer=tf.constant_initializer(1.0, tf.float32), trainable=False)

  _extra_train_ops.append(moving_averages.assign_moving_average(
      moving_mean, mean, 0.9))
  _extra_train_ops.append(moving_averages.assign_moving_average(
      moving_variance, variance, 0.9))
else:
  mean = tf.get_variable('moving_mean', params_shape, tf.float32,
      initializer=tf.constant_initializer(0.0, tf.float32), trainable=False)
  variance = tf.get_variable('moving_variance', params_shape, tf.float32,
      initializer=tf.constant_initializer(1.0, tf.float32), trainable=False)
  tf.summary.histogram(mean.op.name, mean)
  tf.summary.histogram(variance.op.name, variance)
y = tf.nn.batch_normalization(x, mean, variance, beta, gamma, 0.001) # 这句对应文中算法1的//normalize和//scale and shift两行。

上面我们研究了几种BN的实现，从高层API到底层API，高层API简洁，十分适合快速搭建网络，底层API十分适合研究。

附录：

Inception v2使用的模型是Inception v1的变种
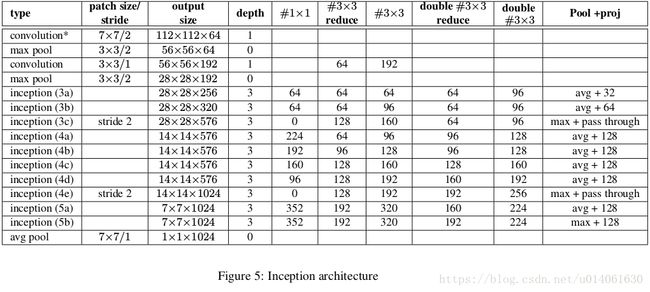
图5说明了Inception v2相对于Inception v1：GoogLLeNet的改变。主要的改变如下：

• 5x5卷积层被两个串联的3x3卷积层替代。这最多增加了9 weight layer。同时，它增加了25%的参数量，增加了30%的计算量。

• 28x28 Inception模块的数量从2个增加到3个。

• 在I模块内部，有时使用average-pooling，有时使用maximum-pooling。这在图5中有详细说明。

• 在Inception模组之间没有board pooling。但是在模组输出之前的Inception模块中使用stride 2。

我们的模型在第一个卷积层使用了separable convolution with depth multiplier 8。这减少了计算量，然而增加了训练时的内存消耗量。

Inception v2的TensorFlow实现

和Inception v1一样，首先实现Inception模块

#coding:utf-8
'''
Inception module
'''

import tensorflow as tf


def inception(inputs, 
              sub_chs,
              stride, 
              pool_mode, 
              is_training,
              scope='inception'):
  '''
  sub_chs: sub channels
  '''
  [sub_ch1, sub_ch2, sub_ch3] = sub_chs
  sub_ch4 = pool_mode[1]
  sub = []
  with tf.variable_scope(scope):
    x = inputs
    if sub_ch1:
      sub1 = tf.layers.Conv2D(sub_ch1, [1,1], stride, padding='SAME')(x)
      sub1 = tf.layers.BatchNormalization()(sub1, training=is_training)
      sub1 = tf.nn.relu(sub1)
      sub.append(sub1)
    
    sub2 = tf.layers.Conv2D(sub_ch2[0], [1,1], padding='SAME')(x)
    sub2 = tf.layers.BatchNormalization()(sub2, training=is_training)
    sub2 = tf.nn.relu(sub2)
    sub2 = tf.layers.Conv2D(sub_ch2[1], [3,3], stride, padding='SAME')(sub2)
    sub2 = tf.layers.BatchNormalization()(sub2, training=is_training)
    sub2 = tf.nn.relu(sub2)
    sub.append(sub2)
    
    sub3 = tf.layers.Conv2D(sub_ch3[0], [1,1], padding='SAME')(x)
    sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
    sub3 = tf.nn.relu(sub3)
    sub3 = tf.layers.Conv2D(sub_ch3[1], [3,3], padding='SAME')(sub3)
    sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
    sub3 = tf.nn.relu(sub3)
    sub3 = tf.layers.Conv2D(sub_ch3[1], [3,3], stride, padding='SAME')(sub3)
    sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
    sub3 = tf.nn.relu(sub3)
    sub.append(sub3)
    
    if pool_mode[1] is None:
      if pool_mode[0] == 'max':
        sub4 = tf.layers.MaxPooling2D([3,3], stride, padding='SAME')(x)
      elif pool_mode[0] == 'avg':
        sub4 = tf.layers.AveragePooling2D([3,3], stride, padding='SAME')(x)
    else:
      if pool_mode[0] == 'max':
        sub4 = tf.layers.MaxPooling2D([3,3], 1, padding='SAME')(x)
      elif pool_mode[0] == 'avg':
        sub4 = tf.layers.AveragePooling2D([3,3], 1, padding='SAME')(x)
      sub4 = tf.layers.Conv2D(sub_ch4, [1,1], stride, padding='SAME')(sub4)
      sub4 = tf.layers.BatchNormalization()(sub4, training=is_training)
      sub4 = tf.nn.relu(sub4)
    sub.append(sub4)
    
    x = tf.concat(sub, axis=-1)
  return x


if __name__ == '__main__':
  x = tf.placeholder(tf.float32, [192, 28, 28, 3])
  y1 = inception(x, [64, [96,128], [16,32]], 2, ['max',32], is_training=True, scope='1')
  assert y1.get_shape().as_list()==[192,14,14,256]
  y2 = inception(x, [64, [96,128], [16,32]], 2, ['max',None], is_training=True, scope='2')
  print('inception is ok')

实现了Inception模块，下面，我们对Inception v1进行修改，构建Inception v2。

#coding:utf-8
'''
Inception v1
'''

import tensorflow as tf
relu = tf.nn.relu
import inception_v2_module as modules

def print_activation(x):
  print(x.op.name, x.get_shape().as_list())

def inference(inputs,
              num_classes=10,
              is_training=True,
              dropout_rate=0.4):
  '''
  inputs: a tensor of images
  num_classes: the num of category.
  is_training: set ture when it used for training
  dropout_prob: the rate of dropout during training
  '''
  x = tf.placeholder(tf.float32, [None,224,224,3])
  caches = []
  x = inputs
  print_activation(x)
  # conv1
  x = tf.layers.Conv2D(64, [7,7], 2, padding='SAME', name='conv1')(x)
  print_activation(x)
  # bn1
  x = tf.layers.BatchNormalization(name='bn1')(x, training=is_training)
  print_activation(x)
  # relu1
  x = tf.nn.relu(x,name='relu1')
  print_activation(x)
  # pool1
  x = tf.layers.MaxPooling2D([3,3], 2, padding='SAME', name='pool1')(x)
  print_activation(x)
  # conv2
  x = tf.layers.Conv2D(64, [1,1], 1, padding='SAME', name='conv2')(x)
  print_activation(x)
  # bn2
  x = tf.layers.BatchNormalization(name='bn2')(x, training=is_training)
  print_activation(x)
  # relu1
  x = tf.nn.relu(x,name='relu2')
  print_activation(x)
  # conv3
  x = tf.layers.Conv2D(192, [3,3], 1, padding='SAME', name='conv3')(x)
  print_activation(x)
  # bn3
  x = tf.layers.BatchNormalization(name='bn3')(x, training=is_training)
  print_activation(x)
  # relu3
  x = tf.nn.relu(x,name='relu3')
  print_activation(x)
  # pool3
  x = tf.layers.MaxPooling2D([3,3], 2, padding='SAME', name='pool3')(x)
  print_activation(x)
  with tf.variable_scope('inception3'):
    # inception_3a
    x = modules.inception(x, [64, [64,64], [64,96]], 1, ['avg',32], is_training=True, scope='inception_3a')
    print_activation(x)
    # inception_3b
    x = modules.inception(x, [64, [64,96], [64,96]], 1, ['avg',64], is_training=True, scope='inception_3b')
    print_activation(x)
    # inception_3c
    x = modules.inception(x, [0, [128,160], [64,96]], 2, ['max',None], is_training=True, scope='inception_3c')
    print_activation(x)
  with tf.variable_scope('inception4'):
    # inception_4a
    x = modules.inception(x, [224, [64,96], [96,128]], 1, ['avg',128], is_training=True, scope='inception_4a')
    caches.append(x)
    print_activation(x)
    # inception_4b
    x = modules.inception(x, [192, [96,128], [96,128]], 1, ['avg',128], is_training=True, scope='inception_4b')
    print_activation(x)
    # inception_4c
    x = modules.inception(x, [160, [128,160], [128,160]], 1,['avg',128], is_training=True, scope='inception_4c')
    print_activation(x)
    # inception_4d
    x = modules.inception(x, [96, [128,192], [160,192]], 1, ['avg',128], is_training=True, scope='inception_4d')
    print_activation(x)
    caches.append(x)
    # inception_4e
    x = modules.inception(x, [0, [128,192], [192,256]], 2, ['max',None], is_training=True, scope='inception_4e')
    print_activation(x)
  with tf.variable_scope('inception5'):
  # inception_5a
    x = modules.inception(x, [352, [192,320], [160,224]], 1, ['avg',128], is_training=True, scope='inception_5a')
    print_activation(x)
    # inception_5b
    x = modules.inception(x, [352, [192,320], [192,224]], 1, ['max',128], is_training=True, scope='inception_5b')
    print_activation(x)
  # avg_pool
  _ksize = x.get_shape().as_list()[1]
  x = tf.layers.AveragePooling2D([_ksize,_ksize], 1, name='avg_pool')(x)
  print_activation(x)
  # dropout
  x = tf.layers.Dropout(dropout_rate, name='dropout')(x)
  print_activation(x)
  # linear+softmax
  logits = tf.layers.Conv2D(num_classes, [1,1], 1, 
                            activation=tf.nn.softmax, name='linear-softmax')(x)
  print_activation(logits)
  return logits, caches

def build_cost(logits, labels, scope='costs'):
  with tf.variable_scope(scope):
    cost = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
        logits=logits, labels=labels), name='xent')
  return cost

def build_sub_cost(cache, labels, scope='sub_costs'):
  num_classes = labels.get_shape().as_list()[-1]
  with tf.variable_scope(scope):
    x = cache
    x = tf.layers.AveragePooling2D([5,5], 3, name='avg_pool')(x)
    x = tf.layers.Conv2D(128, [1,1], 1, activation=relu, name='conv')(x)
    _ksize = x.get_shape().as_list()[1]
    x = tf.layers.Conv2D(1024, [_ksize,_ksize], 1, activation=relu, name='fc')(x)
    x = tf.layers.Dropout(0.7)(x)
    logits = tf.layers.Conv2D(num_classes, [1,1], 1, activation=tf.nn.softmax, name='fc-softmax')(x)
    cost = build_cost(tf.layers.flatten(logits), labels)
  return cost

def build_train_op(cost, lrn_rate=0.001, scope='train'):
  with tf.variable_scope(scope):
    update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS) # for BN
    with tf.control_dependencies(update_ops):
      train_op = tf.train.AdamOptimizer(lrn_rate).minimize(cost)
  return train_op


if __name__ == '__main__':
  mode = 'train'
  with tf.variable_scope('inputs'):
    images = tf.placeholder(tf.float32, [None,224,224,3])
    labels = tf.placeholder(tf.float32, [None, 1000])
  
  logits, caches = inference(inputs=images, num_classes=1000)
  logits = tf.layers.flatten(logits)
  print('inference is ok!')
  if mode=='train':
    with tf.variable_scope('costs'):
      cost = tf.add_n([build_cost(logits, labels),
                       build_sub_cost(caches[0], labels, scope='sub_cost1'),
                       build_sub_cost(caches[1], labels, scope='sub_cost2')])
  else:
    cost = build_cost(logits, labels)
  print('build_cost is ok!')
  train_op = build_train_op(cost, lrn_rate=0.001)
  print('build_train_op is ok!')
  
  sess = tf.Session()
  tf.summary.FileWriter('./',sess.graph)

任何转载，都请注明引用。

对于代码的使用必须声明

---

2 Shimodaira, Hidetoshi. Improving predictive inference under covariate shift by weighting the log-likelihood function. Journal of Statistical Planning and Inference, 90(2):227–244, October 2000.