动手学深度学习（四十一）——深度循环神经网络（Deep-RNN）

  本节非常简单，就是在RNN的基础上加了层的概念，毕竟之前讨论的RNN、GRU和LSTM我们都是在单层神经网络的基础上讨论的

一、深度循环神经网络

  到目前为止，我们只讨论了具有一个单向隐藏层的循环神经网络。其中，隐变量和观测值与具体的函数形式的交互方式是相当随意的。只要我们可以对不同的交互类型建模具有足够的灵活性，这就不是一个大问题。然而，对于一个单层来说，这可能具有相当的挑战性。在线性模型的情况下，我们通过添加更多的层来解决这个问题。而在循环神经网络中，因为我们首先需要决定如何添加以及在哪里添加额外的非线性，因此这个问题有点棘手。

  事实上，我们可以将多层循环神经网络堆叠在一起，通过对几个简单层的组合，产生了一个灵活的机制。特别是，数据可能与不同层的堆叠有关。例如，我们可能希望保持有关金融市场状况（熊市或牛市）的高层数据可用，而在底层数据就只记录较短期的时间动态。

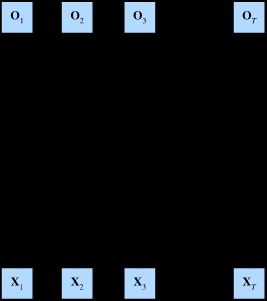
  下面是具有 $L$ 个隐藏层的深度循环神经网络，每个隐藏状态都连续地传递到当前层的下一个时间步和下一层的当前时间步。(有趣的地方在于你将之前的RNN图片与之对比，可以发现$H_1^{(1)}、H_2^{(1)}$他们是之前对应的输出，现在只是变成了下一层神经元的输入)

二、函数依赖关系

  我们可以对深度架构中的函数依赖关系形式化，这个架构是由$L$ 个隐藏层构成。假设我们在时间步 $t$ 有一个小批量的输入数据 ${\mathbf{X}}_t\in {\mathbb{R}}^{n\times d}$（样本数：$n$，每个样本中的输入数：$d$）。同时，将 $l^{\mathrm{t}\mathrm{h}}$ 隐藏层（$l=1,\dots ,L$）的隐藏状态设为 ${\mathbf{H}}_t^{(l)}\in {\mathbb{R}}^{n\times h}$（隐藏单元数：$h$），输出层变量设为 ${\mathbf{O}}_t\in {\mathbb{R}}^{n\times q}$（输出数：$q$）。设置 ${\mathbf{H}}_t^{(0)}={\mathbf{X}}_t$，第 $l$ 个隐藏层的隐藏状态使用激活函数 ${\varphi }_l$ 的表示如下：

$${\mathbf{H}}_t^{(l)}={\varphi }_l({\mathbf{H}}_t^{(l-1)}{\mathbf{W}}_{xh}^{(l)}+{\mathbf{H}}_{t-1}^{(l)}{\mathbf{W}}_{hh}^{(l)}+{\mathbf{b}}_h^{(l)}),$$

  其中，权重 ${\mathbf{W}}_{xh}^{(l)}\in {\mathbb{R}}^{h\times h}$ 和 ${\mathbf{W}}_{hh}^{(l)}\in {\mathbb{R}}^{h\times h}$ 和偏置 ${\mathbf{b}}_h^{(l)}\in {\mathbb{R}}^{1\times h}$ 都是第 $l$ 个隐藏层的模型参数。最后，输出层的计算仅基于第 $l$ 个隐藏层最终的隐藏状态：

$${\mathbf{O}}_t={\mathbf{H}}_t^{(L)}{\mathbf{W}}_{hq}+{\mathbf{b}}_q,$$

其中，权重 ${\mathbf{W}}_{hq}\in {\mathbb{R}}^{h\times q}$ 和偏置 ${\mathbf{b}}_q\in {\mathbb{R}}^{1\times q}$ 都是输出层的模型参数。

  与多层感知机一样，隐藏层的数目 $L$ 和隐藏单元的数目 $h$ 都是超参数。也就是说，它们可以由我们来调整或指定。另外，用门控循环单元或长短期记忆网络的隐藏状态来代替深度RNN中的隐藏状态进行计算，可以很容易地得到深度门控循环神经网络(沐神在课程中说使用LSTM和GRU就看个人爱好了，并没有本质上的差别，当然后面还有更NB的transformer可以应用)，毕竟Attention is all you need 不是闹着玩儿的。

三、简介实现

import torch
from torch import nn
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

Downloading ../data/timemachine.txt from http://d2l-data.s3-accelerate.amazonaws.com/timemachine.txt...

3.1 网络构建

# 超参数架构决策与单层lstm中相同，需要输入和输出选择相同的数量，隐藏单元设置为256，只是多了一个隐藏层层数
vocab_size,num_hiddens,num_layers = len(vocab),256,2
num_inputs = vocab_size
device = d2l.try_gpu()
lstm_layers = nn.LSTM(num_inputs,num_hiddens,num_layers)
model = d2l.RNNModel(lstm_layers,len(vocab))
model = model.to(device)

3.2 训练与预测

num_epochs,lr=500,2
d2l.train_ch8(model,train_iter,vocab,lr,num_epochs,device)

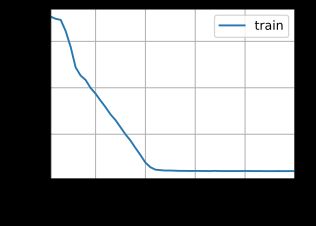
perplexity 1.0, 161938.1 tokens/sec on cuda:0
time traveller for so it will be convenient to speak of himwas e
traveller with a slight accession ofcheerfulness really thi

四、总结

• 在深度循环神经网络中，隐藏状态的信息被传递到当前层的下一时间步和下一层的当前时间步
• 有许多不同风格的深度循环神经网络，如LSTM、GRU或者经典RNN网络。这些模型在深度学习框架中都有高级的API涵盖
• 总体二言，深度RNN需要大量的工作（学习率调整、修剪）来确保合适的收敛，模型地初始化也需要非常谨慎
• 上面的两层模型在200个epoch的时候就基本收敛了，而之前单层模型在差不多300个epoch的时候才会收敛。多层增加了非线性，加速了收敛但是也增加了过拟合的风险。通常不会采用特别深的RNN网络