Swin-Transformer:Hierarchical Vision Transformer using Shifted Windows详细解读
Swin-Transformer:Hierarchical Vision Transformer using Shifted Windows
Swin Transformer是2021年微软研究院发表在ICCV上的一篇文章,并且已经获得ICCV 2021 best paper的荣誉称号。本文主要是为了记录在学习过程中遇到的一些问题,希望可以给大家带来帮助~
摘要
本文介绍了一种称为Swin Transformer的新型视觉Transformer,它可以用作计算机视觉的通用backbone
目前Transformer应用到图像领域主要有两大挑战:
(1)视觉实体变化大,在不同场景下Vision Transformer性能未必很好;(多层级)
(2)图像分辨率高,像素点多,Transformer基于全局自注意力的计算导致计算量较大。(滑窗)
针对上述两个问题,我们提出了一种包含滑窗操作,具有层级设计的Swin Transformer。
网络总体架构
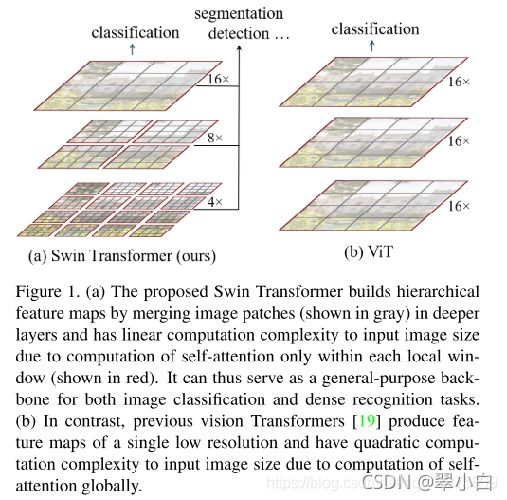
在介绍总体框架之前,先说一下文章中给出的图1,图1中左边是本文要讲的swin transformer,右图是ViT模型(https://arxiv.org/abs/2010.11929)通过观察,可以发现两点不同:
- Swin Transformer使用了类似卷积神经网络中的层次化构建方法(Hierarchical feature maps)。而在之前的Vision Transformer中是一开始就直接下采样16倍,后面的特征图也是维持这个下采样率不变。
- 在Swin Transformer中使用了Windows Multi-Head Self-Attention**(W-MSA**)的概念,相对于Vision Transformer中直接对整个特征图进行Multi-Head Self-Attention,这样做的目的是能够减少计算量的,虽然减少了计算量但也会隔绝不同窗口之间的信息传递,所以在论文中作者又提出了 Shifted Windows Multi-Head Self-Attention(SW-MSA)的概念,通过此方法能够让信息在相邻的窗口中进行传递。
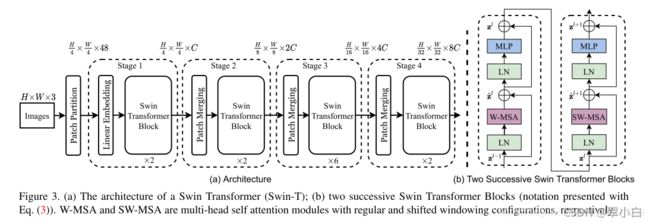
接着,看一下网络的总体架构,可以把它分为5部分:
(1)patch partition是对图片做一个划分,如果每个patch size是4,那就是对图片做一个划分,一共有224/4* 224/4个patch,每个patch的维度就是443,然后把一个个patch在通道方向拉平,也就是48,把维度展平。
(2)linear embedding层(后面接了一个层归一化)是对每个像素的channels数据做线性变换,把48映射到后续swin transformer block需要的embedding size,比如架构中把48映射为C,图像大小变为224/4×224/4×C
(3)经过2个swin transformer block,如架构中的图b,是两个encoder,transformer的编码器从来不改变他的输入输出的形状,所以经过swin transformer block形状没有发生变化。输出图片大小仍然为224/4×224/4×C
(4)之后就是patch merging做一个融合,他的作用就是缩小分辨率,增大感受野,做一个下采样,也就是说他这里有一个维度的变化,之前维度是C,转变为962,其实他在做下采样的时候是先变成C4,然后C这个维度又做了个linear,映射到为2。所以它的维度为224/4×224/4×2C,经过swin transformer block形状没有发生变化,后面的结构也一样
(5)最后对于分类网络,后面还会接上一个Layer Norm层、全局池化层以及全连接层得到最终输出。
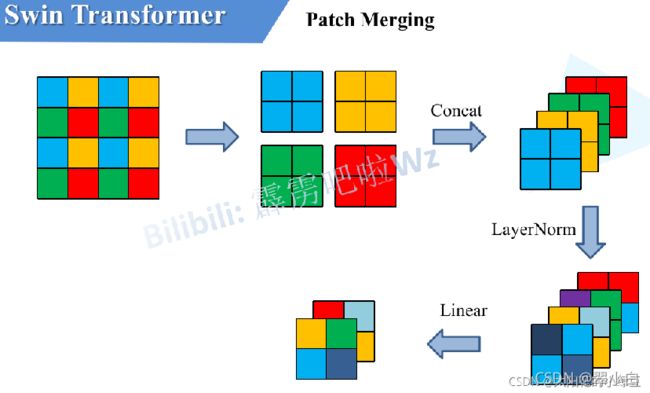
patch Merging(本模块参考的是霹雳大神的讲解)
除Stage1外,在每个Stage中首先要通过一个Patch Merging层进行下采样。如下图所示,假设输入Patch Merging的是一个4x4大小的单通道特征图(feature map),Patch Merging会将每个2x2的相邻像素划分为一个patch,然后将每个patch中相同位置(同一颜色)像素给拼在一起就得到了4个feature map。接着将这四个feature map在深度方向进行concat拼接,然后在通过一个LayerNorm层。最后通过一个全连接层在feature map的深度方向做线性变化,将feature map的深度由C变成C/2。通过这个简单的例子可以看出,通过Patch Merging层后,feature map的高和宽会减半,深度会翻倍。
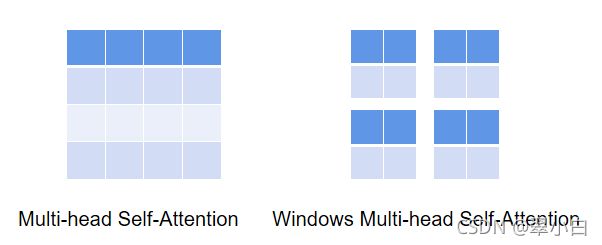
W-MSA
引入Windows Multi-head Self-Attention(W-MSA)模块是为了减少计算量。如下图所示,左侧使用的是普通的Multi-head Self-Attention(MSA)模块,对于feature map中的每个像素,在Self-Attention计算过程中需要和所有的像素去计算。但在图右侧,在使用Windows Multi-head Self-Attention(W-MSA)模块时,首先将feature map按照MxM(例子中的M=2)大小划分成一个个Windows,然后单独对每个Windows内部进行Self-Attention,这样做的目的是减少计算量,缺点是窗口之间无法进行交流。
它是如何减少计算量的呢,计算量减少了多少,论文中给出两个公式,但是并没有详细的描述公式是怎么来的,下面就让我们证明一下,公式(1)和公式(2)都是论文给出的,接下来我们来证明一下

计算注意力的公式为:
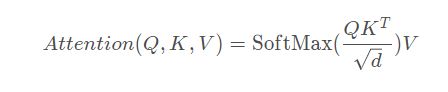
MSA计算步骤:
(1)输入x的维度为(hw,C),生成Q,K,V三个特征向量,W的维度是(C,C),那么这三项的复杂度是3hwC^2,具体如下图所示,最后得到hwC个像素,每个像素做了C次计算,得到![]()
![]()
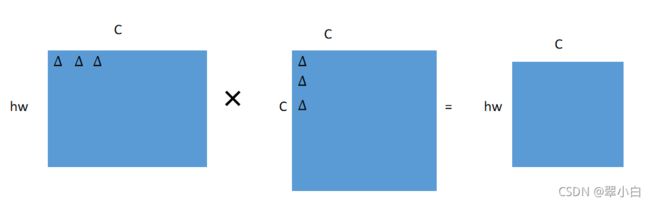
(2)![]()
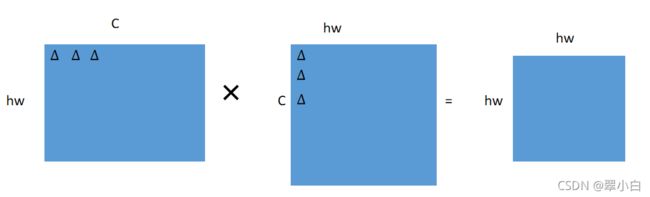
(3)![]()
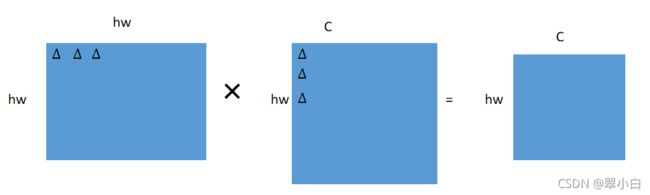
(4)![]()
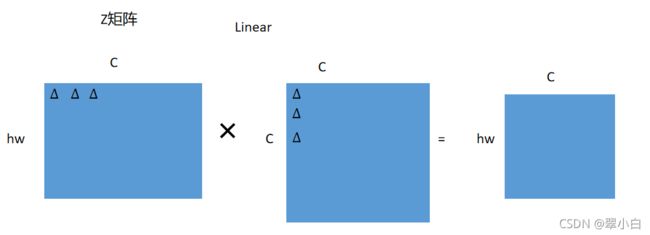
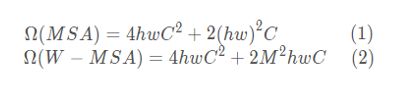
最后相加起来就是公式(1)
W-MSA的计算步骤:

SW-MSA详解
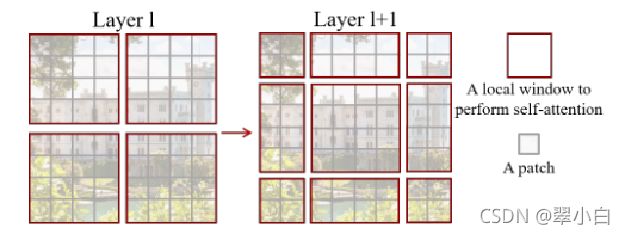
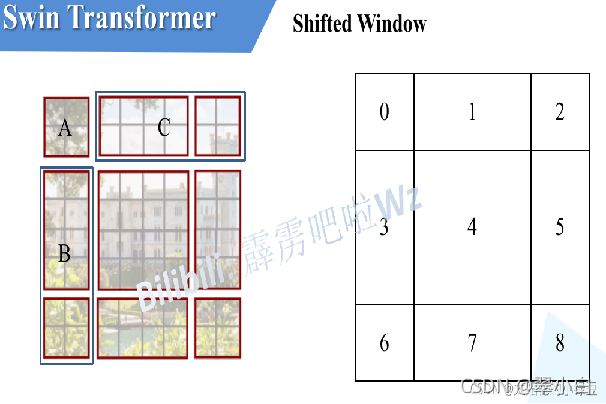
采用W-MSA模块时,只会在每个窗口内进行自注意力计算,所以窗口与窗口之间是无法进行信息传递的。为了解决这个问题,作者引入了Shifted Windows Multi-Head Self-Attention(SW-MSA)模块。如下图所示,左侧使用的是刚刚讲的W-MSA(假设是第L层),那么根据之前介绍的W-MSA和SW-MSA是成对使用的,那么第L+1层使用的就是SW-MSA(右侧图)。根据左右两幅图对比能够发现窗口(Windows)发生了偏移(可以理解成窗口从左上角分别向右侧和下方各偏移了⌊ M /2 ⌋个像素)。看下偏移后的窗口(右侧图),比如对于第一行第2列的2x4的窗口,它能够使第L层的第一排的两个窗口信息进行交流。再比如,第二行第二列的4x4的窗口,他能够使第L层的四个窗口信息进行交流,其他的同理。那么这就解决了不同窗口之间无法进行信息交流的问题。可以发现通过将窗口进行偏移后,由原来的4个窗口变成9个窗口了。后面又要对每个窗口内部进行MSA,这样做感觉又变麻烦了。为了解决这个麻烦,作者又提出而了Efficient batch computation for shifted configuration,一种更加高效的计算方法。下面是原论文给的示意图。
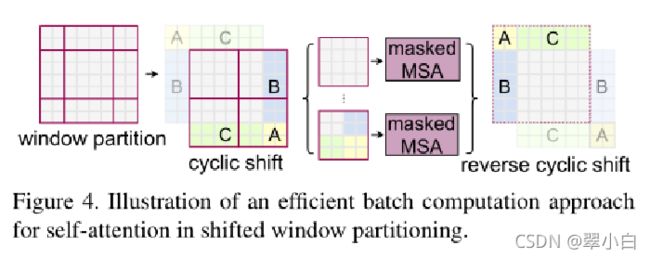
由于这个不好理解,因此找了一些材料帮助大家理解,下图左侧是刚刚通过偏移窗口后得到的新窗口,右侧是为了方便大家理解,对每个窗口加上了一个标识。然后0对应的窗口标记为区域A,3和6对应的窗口标记为区域B,1和2对应的窗口标记为区域C。之后先将区域A和C移到最下方,接着,再将区域A和B移到最右侧。
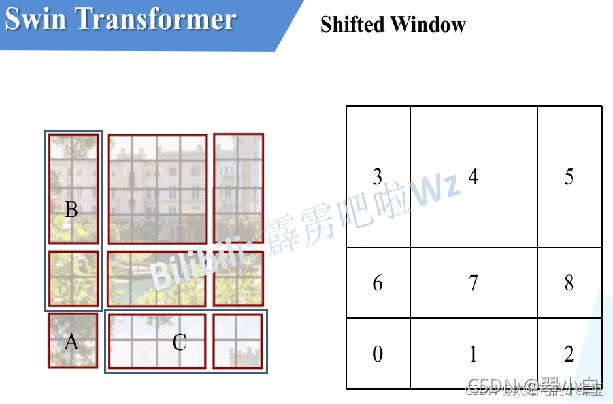
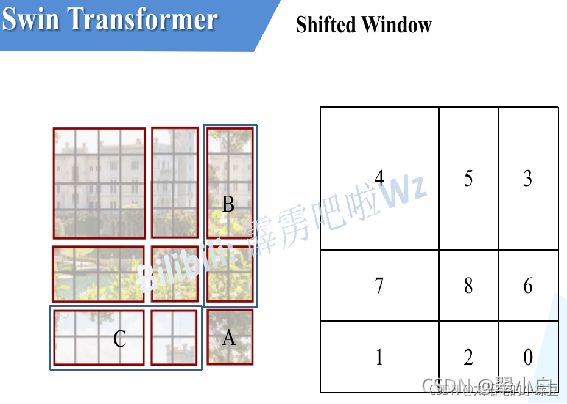
移动完后,4是一个单独的窗口;将5和3合并成一个窗口;7和1合并成一个窗口;8、6、2和0合并成一个窗口。这样又和原来一样是4个4x4的窗口了,所以能够保证计算量是一样的。但是把不同的区域合并在一起(比如5和3)进行MSA,这信息不就乱了吗?为了防止这个问题,在实际计算中使用的是masked MSA即带mask的MSA,这样就能够通过设置mask来隔绝不同区域的信息了。
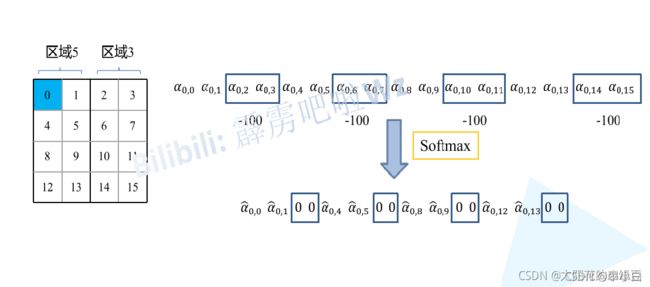
对于该窗口内的每一个像素(或称token,patch)在进行MSA计算时,都要先生成对应的query(q),key(k),value(v)。假设对于上图的像素0而言,得到q0后要与每一个像素的k进行匹配(match),假设α 0,0 代表q 0 与像素0对应的k^0进行匹配的结果,那么同理可以得到α 0,0 至α 0 , 15。按照普通的MSA计算,接下来就是SoftMax操作了。但对于这里的masked MSA,像素0是属于区域5的,我们只想让它和区域5内的像素进行匹配。那么我们可以将像素0与区域3中的所有像素匹配结果都减去100(例如α 0 , 2 , α 0 , 3 , α 0 , 6 , α 0 , 7 等等),由于α 的值都很小,一般都是零点几的数,将其中一些数减去100后在通过SoftMax得到对应的权重都等于0了。所以对于像素0而言实际上还是只和区域5内的像素进行了MSA。那么对于其他像素也是同理,具体代码是怎么实现的,后面会在代码讲解中进行详解。注意,在计算完后还要把数据给挪回到原来的位置上(例如上述的A,B,C区域)。
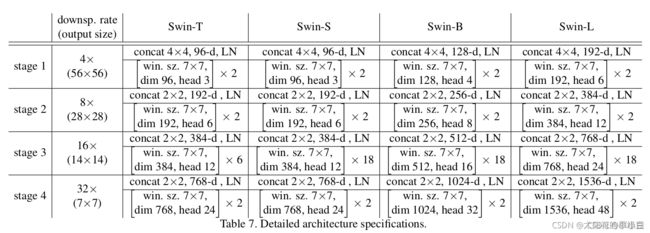
模型配置
下图是原论文中给出的关于不同Swin Transformer的配置,T(Tiny),S(Small),B(Base),L(Large),其中:
win. sz. 7x7表示使用的窗口(Windows)的大小
dim表示feature map的channel深度(或者说token的向量长度)
head表示多头注意力模块中head的个数
参考资料:https://blog.csdn.net/qq_37541097/article/details/121119988
公众号:NLP从入门到放弃