数据结构与算法--双向链表和双向循环链表
双向链表和双向循环链表
-
-
- 1. 双向链表
-
- 1.1 概念
- 1.2 双向链接的表结构
- 1.2 双向链接的创建和打印
- 1.3 双向链接的插入
- 1.4 双向链接的删除
-
- 1> 删除指定位置上的结点
- 2> 删除指定指定的元素
- 1.5 双向链接的元素查找和更新
-
- 1> 元素查找
- 2> 节点更新
- 2. 双向循环链表
-
- 2.1 概念
- 2.2 双向循环链表的创建和遍历
-
- 1> 创建
- 2.3 双向循环链表的插入
- 2.4 双向循环链表的删除
-
1. 双向链表
1.1 概念
双向链表顾名思义,就是链表由单向的链变成了双向链。 使用这种数据结构,可以不再拘束于单链表的单向创建于遍历等操作,大大减少了在使用中存在的问题。
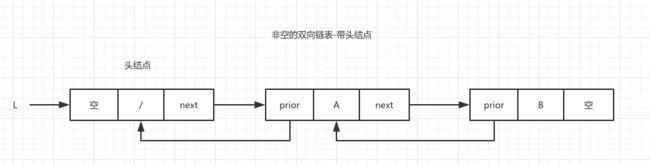
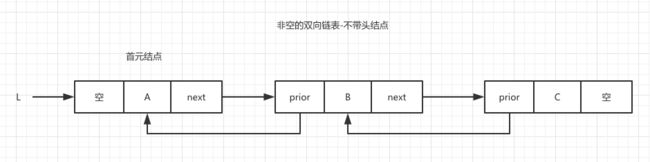
在单链表中,每个结点有一个数据域,还有一个指针域,数据域用来存储相关数据,而指针域则负责链表之间的“联系”。 而在双向链表中,每个需要有两个指针域,一个负责向后连接,一个负责向前连接。
一般在创建双线链表时,可以根据个人喜好是否添加一个头结点来指向首元节点。添加头节点时,在对双向链接做插入删除等一列操作时,不需要考虑首元节点的特殊情况。
1.2 双向链接的表结构
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define OK 1
#define MAXSIZE 20 /* 存储空间初始分配量 */
typedef int Status;/* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int ElemType;/* ElemType类型根据实际情况而定,这里假设为int */
//定义节点
typedef struct Node {
ElemType data; // s数据域
struct Node *prior; // 向前的指针
struct Node *next; // 向后的指针
}Node;
typedef struct Node * LinkList;
1.2 双向链接的创建和打印
在创建双向链表时,初始化一个头节点来标志链表的信息,代码如下:
// 创建
Status creatLinkList(LinkList *L) {
// *L 指向头结点
*L = (LinkList)malloc(sizeof(Node));
if (*L == NULL) return ERROR;
(*L)->prior = NULL;
(*L)->data = -1; // 设置一个特殊值
(*L)->next = NULL;
return OK;
}
//遍历
void show(LinkList L){
// 由头结点L 找到首元节点
LinkList temp = L->next;
if (temp == NULL) {
printf("打印的双向链表为空!\n");
return;
}
while (temp) {
printf("%d ",temp->data);
temp = temp->next;
}
printf("\n");
}
1.3 双向链接的插入
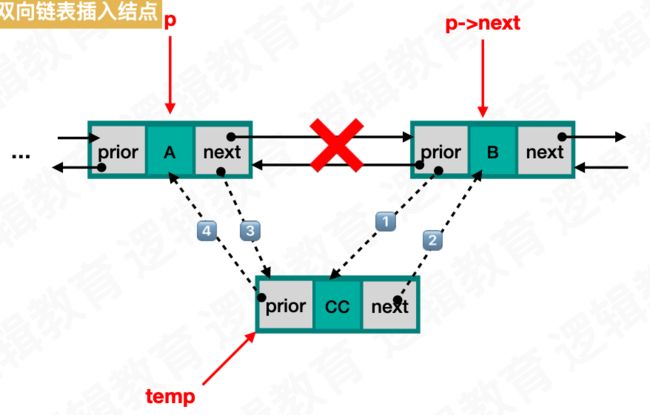
关键步骤:
1. 找到插入位置B节点的前一个节点p
2. 创建新节点 temp,将C节点的 next 指向 p 的 next
3. 将 p 的 next,即插入位置的 B 的 prior 指向 temp
4. 将 p->next 更新成新创建的temp
5. 将新创建的 temp 的前驱 prior 指向 p
Status ListInsert(LinkList *L, int i, ElemType data){
//1. 插入的位置不合法 为0或者为负数
if(i < 1) return ERROR;
//2. 新建节点
LinkList temp = (LinkList)malloc(sizeof(Node));
temp->data = data;
temp->prior = NULL;
temp->next = NULL;
//3.将p指向头结点!
LinkList p = *L;
//4. 找到插入位置i之前的结点
for(int j = 1; j < i && p;j++)
p = p->next;
//5. 如果插入的位置超过链表本身的长度
if(p == NULL){
printf("插入的位置超过链表本身的长度!\n");
return ERROR;
}
//6. 判断插入位置是否为链表尾部;
// 因为有头节点,所以对插入位置为1时,不用进行特殊处理
if (p->next == NULL) {
p->next = temp;
temp->prior = p;
}else
{
//1️⃣ 将p->next 结点的前驱prior = temp
p->next->prior = temp;
//2️⃣ 将temp->next 指向原来的p->next
temp->next = p->next;
//3️⃣ p->next 更新成新创建的temp
p->next = temp;
//4️⃣ 新创建的temp前驱 = p
temp->prior = p;
}
return OK;
}
1.4 双向链接的删除
1> 删除指定位置上的结点
关键步骤:
1.找到删除位置的前一个节点 p,
2.创建临时指针delTemp 指向要删除的结点,并将要删除的结点的data 赋值给*e,带回
3.将 p 的 next 指向被删除节点的 next
4.将被删除节点的 next 的 prior 指向 p
5.释放被删除的节点
代码:
Status ListDelete(LinkList *L, int i, ElemType *e){
int k = 1;
LinkList p = (*L);
//1.判断双向链表是否为空,如果为空则返回ERROR;
if (*L == NULL) return ERROR;
//2. 将指针p移动到删除元素位置前一个
while (k < i && p != NULL) {
p = p->next;
k++;
}
//3.如果k>i 或者 p == NULL 则返回ERROR
if (k>i || p == NULL) {
return ERROR;
}
//4.创建临时指针delTemp 指向要删除的结点,并将要删除的结点的data 赋值给*e,带回到main函数
LinkList delTemp = p->next;
*e = delTemp->data;
//5. p->next 等于要删除的结点的下一个结点
p->next = delTemp->next;
//6. 判断被删除结点的下一个结点不为空,则将将要删除的下一个结点的前驱指针赋值p;
if (delTemp->next != NULL) {
delTemp->next->prior = p;
}
//7.删除delTemp结点
free(delTemp);
return OK;
}
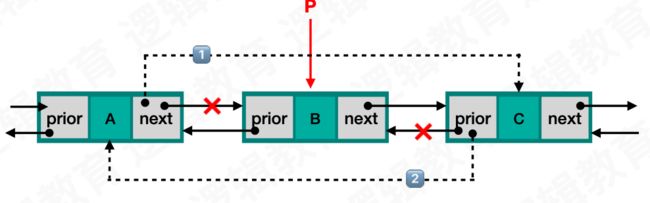
2> 删除指定指定的元素
关键步骤:
1.遍历双向循环链表
2.判断当前节点 p 的 data 是否等于指定的元素,相等,则p 为被删除的节点
3.将删除节点 p 的 prior 指向 p 的 next
4.被删除结点 p 的后继结点的前驱指针指向p 的 prior
5.释放被删除的节点
代码:
Status LinkListDeletVAL(LinkList *L, int data){
LinkList p = *L;
//1.遍历双向循环链表
while (p) {
//2.判断当前结点的数据域和data是否相等,若相等则删除该结点
if (p->data == data) {
//将删除节点 p 的 prior 指向 p 的 next
p->prior->next = p->next;
//被删除结点 p 的后继结点的前驱指针指向p 的 prior
if(p->next != NULL){
p->next->prior = p->prior;
}
//释放被删除结点p
free(p);
//退出循环
break;
}
//没有找到该结点,则继续移动指针p
p = p->next;
}
return OK;
}
1.5 双向链接的元素查找和更新
1> 元素查找
关键步骤:
1.创建变量i,记录位置,然后开始遍历双向循环链表
2.判断当前节点 p 的 data 是否等于指定的元素,
3.相等,记录位置,并返回
4.不相等,i++, p = p->next
5.遍历完成而没查找到,则返回-1,代表没有该元素
代码:
int selectElem(LinkList L,ElemType elem){
LinkList p = L->next;
// 创建变量i,记录位置
int i = 1;
while (p) {
// 判断当前节点 p 的 data 是否等于指定的元素,
if (p->data == elem) {
// 相等,记录位置,并返回
return i;
}
// 不相等,i++, p = p->next
i++;
p = p->next;
}
// 返回-1,代表没有该元素
return -1;
}
2> 节点更新
关键步骤:
1.定义变量 p,指向首元节点,
2.遍历找到要更新元素的节点
3.更新元素
代码:
Status replaceLinkList(LinkList *L,int index,ElemType newElem){
// 定义变量 p,指向首元节点,
LinkList p = (*L)->next;
// 遍历找到要更新元素的节点
for (int i = 1; i < index; i++) {
p = p->next;
}
// 更新元素
p->data = newElem;
return OK;
}
2. 双向循环链表
2.1 概念
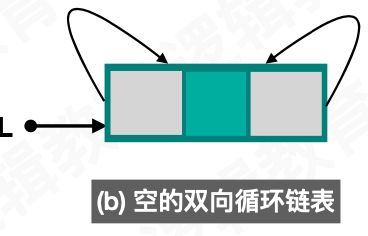
双向循环链表(默认有一个头结点作为辅助节点) 的节点和 双向链表 的节点是一样的。唯一的不同是,双向循环链表 的最后一个节点的后继指向头结点,头节点的前驱指向尾结点。
循环结束的条件是:
- 双向循环链表:节点的后继不等于头结点,即:
p-next != *L - 双向链表:尾节点的后继不等于
NULL,即:p-next != NULL
2.2 双向循环链表的创建和遍历
1> 创建
在创建双向循环链表时基本和双向链表的创建一样,初始化一个头节点来标志链表的信息,不同的是双向循环链表的next指向自己。
代码如下:
//创建
Status creatLinkList(LinkList *L){
*L = (LinkList)malloc(sizeof(Node));
if (*L == NULL) {
return ERROR;
}
(*L)->next = (*L);
(*L)->prior = (*L);
(*L)->data = -1; // 设置一个特殊值
return OK;
}
//遍历
Status show(LinkList L){
if (L == NULL) {
printf("打印的双向循环链表为空!\n\n");
return ERROR;
}
printf("双向循环链表内容: ");
LinkList p = L->next;
while (p != L) {
printf("%d ",p->data);
p = p->next;
}
printf("\n\n");
return OK;
}
2.3 双向循环链表的插入
主要步骤:
1.创建新节点 temp,对 temp 的数据域赋值,
2.找到插入位置的前一个节点 p
3.将新节点 temp 的 prior 指向 p
4.将新节点 temp 的 next,指向 p 的 next
5.将 p 的 next 指向新节点 temp
6.判断 temp 是不是最后一个节点。是,则头节点的 prior 指向 temp;
不是,则temp节点的下一个结点的前驱指向 temp 结点
代码:
Status ListInsert(LinkList *L, int index, ElemType e){
//1. 创建指针p,指向双向链表头
LinkList p = (*L);
int i = 1;
//2.双向循环链表为空,则返回error
if(*L == NULL) return ERROR;
//3.找到插入前一个位置上的结点p
while (i < index && p->next != *L) {
p = p->next;
i++;
}
//4.如果i>index 则返回error
if (i > index) return ERROR;
//5.创建新结点temp
LinkList temp = (LinkList)malloc(sizeof(Node));
//6.temp 结点为空,则返回error
if (temp == NULL) return ERROR;
//7.将生成的新结点temp数据域赋值e.
temp->data = e;
//8.将结点temp 的前驱结点为p;
temp->prior = p;
//9.temp的后继结点指向p->next;
temp->next = p->next;
//10.p的后继结点为新结点temp;
p->next = temp;
//11. temp 是不是最后一个节点。
if (*L != temp->next) {
//不是,则temp节点的下一个结点的前驱指向 temp 结点
temp->next->prior = temp;
}else{
// 是,则头节点的 prior 指向 temp;
(*L)->prior = temp;
}
return OK;
}
2.4 双向循环链表的删除
主要步骤:
1.判断是否删除到只剩头结点,是,直接置空
2.找到要删除的节点 p,并将 data 赋值给参数传回被删除的data
3.修改被删除结点的前驱结点的后继指针,即:将 p 的 prior 的 next 指向 p 的 next
4.修改被删除结点的后继结点的前驱指针,即:将 p 的 next 的 prior 指向 p 的 prior
5.释放删除的节点
Status LinkListDelete(LinkList *L,int index,ElemType *e){
int i = 1;
LinkList temp = (*L)->next;
if (*L == NULL) {
return ERROR;
}
// 如果删除到只剩下首元结点了,则直接将*L置空;
if(temp->next == *L){
free(*L);
(*L) = NULL;
return OK;
}
// 找到要删除的结点
while (i < index) {
temp = temp->next;
i++;
}
// 给e赋值要删除结点的数据域
*e = temp->data;
// 修改被删除结点的前驱结点的后继指针
temp->prior->next = temp->next;
// 修改被删除结点的后继结点的前驱指针
temp->next->prior = temp->prior;
// 删除结点temp
free(temp);
return OK;
}