基于逻辑回归的鸢尾花分类
二分类实现辨别是否是鸢尾花
尽管名为逻辑回归,但实际上是一个分类模型,尤其是在我们只有两个类时。逻辑回归的名称来源于将输入的任意实值x转换成值在0到1
采用sigmoid,划为[0,1]之间的数据 ,可以解释为概率
为了简单起见,我们将重点关注前两个特征:花萼长度——我们将其称为特征f1,花萼的宽度——我们将其称为特征f2。使用在线性回归中学习的技巧,我们可以把输入x表示成两个特征f1和f2的一个线性组合:
花瓣的长度和宽度、花萼的长度和宽度
x = w1f1 + w2f2
第一步加载数据集
import numpy as np
import matplotlib.pyplot as plt
import cv2
import sklearn
%matplotlib inline
from sklearn import datasets
from sklearn import linear_model
from sklearn import metrics
plt.style.use('ggplot')
iris = sklearn.datasets.load_iris()
iris 数据集分析:
directory
dir() 函数不带参数时,返回当前范围内的变量、方法和定义的类型列表;带参数时,返回参数的属性、方法列表。如果参数包含方法__dir__(),该方法将被调用。如果参数不包含__dir__(),该方法将最大限度地收集参数信息.
dir(iris) dir() # 获得当前模块的属性列表dir()
所有的数据点都包含在’data’中。有150个数据点,每个数据点有4个特征值:
dir(iris),iris.feature_names
(['DESCR',
'data',
'feature_names',
'filename',
'frame',
'target',
'target_names'],
['sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)'])
iris 数据集的directory:
[‘DESCR’, #description
‘data’, #完整数据
‘feature_names’, #特征的名字
‘filename’, #文件的所在地
‘frame’, #空值
‘target’, #label ,标签 ,(150,) [0,1,2] 三分类
‘target_names’] # array([‘setosa’, ‘versicolor’, ‘virginica’]
feature_names:
[‘sepal length (cm)’,
‘sepal width (cm)’,0
‘petal length (cm)’,
‘petal width (cm)’])
花瓣的长度和宽度、花萼的长度和宽度
np.unique(iris.target) #读取非重复元素 array([0, 1, 2])
array([0, 1, 2])
由于其内由三个数据为了让其 成为一个二分类的问题,
子轩需要将一些数据丢弃掉啊-_-!!
idx = iris.target !=2 #此时 数据中只留下了 bool类型
data = iris.data[idx].astype(np.float32) #传入bool类型,统计学习方法,筛选数据,还可以使用 x for x in Y if x<2 ?
target1 = list(filter(lambda x: x < 2,iris.target))
target = iris.target[idx].astype(np.float32)
target1 = np.array(target1)
np.unique(target1)
array([0, 1])
#生成器和迭代器
dict_list = {}
list0 = [x for x in range(5) if x]
list1 = [x for x in range(5,10)]
lambda高阶用法
fun1 = lambda x: x ** 2
iterable = filter(lambda x: x % 2, range(1, 10))
items1 = list(map(fun, iterable))
items2 = [x ** 2 for x in range(1, 10) if x % 2]
func = lambda x,y: x*10+y
func(1,2)
filter()
filter(fun,sequence)
is_odd = lambda x : x%2 == 1
newList = filter(is_odd,[1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
序列的每个元素作为参数传递给函数进行判断,
然后返回 True 或 False,最后将返回 True 的元素放到新列表中
map()
map(fun,sequence)
function – 函数
iterable – 一个或多个序列
第一个参数 function 以参数序列中的每一个元素调用 function 函数,
返回包含每次 function 函数返回值的新列表,返回迭代器
map(lambda x:x**2, [1,2,3,4,5])
map()和filter()都是对调用他们的数组进行遍历
参数上map函数与filter是一样的,他们的差别就是函数是对每个元素做一个数学上的代换,而非条件的判断
'''搞懂三个函数 map, lambda, filter'''
ls = [1,2,3,4,5]
map1 = list(map(lambda x:x**2,ls ))
filter1 = list(filter(lambda x: x<3,ls) )#迭代对象 ,可以进行迭代,也可以实例化
filter1
[1, 2]
map2 = np.array(ls)<3
map2
array([ True, True, False, False, False])
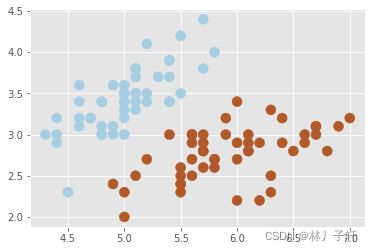
创建散点图,plt.scatter() ,检查数据,
x,y
c对应颜色指示值,也就是如果采用了渐变色的话,我们设置c=x就能使得点的颜色根据点的x值变化
cmap调整渐变色或者颜色列表的种类
s控制点大小
plt.scatter(data[:,0],data[:,1],c =target,cmap='Paired',s = 100)
数据集拆分
xTrain,xTest,yTrain,yTest = sklearn.model_selection.train_test_split(data,target,test_size=0.2,random_state=42) #返回ndarray 类型
xTrain.shape #(90, 4)
(80, 4)
'''sklearn 的分类器'''
lr = sklearn.linear_model.LinearRegression()
lr.fit(xTrain,yTrain)
yPre = lr.predict(xTest) #概率值
yPre = np.around(yPre,0).astype(int) # 概率值转变为预测的结果
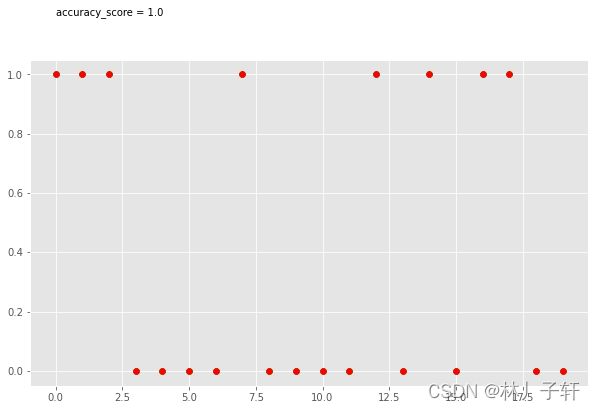
plt.figure(figsize=(10,6))
plt.scatter(range(yTest.size),yTest,c='g')
plt.text(0,1.2,f'accuracy_score = {metrics.accuracy_score(yTest,yPre)}')
plt.scatter(range(yTest.size),yPre,c = 'r')
'''cv2 的分类器'''
# 创建一个分类器的对象
logistRegression = cv2.ml.LogisticRegression_create()
# 指定一个训练方法
# cv2.ml.LogisticRegression_BATCH
# cv2.ml.LogisticRegression_MINI_BATH
logistRegression.setTrainMethod(cv2.ml.LOGISTIC_REGRESSION_MINI_BATCH)
logistRegression.setMiniBatchSize(1)
# 指定算法的迭代次数
logistRegression.setIterations(100)
# 训练模型
logistRegression.train(xTrain,cv2.ml.ROW_SAMPLE,yTrain)
#训练阶段的目标是找到一组最佳权重,将特征值转换为一个输出标签。单个数据点由它的4个特征值(f0、f1、f2和f3)给出
True
因为我们有4个特征,所以我们还应该有4个权重,使得x = w0f0 + w1f1 + w2f2 + w3f3,而且ŷ = σ(x)。但是,如前所述,该算法增加了一个额外的权重,它作为偏移量或偏置,使得x = w0f0 + w1f1 + w2f2 + w3f3 + w4
就意味着逻辑函数的输入是x = –0.0409f0 – 0.0191f1 – 0.163f2 + 0.287f3 + 0.119(偏置)
'''评估分类器的效果'''
ret,y_pred = logistRegression.predict(xTest) # 返回一个tuple,2维
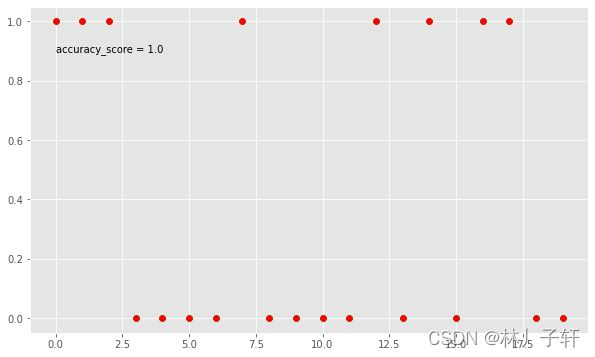
plt.figure(figsize=(10,6))
plt.scatter(range(yTest.size),yTest,c='g')
plt.text(0,0.9,f'accuracy_score = {metrics.accuracy_score(yTest,y_pred)}')
plt.scatter(range(yTest.size),y_pred,c = 'r')
plt.savefig('figures/iris_classification.png')