2022年蓝桥杯第二次校内选拔赛
河南农业大学校内赛
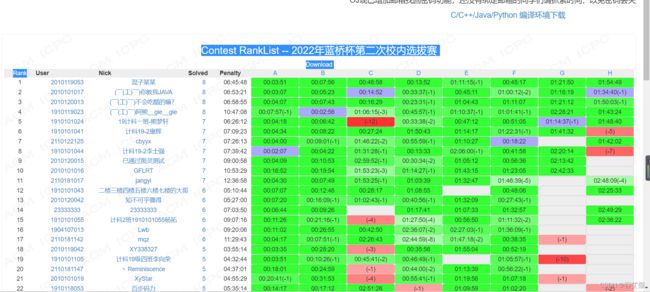
- 榜单
- 正文
-
- 问题 A: 单调数列
-
- 题目描述
- 题目思路及代码
- 问题 B: 最大连续1的个数
-
- 题目描述
- 题目思路及代码
- 问题 C: 祖玛游戏
-
- 题目描述
- 题目思路及代码
- 问题 D: 因数
-
- 题目描述
- 题目思路及代码
- E: 计算24
-
- 题目描述
- 题目思路及代码
- 问题 F: 子集和
-
- 题目描述
- 题目思路及代码
- G: 最大整除
-
- 题目描述
- 题目思路及代码
- H: 种树
-
- 题目描述
- 题目思路及代码
榜单
正文
问题 A: 单调数列
题目描述
题目描述
如果数组是单调递增或单调递减的,那么它是单调的。如果对于所有 i <= j,nums[i] <= nums[j],那么数组 nums 是单调递增的。 如果对于所有 i <= j,nums[i]> = nums[j],那么数组 nums 是单调递减的。当给定的数组 nums 是单调数组时输出"YES",否则输出"NO"。
输入
第一行输入一个正整数n表示数组大小(1<=n<=100000)
第二行输入n个[1,100000000]整数
输出
当给定的数组 nums 是单调数组时输出"YES",否则输出"NO"。
样例输入
4
4 3 2 1
样例输出
YES
题目思路及代码
签到题目
#include问题 B: 最大连续1的个数
题目描述
题目描述
给定一个正整数n,请你计算n在二进制表示下最大连续1的个数。例如:正整数55的二进制表示为110111,则答案为3。
输入
输入一个正整数n(1<=n<=1e9)
输出
输出n在二进制表示下最大连续1的个数
样例输入
55
样例输出
3
题目思路及代码
先转化为二进制,用一个简单队列获取结果
#include
if(a[i]==1){
r++;
}else{
l=i;
r=l;
}
ma=max(r-l,ma);
}
cout<<ma;
return 0;
}
问题 C: 祖玛游戏
题目描述
题目描述
给你一个只含有小写字母的字符串s,请你从左至右在 s 中选择第一个 k 个相邻且相等的字母,并删除它们,使被删去的字符串的左侧和右侧连在一起。你需要对 s 重复进行无限次这样的删除操作,直到无法继续为止。在执行完所有删除操作后,输出最终得到的字符串。
输入
整数k和字符串s,(2<=k<=5,1<=|s|<=1000000)
输出
输出执行完所有删除操作后最终得到的字符串。
样例输入
3
deeedbbcccbdaa
样例输出
aa
题目思路及代码
直接用暴力进行删除,知道不能在进行删除位置
#include
for(int i=x+1;i<(x+k);i++){
if(i>n)break;
if(str[i]==str[x]&&(i-x)<k){
//cout<
s++;
}
}
//cout<
if(s==k){
return 1;
}else{
return 0;
}
}
int main(){
cin>>k;
cin>>(str+1);
n=strlen(str+1);
ll cnt=0;
//ll k=0;
while(1){
//k++;
ll flag=0;
for(int i=1;i<=n;i++){
//cout<
//cout<
if(find1(i)){
//cout<
i=i+k-1;
flag=1;
//cout<
}else{
str1[++cnt]=str[i];
}
}
/*for(int i=1;i<=cnt;i++){
cout<
if(!flag){
break;
}
for(int i=1;i<=cnt;i++){
str[i]=str1[i];
}
n=cnt;
cnt=0;
}
for(int i=1;i<=cnt;i++){
cout<<str1[i];
}
return 0;
}
/*
2
deeedbbcccbdaa
*/
问题 D: 因数
题目描述
题目描述
给定正整数n,n只能被素因子2、3、5整除,请你求出正整数n能被2整除的因数个数。例如:n=6,6的因数为:1、2、3、6。答案为2。
输入
正整数n(1<=n<=1e16)
输出
求出正整数n能被2整除的因数个数
样例输入
6
样例输出
2
题目思路及代码
通过暴力获取结果,也可以通过唯一分解定理来求解,结果为a*(b+1)*(c+1)
#includeE: 计算24
题目描述
题目描述
游戏规则是:对4个 1∼10 之间的正整数,进行加、减、乘三种运算,要求运算结果等于二十四。乘法的优先级高于加、减,并且算式中不可以用括号,不可以改变4个数字出现的顺序。例如:若给出的 44个操作数是:10、2、4、8,则有2种可能的解答方案:10+2+4+8=24,10*2-4+8=24。现在给你4个1∼10 之间的正整数,请你计算解答方案数。
输入
4个 1∼10 之间的正整数
输出
输出方案总数
样例输入
10 2 4 8
样例输出
2
题目思路及代码
直接暴力枚举27种情况
#include问题 F: 子集和
题目描述
题目描述
给你一个元素个数不超过30的整数集合,请你计算该集合所有子集的元素之和。例如集合{1,4},则该集合的子集共四个{{空集}、{1}、{4}、{1、4}},则子集的元素之和为1+4+1+4=10。
输入
第一行一个正整数n(1<=n<=30)
第二行n个大小在[1,1000000]范围内的正整数
输出
输出给定集合所有子集的元素之和
样例输入
2
1 4
样例输出
10
题目思路及代码
直接用结论元素之和乘以2的n-1次方
#include=1;j--){
ll t=k&1;
k>>=1;
//k++;
if(t==1){
cnt+=a[j];
}
}
}*/
sum=sum*pow(2,n-1);
printf("%lld\n",sum);
return 0;
}
/*
*/
G: 最大整除
题目描述
题目描述
给你一个正整数k和一个整数数组 a,请你求出能被k整除的元素最大和。
输入
第一行两个正整数n和k,分别表示数组大小和题目中的k。(1<=n<=40000,2<=k<=20)
第二行n个[1,1000000]范围内的整数
输出
输出能被k整除的元素最大和。
样例输入
5 3
3 6 5 1 8
样例输出
18
提示
样例中选择3、6、1、8,3+6+1+8=18
题目思路及代码
动态规划,其实是背包变形,刚开始的代码为:
dp[0]=1;
for(ll i=1;i<=n;i++){
//dp[i]=1;
for(ll j=sum;j>=a[i];j--){
if(dp[j-a[i]]){
dp[j]=1;
}
}
}
但是经过计算后发现超时,因此需要进行取模来进行优化
#includeH: 种树
题目描述
题目描述
A市为了响应国家碳达峰碳中和目标要求,欲购买一批树苗来净化A市的空气。现有n个树苗厂家,每个厂家有一个初始树苗单价(单位元),每购买一颗树苗后,树苗单价都会上涨1元。现需要购买m颗树苗,问最少需要多少元。
输入
第一行两个正整数n和m(1<=n<=100000,1<=m<=1e10)
第二行n个[1,10]范围内的整数表示树苗厂家初始树苗单价。
输出
购买m颗树苗的最小花费
样例输入
3 6
1 2 3
样例输出
14
题目思路及代码
从小往大进行买树,不断计算是否买够,具体看代码
#include
ll k=(m-sum)/p.second;
cost += p.second*getmoney(p.first,p.first+k-1);
p.first += k;
k=(m-sum)%p.second;
cost += p.first*k;
sum += m-sum;
cout<<cost;
return 0;
}else{
cost += p.second*getmoney(p.first,q.first-1);
sum+= p.second*(q.first-p.first);
que.push({q.first,p.second+q.second});
}
//cout<
}
ll num = que.top().second;
ll jia = que.top().first;
//cout<
ll k=(m-sum)/num;
// cout<
cost += n*getmoney(jia,jia+k-1);
jia+=k;
k=(m-sum)%num;
cost += jia*k;
cout<<cost;
return 0;
}