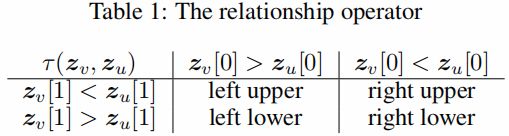Paper Information
Title:Geom-GCN: Geometric Graph Convolutional Networks
Authors:Hongbin Pei, Bingzhen Wei, K. Chang, Yu Lei, Bo Yang
Sources:2020, ICLR
Paper:Download
Code:Download
Abstract
Message-passing neural networks (MPNNs) 存在的问题:MPNNs 的 aggregator 限制了它们表示图结构数据的能力,即 丢失了节点与其邻居间的结构信息 和 无法捕获节点之间的长距离依赖关系。
本文提出的方案:A geometric aggregation scheme 。
本文的 Aggregation scheme 有三个 modules :node embedding、structural neighborhood、bi-level aggregation 。
直推式和归纳式:本文采取的是直推式。
本文模型:Geom-GCN
1 Intriduction
在每一层 MPNN 中,每个节点向其邻域内的节点发送其特征表示,即一条“消息”;然后通过聚合从邻域收到的所有“消息”来更新其特征表示。NPMM 采用的 aggregation function 具有平移不变性(permutation-invariant),比如 summation、maximum、mean 。
MPNNs 的 Aggregator 存在的问题一:Aggregator 丢失了节点与其邻居间的结构信息。比如 GCN 存在的问题:单纯聚集了一阶邻居的信息,并没有考虑节点标签的不一致性,不知道邻居节点到底贡献了什么。MPNNs 不能识别出异构图,这会造成的问题是 MPNNs 会将节点表示映射成一样,显然对异构图是不合适的。
对于问题一,用下述例子做解释:
同构图:同构图是指图中节点类型和关系类型(边的类型)都仅有一种。
异构图:与同构图相反,异构图指图中节点类型或关系类型多于一种。
问题二:Agrgregator 缺乏捕获远距离依赖的能力。
可能的解决方法:采用 multi-layered architecture 。当然这只是想想,原因是 1:distant node 无差别融合其近端 node 的信息(相关和不相关的信息)。2:图中的过平滑问题:即图中节点的表示最终将趋于一样。[ 理论上是同 label 的节点表示趋于一致,当然这也是因为其无法识别同构图和异构图,将不同类别的节点视为一类 ]
本文的思考:图上的聚合是否可以受益于 latent space,将节点映射为连续空间的一个向量(graph embedding),在隐空间查找邻居并进行聚合。
2 Geometric aggregation scheme
Geometric aggregation scheme 如 Fig. 1 所示:
Aggregation scheme 包括三个模块:node embedding (panel A1-A3)、structural neighborhood (panel B) 和 bi-level aggregation (panel C)。
2.1. Node embedding
将 Nodes 映射到 latent continous space 之中。记 Graph 为 $G=(V, E)$ ,其中节点 $v \in V$ 都有 fearure vector $x_{v}$ ,每个边 $e \in E$ 都连接两个节点,记 $f: v \rightarrow z_{v}$ 为一个映射函数,$f: v \rightarrow \boldsymbol{z}_{v}$ 将 Graph 中的节点$V$ 映射到 latent space,$\boldsymbol{z}_{v} \in \mathbb{R}^{d}$ 中 $\mathrm{d}$ 是 latent space 的维度。在映射过程中,Graph 的结构和属性都被保留下来,并表示为潜在空间中的几何形状。
2.2 Structural neighborhood
基于 Graph 和 latent space,我们构造了一个 Structural neighborhood, $N(v)=\left(\left\{N_{g}(v), N_{s}(v), \tau\right\}\right)$ ,用于下一层聚合,结构化的邻居包括节点集合 $\left\{N_{g}(v), N_{s}(v)\right\}$ 以及 Nodes 上的关系操作 $\tau$ 。
其中,图中的邻居集合定义为 $N_{g}(v)=\{u \mid u \in V,(u, v) \in E\}$ 代表与 $v$ 相连的邻居集合 [ 即邻接矩阵中的邻居 ],潜在空间中的邻居集合定义为 $N_{s}(v)=\left\{u \mid u \in V, d\left(\boldsymbol{z}_{u}, \boldsymbol{z}_{v}\right)<\rho\right\}$ 代表着与 $v$ 距离小于 $\rho$ 的邻居集合 [ 即根据相似性或者 distance 给出的邻居集合 ],从这可以看到 $N_{s}(v)$ 在一定程度上包括了长距离的 node 邻居,而且更具相似性。
关系操作算子(relational operator)是一个在潜在空间中定义的函数。其输入是 $v$ 和 $u$ 的有序位置对(ordered position pair) $\left(z_{v}, z_{u}\right) $ ,该算子用于表示 $v$ 和 $u$ 的几何关系。具体如下所示:
$\tau:\left(\boldsymbol{z}_{v}, \boldsymbol{z}_{u}\right) \rightarrow r \in R$
其中,$r$ 是离散值,$R$ 是几何关系的集合。对 $\tau$ 的一个要求是保证每个有序位置对只有一个几何关系,即生成的每个 $r$ 有且只有一个 [ 方便下文中 $(i,r)$ 进行索引 ]。
2.3 Bi-level aggregation
Bi-level aggregation 由两个聚合函数组成,并在一个神经网络层中进行操作。他可以在保证排列不变性的情况下,有效提取邻居节点的结构信息。
我们记 $\boldsymbol{h}_{v}^{l}$ 代表第 $l$ 层节点 $v$ 的 hidden features,$\boldsymbol{h}_{v}^{0}=\boldsymbol{x}_{v}$ 是 node features,$\boldsymbol{h}_{v}^{l}$ 并根据下述公式更新:
$\boldsymbol{e}_{(i, r)}^{v, l+1}=p\left(\left\{\boldsymbol{h}_{u}^{l} \mid u \in N_{i}(v), \tau\left(\boldsymbol{z}_{v}, \boldsymbol{z}_{u}\right)=r\right\}\right), \forall i \in\{g, s\}, \forall r \in R \quad \text { (Low-level aggregation) }$
$\boldsymbol{m}_{v}^{l+1}=\underset{i \in\{g, s\}, r \in R}{q}\left(\left(e_{(i, r)}^{v, l+1},(i, r)\right)\right)(\text{High-level aggregation})$
$\boldsymbol{h}_{v}^{l+1}=\sigma\left(W_{l} \cdot \boldsymbol{m}_{v}^{l+1}\right) (\text{Non-linear transform})$
对于 Low-level aggregation :将位于相同邻域且具有相同几何关系的节点的隐藏特征通过聚合函数 $p$ 聚合到一个虚拟节点(virtual node),我们定义虚拟节点的特征是 $e_{(i, r)}^{v, l+1}$。虚拟节点由 $(i,r)$ 进行索引,它对应于一个邻域 $i$ 和一个关系 $r$ 的组合。这里需要注意 $p$ 是具有平移不变性的函数,比如 $L_p$(通常 $p=1,2,\infty $)。Low-level aggregation 如 Fig. 1C 中的虚线箭头所示。
2.4 Comparisons to related work
为了克服第一个问题,本文利用潜在空间中的几何关系对邻域节点的结构信息进行明确的建模,然后利用 Bi-level aggregation 有效地提取信息。当前大多数研究在聚合特征时,尝试学习一些类似隐式结构的信息来区分不同的邻居。比如,使用注意力机制的有 GAT、 LGCL、GG-NN;使用 Covariance architecture 学习 Structure-aware representations 的 CCN 。
为了克服第二个问题,该方案以两种不同的方式对异质图中的长期依赖关系进行了建模。
-
- 一方面 [ 即 $N_s(v)$ ]:图中远距离的(但相似的)节点可以被映射到目标节点的一个基于潜在空间的邻域,然后它们有用的特征表示可以用于聚合。
- 另一方面 [ 即 $N_{g}(v)$ ],结 构信息使该方法能够区分基于图的邻域中的不同节点(如上所述)。信息节点可能与目标节点有一些特殊的几何关系(例如,特定的角度或距离),与无信息节点相比,目标节点的相关特征将被传递以更高的权重传递给目标节点(并保持传递给自己的邻居)。
3 Geom-GCN:An implementation of the scheme
Geometric aggregation scheme 在 GCN 中的具体实现,主要包括上述的三个模块: node embedding、structural neighborhood、aggregation function.
3.1 Node embedding
一个好的 Node embedding 可以更好的保存 其拓扑结构,这里采用三种 embedding method :Isomap(广泛使用的低维 Embedding method ,基于 distance )、Poincate、struc2vec(preserve hierarchies and local structures),对应于本文提出的方案 Geom-GCN-I、Geom-GCN-P、Geom-GCN-S
对于 $N_{s}(v)$ 中的 $\rho $ 我们将其区间范围设置为从 $0$ 直到 Average($N_{s}(v)$ ) = Average($N_{g}(v)$ ) ,这里的距离采用的是欧氏距离(Euclidean distance)。
本文,这里的几何算子 $\tau$ 定义为实现二维欧几里得空间和双曲空间中两个节点之间的相对位置的四种关系。Relationship set R= {left upper, right upper, left lower, right lower},$\tau\left(\boldsymbol{z}_{v}, \boldsymbol{z}_{u}\right)$ 定义如 Table 1 所示:
为实现 bi-level aggregation ,我们采用与GCN(Kipf&Welling,2017)相同的归一化隐藏特征之和,作为底层聚合中的聚合函数 $p$ 。
${\large \boldsymbol{e}_{(i, r)}^{v, l+1}=\sum\limits _{u \in N_{i}(v)} \delta\left(\tau\left(\boldsymbol{z}_{v}, \boldsymbol{z}_{u}\right), r\right)(\operatorname{deg}(v) \operatorname{deg}(u))^{\frac{1}{2}} \boldsymbol{h}_{u}^{l}, \forall i \in\{g, s\}, \forall r \in R} $
其中:
$\delta(\cdot, \cdot)$ 是一个只允许包含有关系的节点 $r$ 到 $v$ 的克罗内克增量函数
Aggregation function $q$ 是 concatenation 函数,具体如下:
${\large \boldsymbol{h}_{v}^{l+1}=\sigma\left(W_{l} \cdot \underset{i \in\{g, p\}}{||} \underset{r \in R}{||} \boldsymbol{e}_{(i, r)}^{v, l+1}\right)} $
其中:$\sigma $ 是非线性激活函数 ReLU 。
4 Experiments
本文定义 $\alpha$ 作为 Gromov hyperbolicity 用来测量图的双曲率。$\alpha$ 越小,空间越双曲,这表明图所具有的层次模式越强。
同样使用 $\beta$ 定义节点的同质性:
$\beta=\frac{1}{N} \sum\limits _{v \in V} \frac{\text { Number of } v \text { 's neighbors who have the same label as } v}{\text { Number of } v \text { 's neighbors }} .$
$\beta$ 值越大,说明就节点标签而言,节点对于给定图的同质性更强。
本文采用的数据库如 Table 2 所示:
实验结果如 Table 3 所示:
5 Conclusion and future work
我们解决了现有的信息传递神经网络在图上的两个主要缺点——鉴别结构的损失和长期依赖关系。作为我们的关键见解,我们通过图的嵌入将一个离散的图连接到一个连续的几何空间。也就是说,我们利用了卷积的原则:在一个有意义的空间上进行空间聚合——因此我们的方法从图中提取或“恢复”嵌入空间中丢失的信息(区分结构和长期依赖关系)。我们提出了一个通用的几何聚合方案,并用几个特定的Geom-GCN实现实例化了它,我们的实验验证了它的明显优势。作为未来的工作,我们将探索选择正确的嵌入方法的技术——不仅依赖于输入图,还依赖于目标应用程序。