【pytorch】踩坑记录

1. 叶子节点和非叶子节点
pytorch的tensor类中，有个叫is_leaf的属性，其为True则该变量为叶子节点，false则为非叶子节点。一般地：由用户自己创建的变量为叶子节点，网络层中的各层权重也为叶子节点。由叶子节点得到的中间变量为非叶子节点。

• 依赖于叶子节点的节点，requires_grad 属性默认为 True。
• 非叶子节点和叶子节点均不可执行 inplace 操作。inplace 指的是在不更改变量的内存地址的情况下，直接修改变量的值。
  以加法来说，inplace 操作有a += x，a.add_(x)，改变后的值和原来的值内存地址是同一个。非 inplace 操作有a = a + x，a.add(x)，改变后的值和原来的值内存地址不是同一个。
  参考

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
# y = (x + w) * (w + 1)
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)
# 在反向传播之前 inplace 改变了 w 的值，再执行 backward() 会报错
w.add_(1)
y.backward()

---

2. 反向传播后， 非叶子节点的梯度不会保存在内存中，如需保存非叶子节点的梯度，需调用retain_grad方法

import torch

a = torch.tensor([1.,2.,3.,4.,5.],requires_grad=True)
b = a[:2]
b.retain_grad()
c =2.* b.sum()
c.retain_grad()
c.backward()
print(b.grad)

3. 求导时，各级tensor需为float类型

---

4.梯度爆炸、loss在反向传播变为nan
原文链接：梯度爆炸、loss在反向传播变为nan

代码实现一：

def loss_function(x):
    mask = (x < 0.003).float()
    gamma_x = mask * 12.9 * x + (1-mask) * (x ** 0.5)
    loss = torch.mean((x - gamma_x) ** 2)
    return loss


x = torch.tensor([0, 0.0025, 0.5, 0.8, 1], requires_grad=True)
loss = loss_function(x)
print('loss:', loss)
loss.backward()
print(x.grad)

输出：

loss: tensor(0.0105, grad_fn=<MeanBackward0>)
tensor([    nan,  0.1416, -0.0243, -0.0167,  0.0000])

但此时仍然出现梯度爆炸，原因如下：

虽然gamma_x = mask * 12.9 * x + (1-mask) * (x ** 0.5)在结果上等同，

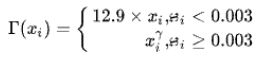
但在具体反向求导时，$x^{0.5}$在x=0时仍然参与了计算，并因此引发梯度爆照。
我们可以看以下代码进一步验证：

def loss_function(x):
  gamma_x = 0*x**0.5
  print("gamma_x\n",gamma_x)
  loss = torch.mean((x - gamma_x) ** 2)
  return loss

x = torch.tensor(([0, 0.0025, 0.5, 0.8, 1]), requires_grad=True)
loss = loss_function(x)
loss.backward()
print("x.grad\n",x.grad)

输出：

gamma_x
 tensor([0., 0., 0., 0., 0.], grad_fn=<MulBackward0>)
x.grad
 tensor([   nan, 0.0010, 0.2000, 0.3200, 0.4000])

虽然$gamm{a}_x=0\ast x^{0.5}$在数值上恒等于0，loss在数值上应为$loss=x^2$，但loss的表现形式为$loss=（x-gamma\_x{)}^2$,反向求导时，gamma_x仍参与计算，引发梯度爆炸。

改进代码二：

def loss_function(x):
    mask = x < 0.003
    gamma_x = torch.ones_like(x)
    gamma_x[mask] = 12.9 * x[mask]
    mask = x >= 0.003
    gamma_x[mask] = x[mask] ** 0.5
    loss = torch.mean((x - gamma_x) ** 2)
    return loss


x = torch.tensor(([0, 0.0025, 0.5, 0.8, 1]), requires_grad=True)
loss = loss_function(x)
print('loss:', loss)
loss.backward()
print(x.grad)

输出：

loss: tensor(0.0105, grad_fn=<MeanBackward0>)
tensor([ 0.0000,  0.1416, -0.0243, -0.0167,  0.0000])