【计算机视觉与深度学习】线性分类器(一)
目录
- 从线性分类器开始
- 线性分类器的定义
- 线性分类器的决策步骤
- 线性分类器的矩阵表示
- 线性分类器的 w i T \bm w_i^T wiT如何理解
- 线性分类器的决策边界
- 线性分类器的损失函数
-
- 损失函数的定义
- 多类支持向量机损失
从线性分类器开始
- 线性分类器形式简单,易于理解。
- 通过层级结构(神经网络)或高维映射(支持向量机)可以形成功能强大的非线性模型。
线性分类器的定义
线性分类器是一种线性映射,将输入的图像特征映射为类别分数。线性分类器定义如下: f i ( x , w i ) = w i T x + b i , i = 1 , 2 , . . . , c f_i(\bm x, \bm w_i)=\bm w_i^T \bm x+b_i,i=1,2,...,c fi(x,wi)=wiTx+bi,i=1,2,...,c其中 x \bm x x代表输入的 d d d维图像向量, c c c为类别个数, w i = [ w i 1 w i 2 . . . w i d ] T \bm w_i=\begin{gathered}\begin{bmatrix} w_{i1} & w_{i2} & ... & w_{id} \end{bmatrix}\end{gathered}^T wi=[wi1wi2...wid]T为第 i i i个类别的权值向量, b i b_i bi为偏置。如果 f i ( x ) > f j ( x ) f_i(\bm x)>f_j(\bm x) fi(x)>fj(x),则决策输入图像 x \bm x x属于第 i i i类。
线性分类器的决策步骤
- 将图像表示为向量。
假设我们有一张图片 [ 56 231 24 2 ] \begin{gathered}\begin{bmatrix} 56 & 231 \\ 24 & 2 \end{bmatrix}\end{gathered} [56242312]将其转换为向量的形式即为 x = [ 56 231 24 2 ] \bm x=\begin{gathered}\begin{bmatrix} 56 \\ 231 \\ 24 \\ 2 \end{bmatrix}\end{gathered} x=⎣⎢⎢⎡56231242⎦⎥⎥⎤ - 计算当前图片每个类别的分数。
假设我们当前需要完成的是一个三分类任务(将图片划分为汽车类、猫类、鸟类的其中一种),线性分类器为 f i ( x , w i ) = w i T x + b i , i = 1 , 2 , 3 f_i(\bm x, \bm w_i)=\bm w_i^T \bm x+b_i,i=1,2,3 fi(x,wi)=wiTx+bi,i=1,2,3其中权值矩阵 w i T = [ 0.2 − 0.5 0.1 2.0 1.5 1.3 2.1 0.0 0 0.25 0.25 − 0.3 ] \bm w_i^T=\begin{gathered}\begin{bmatrix} 0.2 & -0.5 & 0.1 & 2.0 \\ 1.5 & 1.3 & 2.1 & 0.0 \\ 0 & 0.25 & 0.25 & -0.3 \end{bmatrix}\end{gathered} wiT=⎣⎡0.21.50−0.51.30.250.12.10.252.00.0−0.3⎦⎤偏置 b i = [ 1.1 3.2 − 1.2 ] b_i=\begin{gathered}\begin{bmatrix} 1.1 \\ 3.2 \\ -1.2 \end{bmatrix}\end{gathered} bi=⎣⎡1.13.2−1.2⎦⎤也就是说,对于汽车类,有 w 1 T = [ 0.2 − 0.5 0.1 2.0 ] \bm w_1^T=\begin{gathered}\begin{bmatrix} 0.2 & -0.5 & 0.1 & 2.0 \end{bmatrix}\end{gathered} w1T=[0.2−0.50.12.0]对于猫类,有 w 2 T = [ 1.5 1.3 2.1 0.0 ] \bm w_2^T=\begin{gathered}\begin{bmatrix} 1.5 & 1.3 & 2.1 & 0.0 \end{bmatrix}\end{gathered} w2T=[1.51.32.10.0]对于鸟类,有 w 3 T = [ 0 0.25 0.25 − 0.3 ] \bm w_3^T=\begin{gathered}\begin{bmatrix} 0 & 0.25 & 0.25 & -0.3 \end{bmatrix}\end{gathered} w3T=[00.250.25−0.3]我们很容易就能求得步骤1中的图片向量 x \bm x x在3个类别的得分 f i ( x ) ( i = 1 , 2 , 3 ) . f_i(\bm x)(i=1,2,3). fi(x)(i=1,2,3).下面给出计算过程: f 1 ( x ) = w 1 T x + b 1 = − 96.8 f_1(\bm x)=\bm w_1^T \bm x+b_1=-96.8 f1(x)=w1Tx+b1=−96.8 f 2 ( x ) = w 2 T x + b 2 = 437.9 f_2(\bm x)=\bm w_2^T \bm x+b_2=437.9 f2(x)=w2Tx+b2=437.9 f 3 ( x ) = w 3 T x + b 3 = 61.95 f_3(\bm x)=\bm w_3^T \bm x+b_3=61.95 f3(x)=w3Tx+b3=61.95 - 按类别分数判定当前图像的类别。
根据上面的计算结果,我们判定图像应属于第2类,即猫类。
线性分类器的矩阵表示
线性分类器的矩阵表示为 f ( x , W ) = W x + b \bm f(\bm x,\bm W)=\bm W \bm x+ \bm b f(x,W)=Wx+b其中, x \bm x x代表输入图像,其维度为 d d d; f \bm f f为分数向量,其维度等于类别个数 c c c; W = [ w 1 w 2 . . . w c ] T \bm W=\begin{gathered}\begin{bmatrix} \bm w_1 & \bm w_2 & ... & \bm w_c \end{bmatrix}\end{gathered}^T W=[w1w2...wc]T为权值矩阵, w i = [ w i 1 w i 2 . . . w i d ] T \bm w_i=\begin{gathered}\begin{bmatrix} w_{i1} & w_{i2} & ... & w_{id} \end{bmatrix}\end{gathered}^T wi=[wi1wi2...wid]T为第 i i i个类别的权值向量; b = [ b 1 b 2 . . . b c ] T \bm b=\begin{gathered}\begin{bmatrix} b_1 & b_2 & ... & b_c \end{bmatrix}\end{gathered}^T b=[b1b2...bc]T为偏置向量, b i b_i bi为第 i i i个类别的偏置。
线性分类器的 w i T \bm w_i^T wiT如何理解
下面以CIFAR-10数据集(每张图片样本的大小为32×32×3)为例,将线性分类器的权值向量 w i \bm w_i wi转化为32×32×3的矩阵,并将数值归化到 [ 0 , 255 ] [0,255] [0,255]区间,以图片的形式表示:

可见,上面的每一个模板都记录了每一个类别的统计信息。待决策图片与模板图片越相似,根据线性分类器的定义计算出的类别分数 f f f就越大。
总结一下,权值可以看做是一种模板,输入图像与评估模板的匹配程度越高,分类器输出的分数就越高。
线性分类器的决策边界
从几何学角度来说,对于具有二维特征的图片分类问题,类别分数等于0的线,即 w i T x + b i = 0 , i = 1 , 2 , . . . , c \bm w_i^T \bm x+b_i=0,i=1,2,...,c wiTx+bi=0,i=1,2,...,c就是决策面。推广到更高维特征的图片依旧适用。分类器实质上学习的就是决策边界。权值 w \bm w w控制着决策边界的方向,偏置 b b b控制着决策边界的偏移。在上图中,箭头方向代表分类器的正方向,沿着分类器的正方向距离决策边界越远,类别分数就越高。
线性分类器的损失函数
损失函数的定义
损失函数搭建了模型性能与模型参数之间的桥梁,指导模型参数优化。损失函数用于度量给定分类器的预测值与真实值的不一致程度,其输出通常是一个非负实值,该值可以作为反馈信号来对分类器参数进行调整,以降低当前示例对应的损失值,提升分类器的分类效果。
损失函数的一般定义为 L = 1 N ∑ i L i ( f ( x i , W ) , y i ) L=\frac{1}{N}\sum_iL_i(f(\bm x_i,\bm W),y_i) L=N1i∑Li(f(xi,W),yi)其中 x i \bm x_i xi表示数据集中第 i i i个样本, f ( x i , W ) f(\bm x_i,\bm W) f(xi,W)表示分类器对 x i \bm x_i xi的类别预测, y i y_i yi为样本 i i i的真实类别标签, L i L_i Li为第 i i i个样本的损失值, L L L为数据集的损失值,是数据集中所有样本损失的平均值。
多类支持向量机损失
记线性分类器为 s i j = f j ( x i , w j , b j ) = w j T x i + b j s_{ij}=f_j(\bm x_i,\bm w_j,b_j)=\bm w_j^T \bm x_i+b_j sij=fj(xi,wj,bj)=wjTxi+bj其中 j j j表示类别标签, j = 1 , 2 , . . . , c j=1,2,...,c j=1,2,...,c, w j , b j \bm w_j,b_j wj,bj表示第 j j j个类别分类器的参数, x i \bm x_i xi表示数据集中的第 i i i个样本, s i j s_{ij} sij表示第 i i i个样本第 j j j类别的预测分数。则第 i i i个样本的多类支持向量机损失定义为 L i = ∑ j ≠ y i max ( 0 , s i j − s y i + 1 ) L_i=\sum_{j\neq y_i}\max(0,s_{ij}-s_{y_i}+1) Li=j=yi∑max(0,sij−syi+1)其中 s y i s_{y_i} syi表示第 i i i个样本真实类别的预测分数。损失函数中在 s i j − s y i s_{ij}-s_{y_i} sij−syi后面加 1 1 1是加了一个边界,这样可以使损失值的计算更稳定。当正确类别的得分比不正确类别的得分高出1分及以上时,就没有损失,否则就会产生损失。

max ( 0 , ⋅ ) \max(0,·) max(0,⋅)损失常被称为折页损失 (hinge loss)。
下面给出一组多类支持向量机损失的计算示例。
假设有三个类别的训练样本各一张,线性分类器为 f ( x , W ) = W x + b \bm f(\bm x,\bm W)=\bm W \bm x+\bm b f(x,W)=Wx+b,其中 W , b \bm W,\bm b W,b已知,分类器对三个样本的打分如下:
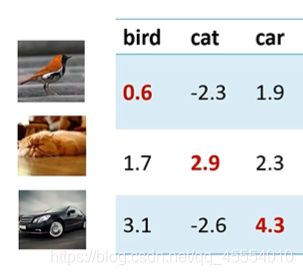
当前分类器对于样本1的损失为 L 1 = max ( 0 , − 2.3 − 0.6 + 1 ) + max ( 0 , 1.9 − 0.6 + 1 ) = 2.3 L_1=\max(0,-2.3-0.6+1)+\max(0,1.9-0.6+1)=2.3 L1=max(0,−2.3−0.6+1)+max(0,1.9−0.6+1)=2.3对于样本2的损失为 L 2 = max ( 0 , 1.7 − 2.9 + 1 ) + max ( 0 , 2.3 − 2.9 + 1 ) = 0.4 L_2=\max(0,1.7-2.9+1)+\max(0,2.3-2.9+1)=0.4 L2=max(0,1.7−2.9+1)+max(0,2.3−2.9+1)=0.4对于样本3的损失为 L 3 = max ( 0 , 3.1 − 4.3 + 1 ) + max ( 0 , − 2.6 − 4.3 + 1 ) = 0 L_3=\max(0,3.1-4.3+1)+\max(0,-2.6-4.3+1)=0 L3=max(0,3.1−4.3+1)+max(0,−2.6−4.3+1)=0则当前分类器对于整个数据集图像的损失为 L = 1 N ∑ i = 1 N L i = 2.3 + 0.4 + 0 3 = 0.9 L=\frac{1}{N}\sum_{i=1}^NL_i=\frac{2.3+0.4+0}{3}=0.9 L=N1i=1∑NLi=32.3+0.4+0=0.9
