强化学习学习笔记——马尔可夫决策过程（一）

前言

虽然不是第一次学强化学习的内容，但这确实是我第一次在网上开始写学习笔记。
写学习笔记的原因有两个：

1. 首先是因为，自己学了好久都学不明白，现在开始下决心把这套东西学透。学习笔记有助于我整理学习的思路，相当于再自己复习一遍，看能否用自己的话把所学的东西说明白。也借用各位的评价来审视自己的理解是否有误。
2. 希望用这种方式丰富一下自己的生活，经营一个我自己的博客。借此，希望逼迫自己坚持下来。毕竟我还是缺乏一点点毅力。

这里，我需要说明的是，我学强化学习的资料比较杂，手头目前有一本PDF版的《深入浅出强化学习》（郭宪 方勇纯编著）（以后称它为“教程”），但之前看的时候就发现有挺多笔误，字体也是挺奇怪的，比如“门”字用的是“冂”上加一短竖，读起来挺费劲。除了主要参考这一本书以外，看不懂的时候就网上找资料，弄明白为止。

在用到网上参考资料的时候，我尽量给出出处吧。毕竟我的理解和其他人的理解可能不一样。看原文能够最大可能的避免“理解”上的“偏移”。

以上是一堆废话，下面正式开始。

强化学习

机器学习分为：有/无监督学习，强化学习

• 有/无监督学习：面向的是静态数据，没有与动态环境的交互。我的理解是，它就是用来识别/分类的。
• 强化学习：面向的是动态数据，有与环境的交互以及实时的数据更新。用来交互/决策的。

此外，深度学习和强化学习可以结合，形成成深度强化学习。

• 深度学习：解决了感知问题
• 强化学习：解决了决策问题

从马尔科夫开始

为什么强化学习都从马尔科夫开始呢？
因为强化学习解决的是“序贯决策”问题，与之对应的是单阶段决策。

• 序贯决策：按时间顺序排列起来，以得到按顺序的（动态的）各种决策结果。
• 但阶段决策：决策者只需要做出一次决策即可。

根据教程，“一般的序贯决策问题可以利用马尔科夫决策过程的框架来表述”（说明：这里我不懂为什么，但接受就好，有空再细研究），因此我们需要从马尔科夫开始学起。

渐进地，要学马尔科夫决策过程，我们需要从以下几个点，层层递进，逐渐学起

• 马尔科夫性
• 马尔科夫过程
• 马尔科夫奖励过程
• 马尔科夫决策过程

马尔科夫性

什么是马尔科夫性？

假设有一只马尔科夫蛙在2B荷叶上，这只蛙忘性大，它永远记不住自己是从哪儿跳到目前这个荷叶上的。那么，现在它累了，想跳到别的荷叶上去。它将跳到哪个荷叶上？有可能是3A，也可能是1C，还可能是2B（忘性太大），这决定于马尔科夫蛙自己的决策策略。好了，故事结束了，下课。

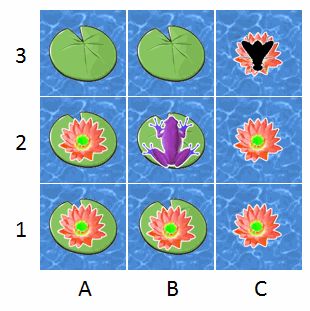
上面故事中，马尔科夫蛙就是决策者（或者叫”Agent“，教程中叫”智能体“），它目前所在的2B荷叶就是当前所处的状态（State），那么它跳向的下一个荷叶（状态）只与它当前所处的荷叶有关，与之前的它从哪儿跳来的无关。这就是马尔科夫性。

• 定义：所谓马尔科夫性是指，系统下一个状态$s_{t+1}$只于当前状态$s_t$有关，而与以前的状态无关。

故事继续，这只蛙不断跳啊跳，我们记录下它每次跳的荷叶编号，形成一个状态序列，这就是马尔科夫链。那么，这只青蛙的马尔科夫链可能是：
2B-3A-1C-2A-1A-3A…
2B-2C-1A-1C-3A-3C…
2B-2B-2B-2B-2B-2B…
…

上面可能有无穷多种马尔科夫链，但是链上每一个状态都是符合马尔科夫性的。上述蛙选择跳跃的过程就是马尔科夫过程。

马尔科夫过程

定义：马尔科夫过程是一个二元组$(S,P)$，并且满足以下条件：

• $S$是有限状态的集合：$S=\{s_1,s_2,\cdots ,s_n\}$
• $P$是状态转移的概率，概率矩阵可以表示为：$$P=\left[\begin{array}{ccc}{p}_{s_1->s_1}& \cdots & p_{s_1->s_n}\\ \dots & & \dots \\ p_{s_n->s_1}& \cdots & p_{s_n->s_n}\end{array}\right]$$

其中$p_{s_i->s_j}$表示从状态$s_i$跳转到状态$s_j$的概率。很明显，$P$矩阵的每一行之和、每一列之和都为1。

还以马尔科夫蛙为例，状态集合为$S=\{1A,1B,1C,2A,2B,2C,3A,3B,3C\}$这些荷叶，表示它当前所在的位置，状态转移矩阵表示马尔科夫蛙在当前荷叶有多大可能跳向某一个荷叶。

未完待续…