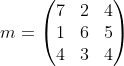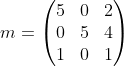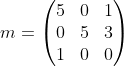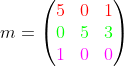匈牙利算法--任务分配
参考博客
参考博客2
参考博客3
一、背景介绍
例如有3个任务ABC,要分配给甲乙丙三人分别去完成,每个人完成3个任务所耗费精力不同(因为每个人特长不同),此处也叫完成任务耗费的代价,合理分配任务,可以达到总效率最高的目标。
例如:
甲乙丙完成ABC三个任务,花费的精力分别为:
| A | B | C | |
| 甲 | 7 | 2 | 4 |
| 乙 | 1 | 6 | 5 |
| 丙 | 4 | 3 | 4 |
此时若想达到耗费总精力最小,可以用穷举法一个个试,一共有6种组合,分别是:
1:甲A,乙B,丙C 7+6+4=17
2:甲A,乙C,丙B 7+5+3=15
3:甲B,乙A,丙C 2+1+4=7
4:甲B,乙C,丙A 2+5+4=11
5:甲C,乙A,丙B 4+1+3=8
6:甲C,乙B,丙A 4+6+4=14
所以方案3最符合需求
对于任务数和执行者数目较少时,用穷举法尚可,但是若任务数很大时,穷举数目也将以n!的形势增加,匈牙利算法的提出就是为了优化这个问题。
二、匈牙利算法
将上面所提的任务和执行人耗费精力的值,用矩阵来记录,则为一个3X3的矩阵
矩阵每行减去该行最小元素
接着矩阵每列减去该列最小元素
用最少的横线或竖线覆盖所有含0的行或列,若线数目=n则算法结束
算法步骤:
1.每行元素减去行最小
2.每列元素减去列最小
3.用虽少的横竖线覆盖0元素,若横竖线数目=n,则结束,否则执行4
4.横竖线未覆盖区域取最小值m,未覆盖的元素所在行元素-m,已覆盖的列元素+m
5.重复4直到结束
三、代码实现
import itertools
import numpy as np
from numpy import random
from scipy.optimize import linear_sum_assignment
# 任务分配类
class TaskAssignment:
# 类初始化,需要输入参数有任务矩阵以及分配方式,其中分配方式有两种,全排列方法all_permutation或匈牙利方法Hungary。
def __init__(self, task_matrix, mode):
self.task_matrix = task_matrix
self.mode = mode
if mode == 'all_permutation':
self.min_cost, self.best_solution = self.all_permutation(task_matrix)
if mode == 'Hungary':
self.min_cost, self.best_solution = self.Hungary(task_matrix)
# 全排列方法
def all_permutation(self, task_matrix):
number_of_choice = len(task_matrix)
solutions = []
values = []
for each_solution in itertools.permutations(range(number_of_choice)): #对0 1 2进行排列组合,每个each_solution代表一个组合
each_solution = list(each_solution)
solution = []
value = 0
for i in range(len(task_matrix)):
value += task_matrix[i][each_solution[i]] #按各种组合将最终代价加出来
#print(task_matrix[i][each_solution[i]]) #00+11+22 00+12+21 01+10+22 01+12+20
solution.append(task_matrix[i][each_solution[i]])
values.append(value)
solutions.append(solution) #每个组合的n个值
min_cost = np.min(values)
best_solution = solutions[values.index(min_cost)]
return min_cost, best_solution
# 匈牙利方法
def Hungary(self, task_matrix):
b = task_matrix.copy()
# 行和列减0
for i in range(len(b)): #行数
row_min = np.min(b[i]) #第i行最小值
for j in range(len(b[i])):
b[i][j] -= row_min #行每个元素减去行最小值
for i in range(len(b[0])):
col_min = np.min(b[:, i])#每列从0:2
for j in range(len(b[:, i])):
b[j][i] -= col_min #列每个元素减去列最小
line_count = 0
# 线数目小于矩阵长度时,进行循环
while (line_count < len(b)):
print('b=\n',b)
line_count = 0
row_zero_count = []
col_zero_count = []
for i in range(len(b)):
#print(b[i] == 0)
row_zero_count.append(np.sum(b[i] == 0)) #b[i] == 0 true false true 判断矩阵每行有几个0,然后把个数记录在row_zero_count里面
print(row_zero_count)
for i in range(len(b[0])):
col_zero_count.append((np.sum(b[:, i] == 0))) #判断矩阵每列有几个0,然后把个数记录在col_zero_count里面
#print(col_zero_count)
# 划线的顺序(分行或列)
line_order = []
row_or_col = []
for i in range(len(b[0]), 0, -1): #此循环为了将行列的0用横竖线全覆盖,横线的row_or_col记为0,竖线的row_or_col记为1
#print(i,'pppp ')
while (i in row_zero_count):
line_order.append(row_zero_count.index(i))
#print(i,' ',line_order,' ',row_zero_count.index(i)) #row_zero_count.index(i)含义是row_zero_count中i的序号
row_or_col.append(0)
#用来跳出while
row_zero_count[row_zero_count.index(i)] = 0
#print(row_zero_count)
while (i in col_zero_count):
line_order.append(col_zero_count.index(i))
row_or_col.append(1)
col_zero_count[col_zero_count.index(i)] = 0
# 画线覆盖0,并得到行减最小值,列加最小值后的矩阵
delete_count_of_row = []
delete_count_of_rol = []
row_and_col = [i for i in range(len(b))] # i=for i in range(len(b))的每个值
#print(len(line_order))
#print('b=\n',b,'\n')
for i in range(len(line_order)):
if row_or_col[i] == 0: #如果是横线
delete_count_of_row.append(line_order[i])
else: #竖线
delete_count_of_rol.append(line_order[i])
c = np.delete(b, delete_count_of_row, axis=0) #axis=0 按行删除,删除第delete_count_of_row行
c = np.delete(c, delete_count_of_rol, axis=1) #按列删除
print('c=\n',c,'\n')
line_count = len(delete_count_of_row) + len(delete_count_of_rol)
print('i=',i,' ',delete_count_of_row,' ',delete_count_of_rol)
# 线数目等于矩阵长度时,跳出
if line_count == len(b):
break
# 判断是否画线覆盖所有0,若覆盖,进行加减操作
if 0 not in c: #此处对中间矩阵b不断更新,直到最小划线数=n
print('-----------------\n')
row_sub = list(set(row_and_col) - set(delete_count_of_row))
min_value = np.min(c)
print(row_sub,' ',min_value)
for i in row_sub:
b[i] = b[i] - min_value #未被覆盖的行均减去最小值
for i in delete_count_of_rol:
b[:, i] = b[:, i] + min_value #被覆盖的列均加最大值
break
#其实此处之上的代码完全可以不用,直接使用linear_sum_assignment(task_matrix)就是最终解,上方代码可以作为匈牙利算法执行逻辑的展现
row_ind, col_ind = linear_sum_assignment(b) #线性和分配问题 匈牙利算法函数包,直接输入task_matrix即可返回每行对应最小的列, 0 1 2,0 2 1
print(row_ind,' ',col_ind)
min_cost = task_matrix[row_ind, col_ind].sum() #012 120 01 12 20
best_solution = list(task_matrix[row_ind, col_ind])
return min_cost, best_solution
# 这个叫随机种子数,它一旦固定,则后续结果都是可以复现的。
rd = random.RandomState(1000)
task_matrix = rd.randint(0, 100, size=(4, 4))
# 用全排列方法实现任务分配
ass_by_per = TaskAssignment(task_matrix, 'all_permutation')
# 用匈牙利方法实现任务分配
ass_by_Hun = TaskAssignment(task_matrix, 'Hungary')
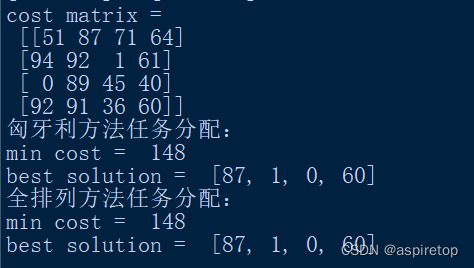
print('cost matrix = ', '\n', task_matrix)
print('匈牙利方法任务分配:')
print('min cost = ', ass_by_Hun.min_cost)
print('best solution = ', ass_by_Hun.best_solution)
print('全排列方法任务分配:')
print('min cost = ', ass_by_per.min_cost)
print('best solution = ', ass_by_per.best_solution)
print('\n',linear_sum_assignment(task_matrix))
简单版:
import numpy as np
from numpy import random
from scipy.optimize import linear_sum_assignment
# 这个叫随机种子数,它一旦固定,则后续结果都是可以复现的。
rd = random.RandomState(1000)
task_matrix = rd.randint(0, 100, size=(4, 4))
print('task_matrix =\n',task_matrix)
row_ind, col_ind = linear_sum_assignment(task_matrix) #线性和分配问题 匈牙利算法函数包,直接输入task_matrix即可返回每行对应最小的列
min_cost = task_matrix[row_ind, col_ind].sum()
best_solution = list(task_matrix[row_ind, col_ind])
print('min_cost =',min_cost)
print('best_solution =',best_solution)