Toward Geometric Deep SLAM--Daniel DeTone && Tomasz Malisiewicz
D Detone, Malisiewicz T , Rabinovich A . Toward Geometric Deep SLAM[J]. 2017.
本文使用深度学习来估计帧间图像的单应性矩阵,主要分成两步:第一步通过一个卷积神经网络找到输入图像中的角点;第二步的输入是两个角点图(概率),即两幅帧间图像分别通过第一个卷积神经网络得到的点图(概率),输出为9个数字,即 H 3 ∗ 3 H_{3*3} H3∗3单应性矩阵
- 1、总体结构
- 2、MagicPoint
-
- 2.1、MagicPoint结构
- 2.2、MagicPoint网络的训练
- 2.3、MagicPoitn网络的Loss
- 3、MagicWarp
-
- 3.1、结构
- 3.2、训练
- 3.3、损失函数
- 4、效果
-
- 4.1、MagicPoint效果
-
- 4.1.1、平均精度和定位误差
- 4.1.2、不同噪声程度下的角点检测效果
- 4.1.3、不同噪声类型下的角点检测效果
- 4.1.4、不同静态场景下角点检测效果
- 4.2、MagicWarp效果
-
- 4.2.1、MagicWarp的匹配能力
- 4.2.2、展示匹配效果
- 4.2.3、四种变换在不同强度下,MagicWarp的效果
- 4.3、附录展示MagicPoint的效果
1、总体结构
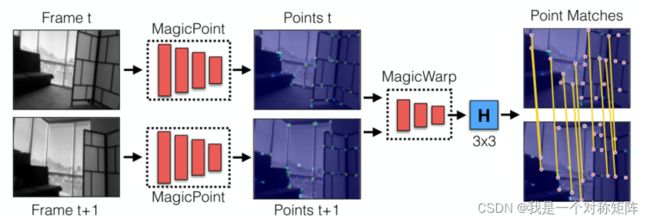
该论文设计了两个卷积神经网络:MagicPoint和MagicWarp:
- MagicPoint负责找寻图像中的角点,即输入图像,输出角点概率图。
- MagicWarp负责计算单应性矩阵,即同时输入两个图的角点概率图,输出两幅图之间的单应性矩阵。
注意MagicWarp的输出就是 H 3 ∗ 3 的 9 个 数 字 H_{3*3}的9个数字 H3∗3的9个数字,最后的matches是计算loss时的步骤了,后面细讲。
2、MagicPoint
2.1、MagicPoint结构

输入为灰度图,通过VGG-like的encoding得到65通道的特征图,通过softmax转换为概率,最终得到152065的tensor(因为输入是120160),它代表着输入图中局部88像素区域每个像素为角点的概率。通道数为8*8+1,为什么+1,这个代表垃圾通道,表示在该区域没有检测到角点。
为了将结果show出来,上图中最后舍弃了垃圾通道,将122064的tensor重新reshape为一个heatmap,就可以将预测出来的角点位置可视化出来。
(个人理解为,对于tensor左上角的一个点,有65个通道,即1*1*64+1*1*1,1x1表示原图中8*8的像素像素区域,该像素区域有64个像素点,这64个像素点中哪些是角点?刚好64个通道值就表示64个像素为角点的概率。第65个通道表示这64个像素点是否都没有角点)
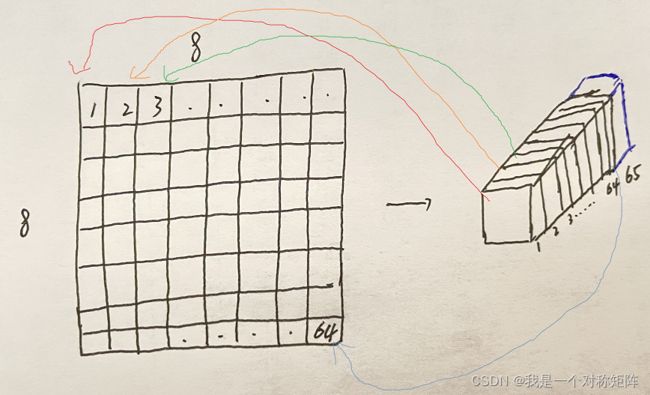
(但是感觉有点牵强,竟然能解释通道的含义??但是论文中暂时没看到详细的解释)
2.2、MagicPoint网络的训练
因为没有准备好的较大的数据集,所以他们自己曲线救国设计了新的方法。使用Opencv生成一系列的图,于是就有了训练图像和角点的位置:

同时还增加了噪声增加鲁棒性:

2.3、MagicPoitn网络的Loss
使用:cross entropy loss
3、MagicWarp
3.1、结构
结构图如下,至此我们可以看到整个流程,通过MagicPoint检测角点位置,将两帧图像的角点位置图作为MagicWarp网络的输入,最终输出单应性矩阵。

MagicWarp输入是Image A和A经过单应性变换后生成的Image B,第一个Reshape就是变成了Magic Point的标准输出(可以回头去看看),然后将两个tensor通过cat在一起,再经过VGG来Encoding,通过两个全连接层输出9个数值,即3*3的单应性矩阵。
3.2、训练
训练就需要数据集。从上图可以看出,网络的输入是点位置图,或者叫点图,于是作者便设计了一种方式来采集:
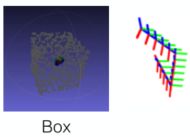
首先设计一个3D点云图,并设计一个相机采样的轨迹。让相机在轨迹上运动并拍照,就形成了一串连续帧。让任意两个有关联的帧组成一队都可以送入网络中训练。文中讲到他们至少随机抽取了30%有视觉重叠的图像对,并且在训练时,会随机丢弃一些点,以提高鲁棒性。发现随机丢弃50%的匹配点(整对丢弃?)和随机求其25%的独立点(只在一幅图中丢弃点?)效果很好。
3.3、损失函数
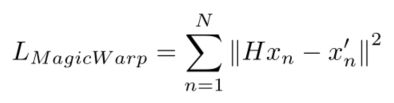
x n x_n xn:为帧图1
H H H:为帧图1变换到帧图2时单应性矩阵(相机的位姿变化)
x n ′ x^{'}_{n} xn′:为帧图2
也就是说如果网络预测的H和真实的H很接近,那么我将H作用于帧图1后得到的帧图2,和真实帧图2上的角点位置,应当是一样的,即角点位置的L2距离。
(启发点:如果我们自己实现通过帧间图像估计相机位姿的变化,那么如何估计我们估计的位姿 H H H和真实位姿之间 H g t H_{gt} Hgt测差距,一种想当然的方法是计算 H H H和 H g t H_{gt} Hgt的差距,但是事实上 H g t H_{gt} Hgt并不好测量,你需要知道相机的旋转和平移量。本文这里的评估则不需要 H g t H_{gt} Hgt,直接测量角点位置的差距,毕竟在一幅图上计算两个关键点的差是更容易一些的)
4、效果
4.1、MagicPoint效果
4.1.1、平均精度和定位误差
下图展示没有噪声的场景下,不同角点检测方法的平均精度

下图展示在有噪声的场景下,不同角点检测方法的平均精度

可见MagicPoint对噪声的鲁棒性很强
同样的,下图展示不同角点检测方法的角点定位误差(上图无噪声,下图有噪声)

4.1.2、不同噪声程度下的角点检测效果
既然展示了有噪声的因素,那么其效果随噪声的强度不同,有什么变化呢?
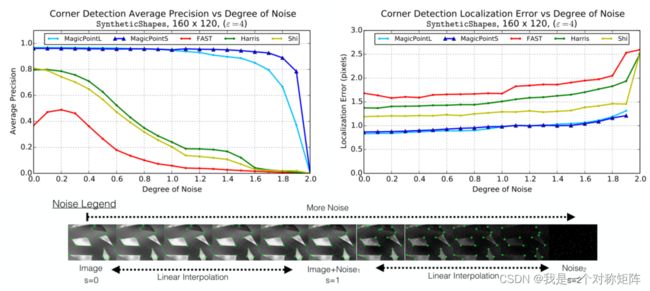
上图展示了不同随着噪声程度的加强,各种角点检测算法的表现。
4.1.3、不同噪声类型下的角点检测效果
4.1.4、不同静态场景下角点检测效果
先看要实验的4种场景共30副效果图
在这4种场景下,不同角点检测算法的表现如何呢?
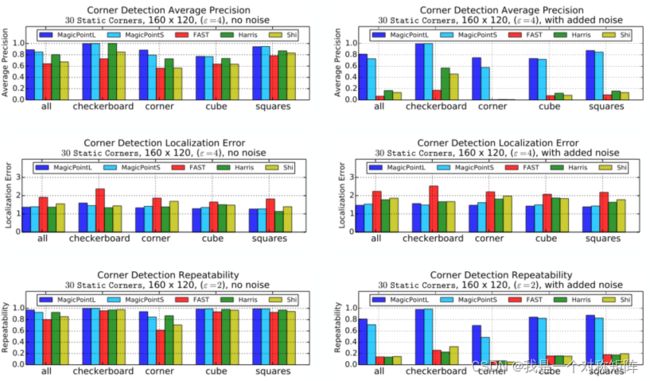
4.2、MagicWarp效果
4.2.1、MagicWarp的匹配能力
文中关于匹配能力的定义如下:
在图1中定义一个点集 x i x_i xi,其中 i ∈ { 1 , . . . , N 1 } i∈\{1,...,N_1\} i∈{1,...,N1},
在图2中定义一个点集 x j x_j xj,其中 j ∈ { 1 , . . . , N 2 } j∈\{1,...,N_2\} j∈{1,...,N2},
并定义ground truth转换矩阵 H ^ \hat{H} H^,和预测的转换矩阵 H H H
则:
M a t c h C o r r ( x i ) = MatchCorr(x_i)= MatchCorr(xi)=
a r g m i n j ∈ 1 , . . . , N 2 ∣ ∣ H x i ′ − x j ∣ ∣ = = H ^ x i ′ argmin_{j∈{1,...,N_2}}||Hx^{'}_i-x_j||==\hat{H}x^{'}_i argminj∈1,...,N2∣∣Hxi′−xj∣∣==H^xi′
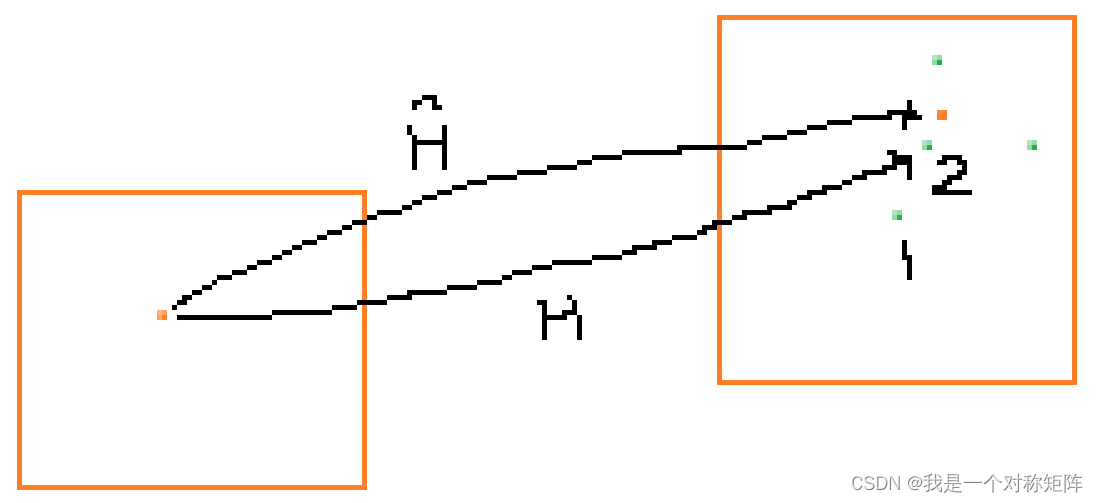
由公式可以看出,左边是将原坐标经预测的转换矩阵H转换后,找到距离自己最近的点作为匹配结果;右侧是将原坐标经gt转换矩阵H转换后的点。如果两个点一样,则证明预测矩阵H是接近gt矩阵H的。
如果 H H H和 H ^ \hat{H} H^一样,则应当将橙色点转换到橙色点,但是因为有误差,不可能完全一样,故转换后的点有偏差,但是偏差不大,我们仍认为是正确的。但是如果 H H H偏差过大,则转移后可能就映射到点1了,此时距离橙色点最近的是点2,则==不成立,故仍未匹配失败。
4.2.2、展示匹配效果

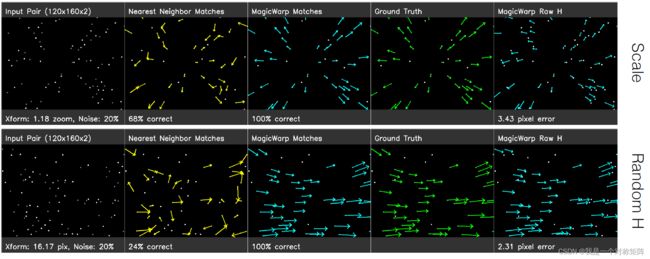
首先这里展示了Translation、Rotation、Scale、Random H四种变换的效果。
- 左侧是输入图,方法细看可以看到图中的点有亮点和灰点两种,灰点表示原图,亮点表示变换后的图。
- 绿色:表示gt匹配,就是真正正确的匹配对
- 黄色:表示最邻近方法找到的匹配点(从第一行就可以看出,明明是简单的平移,该算法·找到的匹配混乱)
- 蓝色:表示MagicWarp找到的匹配点,基本与绿色的绝对正确匹配一样
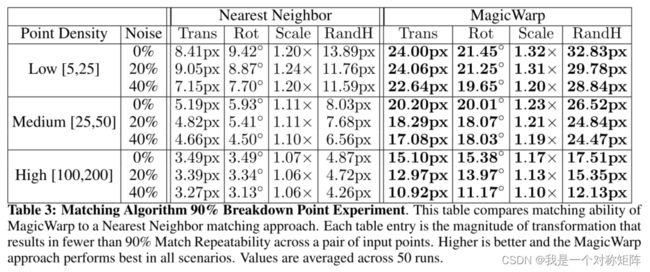
4.2.3、四种变换在不同强度下,MagicWarp的效果
分别展示了Translation、Rotation、Scale、Random H四种变换的效果,在不同强度下(比如平移更多,旋转更多,缩放比例更大等),匹配效果。
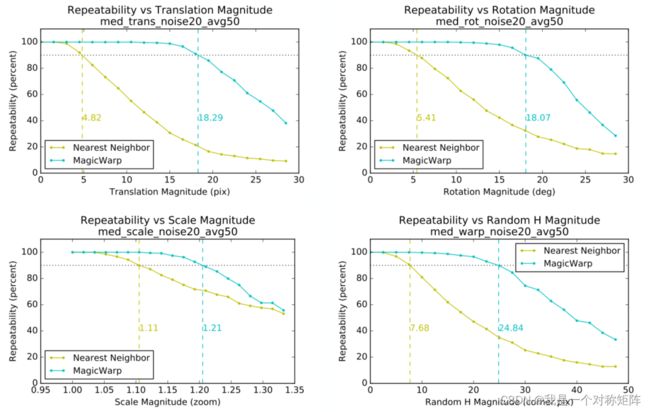
注意,为什么图中选择了90%这个节点,作者说:“We choose 90% because we believe that a robust geometric decomposition using the correspondences should be able to deal with 10% of incorrect matches. Unsurprisingly, the MagicWarp approach outperforms the Nearest Neighbor matching approach in all scenarios.”,大概就是说你连90%的精度都达不到,还好意思说自己的系统鲁棒?
4.3、附录展示MagicPoint的效果
每个场景共6张图,分别是:MagicPoint输出的可视化图;概率热力图;增强的概率分布热力图(通过log实现);其他三种角点检测算法的效果图;