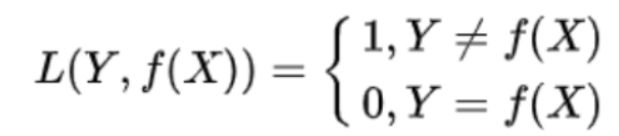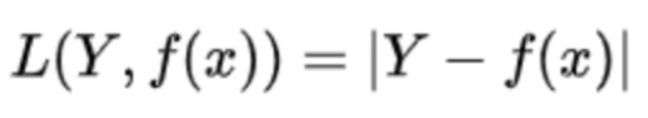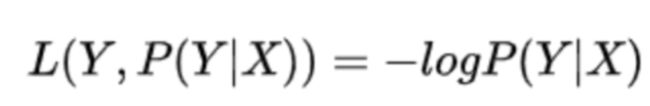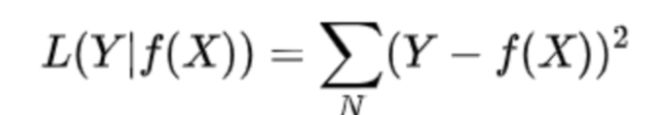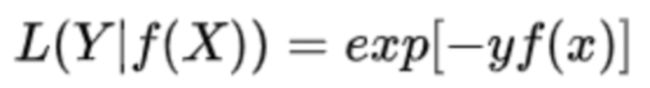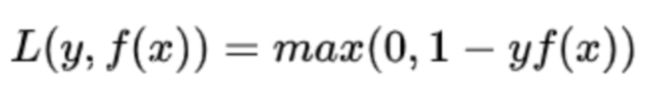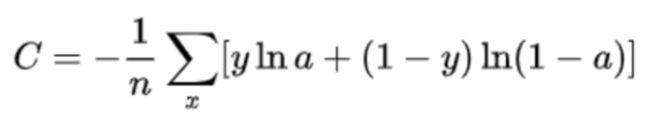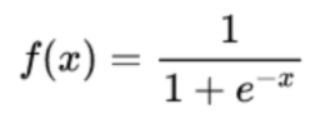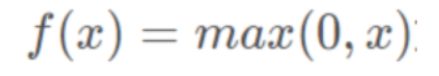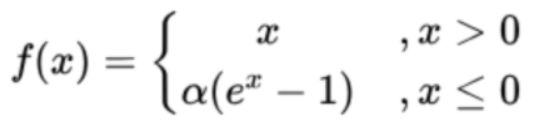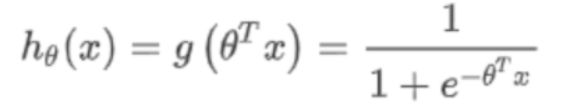2021年3月17日，机器学习算法岗实习岗面试题6道

问题1：常见的损失函数，常见的激活函数，ELU函数了解吗?

常见的损失函数：0-1损失函数，绝对值损失函数，log对数损失函数，平方损失函数，指数损失函数，hinge损失函数，交叉熵损失函数等。

0-1损失函数

绝对值损失函数

log对数损失函数

平方损失函数

指数损失函数

hinge损失函数

交叉熵损失函数

常见的激活函数有：Sigmoid、Tanh、ReLU、Leaky ReLU

Sigmoid函数：

特点：

它能够把输入的连续实值变换为0和1之间的输出，特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1。

缺点：

缺点1：在深度神经网络中梯度反向传递时导致梯度消失，其中梯度爆炸发生的概率非常小，而梯度消失发生的概率比较大。

缺点2：Sigmoid 的 output不是0均值（即zero-centered）。

缺点3：其解析式中含有幂运算，计算机求解时相对来讲比较耗时。对于规模比较大的深度网络，这会较大地增加训练时间。

Tanh函数：

特点：它解决了Sigmoid函数的不是zero-centered输出问题，收敛速度比sigmoid要快，然而，梯度消失（gradient vanishing）的问题和幂运算的问题仍然存在。

ReLU函数：

特点：

1.ReLu函数是利用阈值来进行因变量的输出，因此其计算复杂度会比剩下两个函数低（后两个函数都是进行指数运算）

2.ReLu函数的非饱和性可以有效地解决梯度消失的问题，提供相对宽的激活边界。

3.ReLU的单侧抑制提供了网络的稀疏表达能力。

ReLU的局限性:在于其训练过程中会导致神经元死亡的问题。

这是由于函数f(x)=max(0,x)导致负梯度在经过该ReLU单元时被置为0，且在之后也不被任何数据激活，即流经该神经元的梯度永远为0，不对任何数据产生响应。在实际训练中，如果学习率（Learning Rate）设置较大，会导致超过一定比例的神经元不可逆死亡，进而参数梯度无法更新，整个训练过程失败。

Leaky ReLu函数：

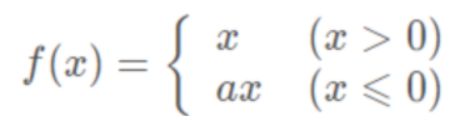
LReLU与ReLU的区别在于， 当z<0时其值不为0，而是一个斜率为a的线性函数，一般a为一个很小的正常数， 这样既实现了单侧抑制，又保留了部分负梯度信息以致不完全丢失。但另一方面，a值的选择增加了问题难度，需要较强的人工先验或多次重复训练以确定合适的参数值。

基于此，参数化的PReLU（Parametric ReLU）应运而生。它与LReLU的主要区别是将负轴部分斜率a作为网络中一个可学习的参数，进行反向传播训练，与其他含参数网络层联合优化。而另一个LReLU的变种增加了“随机化”机制，具体地，在训练过程中，斜率a作为一个满足某种分布的随机采样；测试时再固定下来。Random ReLU（RReLU）在一定程度上能起到正则化的作用。

ELU函数：

ELU函数是针对ReLU函数的一个改进型，相比于ReLU函数，在输入为负数的情况下，是有一定的输出的，而且这部分输出还具有一定的抗干扰能力。这样可以消除ReLU死掉的问题，不过还是有梯度饱和和指数运算的问题。

问题2：分类问题为什么不用MSE，而是要用交叉嫡。

LR的基本表达形式如下：

使用交叉熵作为损失函数的梯度下降更新求导的结果如下：

首先得到损失函数如下：

如果我们使用MSE作为损失函数的话，那损失函数以及求导的结果如下所示：

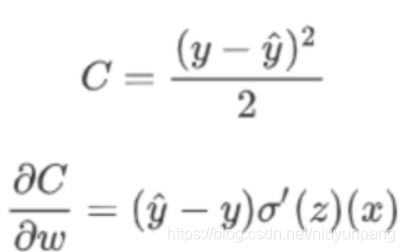
使用平方损失函数，会发现梯度更新的速度和sigmod函数本身的梯度是很相关的。sigmod函数在它在定义域内的梯度都不大于0.25。这样训练会非常的慢。使用交叉熵的话就不会出现这样的情况，它的导数就是一个差值，误差大的话更新的就快，误差小的话就更新的慢点，这正是我们想要的。

在使用 Sigmoid 函数作为正样本的概率时，同时将平方损失作为损失函数，这时所构造出来的损失函数是非凸的，不容易求解，容易得到其局部最优解。如果使用极大似然，其目标函数就是对数似然函数，该损失函数是关于未知参数的高阶连续可导的凸函数，便于求其全局最优解。（关于是否是凸函数，由凸函数的定义得，对于一元函数，其二阶导数总是非负，对于多元函数，其Hessian矩阵（Hessian矩阵是由多元函数的二阶导数组成的方阵）的正定性来判断。如果Hessian矩阵是半正定矩阵）

问题3：F1score的计算公式。

要计算F1score，首先要计算 Precision 和 Recall，公式如下：

问题4：FM vs SVM的比较

FM和SVM最大的不同，在于特征组合时权重的计算方法

SVM的二元特征交叉参数是独立的，而FM的二元特征交叉参数是两个k维的向量 v_i，v_j ，交叉参数不是独立的，而是互相影响的
FM可以在原始形式下进行优化学习，而基于kernel的非线性SVM通常需要在对偶形式下进行
FM的模型预测与训练样本独立，而SVM则与部分训练样本有关，即支持向量.
FM模型有两个优势：

在高度稀疏的情况下特征之间的交叉仍然能够估计，而且可以泛化到未被观察的交叉参数的学习和模型的预测的时间复杂度是线性的

问题5：随机森林的随机性

随机森林的随机性体现在每颗树的训练样本是随机的，树中每个节点的分裂属性集合也是随机选择确定的。有了这2个随机的保证，随机森林就不会产生过拟合的现象了。

问题6：编程题:跳跃游戏(leetcode55)

思路：贪心算法

依次遍历数组中的每一个位置，并实时维护最远可以到达的位置 rightMost，注意当前遍历到的位置 i 要在最远可以到达的位置范围内（也就是满足 i <= rightMost），当rightMost 大于或等于 数组最后一个位置时，就表示可以到达，返回 True，否则就要返回 False。

代码如下：

时间复杂度：O(n)，其中 n 为数组的大小。只需要访问 nums 数组一遍，共 n 个位置。

空间复杂度：O(1)，不需要额外的空间开销。

评论区回复 “121”，七月在线干货组最新升级的《2021大厂最新AI面试题 [含答案和解析, 更新到前121题]》，免费送！
持续无限期更新大厂最新面试题，AI干货资料，目前干货组汇总了今年3月-6月份，各大厂面试题。