神经网络(一)—— 单层感知机
感知机
介绍
感知机是一个二类分类的线性分类模型,用来做分类的,类别用+1和-1表示。
样本中的各个特征组成了空间中的不同的点,点被分成两类,+1和-1。我们的目的就是找到一个超平面将这两类点分开。超平面可以用wx+b表示,或者将b改写成 w 0 w_0 w0,将x的第一列加上偏置项(全1)。那么我们就可以用wx来表示这个超平面。将样本数据x代入,若所得wx>0,则说明该点在此超平面上方,<0则说明在此超平面下方。大于0时我们将输出值设置为1,小于0时我们将输出值设置为0。这个操作用数学来表达就是
f ( x ) = s i g n ( w x + b ) f(x)=sign(wx+b) f(x)=sign(wx+b)
s i g n ( x ) = { + 1 , x ≥ 0 − 1 , x < 0 sign(x)=\begin{cases} +1,x\geq0\\ -1,x<0 \end{cases} sign(x)={+1,x≥0−1,x<0
一开始的w是随便定的,所以我们要不断地调整w,以使得输出值与样本原有的分类值相同,这就代表我们成功地训练出了w。
当然这一切都有个前提,那就是我们的样本本身是线性可分的,也就是说我们可以用一个超平面将不同类别的数据点分隔在两边。
比如对于异或问题,单层感知机是不能解决的。如果你把(0,0),(0,1),(1,0),(1,1)四个点在坐标轴上画出来(其中00和11为1,01和10为-1),你就会发现无法画一条直线将两类点分开,因为他们线性不可分,单层感知机无法解决。
损失函数
我们不断修改w的值来修正输出值以符合原有类别,这个过程可以解释为不断减少误分类点的个数的过程。在空间中,点 x 0 x_0 x0到超平面 w x + b wx+b wx+b的距离有如下公式:
d = ∣ w x 0 + b ∣ ∣ ∣ w ∣ ∣ d = \frac{|wx_0+b|}{||w||} d=∣∣w∣∣∣wx0+b∣
我们假设 x 0 x_0 x0是一个误分类的点,那么公式就可以转化为:
d = − y 0 ( w x 0 + b ) ∣ ∣ w ∣ ∣ d=\frac{-y_0(wx_0+b)}{||w||} d=∣∣w∣∣−y0(wx0+b)
就是去个绝对值,因为 y 0 y_0 y0是取正负一。
假设所有误分类的点都在集合M中,那么所有误分类的点到超平面的距离之和就可以写成
− 1 ∣ ∣ w ∣ ∣ ∑ x i ∈ M y i ( w x i + b ) -\frac1{||w||}\sum_{x_i\in M} y_i(wx_i+b) −∣∣w∣∣1xi∈M∑yi(wxi+b)
我们就是要让这个值化为0,也就是说所有点都分对了。
于是损失函数就是这个
L ( w , b ) = − ∑ x i ∈ M y i ( w x i + b ) L(w,b)=-\sum_{x_i\in M} y_i(wx_i+b) L(w,b)=−xi∈M∑yi(wxi+b)
或者
L ( w ) = − ∑ x i ∈ M y i ( w x i ) L(w)=-\sum_{x_i\in M}y_i(wx_i) L(w)=−xi∈M∑yi(wxi)
梯度下降
我们对损失函数中的w求导可得
∇ L ( w ) = − ∑ x i ∈ M y i x i \nabla L(w)=-\sum_{x_i\in M}y_ix_i ∇L(w)=−xi∈M∑yixi
w的迭代函数就为
w : = w + η y x w:=w+\eta yx w:=w+ηyx
若我们将M扩展为所有点,则迭代公式还可以改写成
w : = w + η ( y − t ) x w:=w+\eta (y-t)x w:=w+η(y−t)x
其中 η \eta η代表学习率,t代表上一次的输出(分类)结果。
简单实现
# encoding:utf-8
import numpy as np
import matplotlib.pyplot as plt
# 输入数据
X = np.array([[1,3,3],
[1,4,3],
[1,1,1],
[1,0,2]])
Y = np.array([[1],
[1],
[-1],
[-1]])
# 权值初始化到-1~1
W = (np.random.random([3,1])-0.5)*2
# 学习率
lr = 0.1
# 临时输出
O = 0
# 更新权值
def update():
global X,Y,W,lr
O = np.sign(np.dot(X,W))
W_C = lr*(X.T.dot(Y-O))/X.shape[0]
W = W + W_C
# 迭代
for i in range(100):
update()
O = np.sign(np.dot(X,W))
if(O == Y).all():
break
# 正样本
x1 = [3,4]
y1 = [3,3]
# 负样本
x2 = [1,0]
y2 = [1,2]
# 计算斜率和截距
k = -W[1]/W[2]
b = -W[0]/W[2]
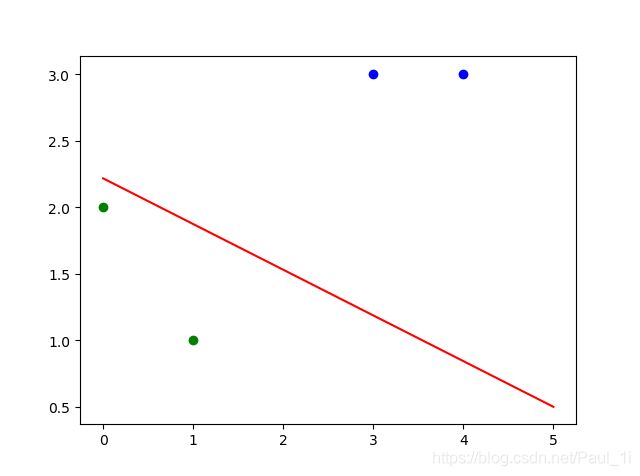
plt.scatter(x1,y1,c='b')
plt.scatter(x2,y2,c='g')
xdata = (0,5)
plt.plot(xdata,k*xdata+b,'r')
plt.show()