量子通讯加密技术的技术原理

1 什么是量子

一个物理量如果存在最小的不可分割的基本单位，则这个物理量是量子化的，并把最小单位称为量子。量子英文名称量子一词来自拉丁语quantus，意为“有多少”，代表“相当数量的某物质”。在物理学中常用到量子的概念，指一个不可分割的基本个体。例如，“光的量子”（光子）是一定频率的光的基本能量单位。而延伸出的量子力学、量子光学等成为不同的专业研究领域。其基本概念为所有的有形性质是“可量子化的”。“量子化”指其物理量的数值是离散的，而不是连续地任意取值。例如，在原子中，电子的能量是可量子化的。这决定了原子的稳定性和发射光谱等一般问题。绝大多数物理学家将量子力学视为了解和描述自然的的基本理论。
通俗地说，量子是能表现出某物质或物理量特性的最小单元。

2 什么是量子叠加态

量子作为不可再分割的基本个体，用来形容微观世界的一种倾向，物质或粒子的能力都倾向于不连续的变化，其事物不是明确的非此即彼，而是此与彼的某种尚未确定的叠加态。
举个例子，A要从德国柏林飞到中国北京，飞机有两种飞行路线，一种是柏林中转莫斯科到北京，一种是柏林中转新加坡到北京，如果A在飞机上睡着了，那么他不知道飞机到底是从莫斯科中转到还是从新加坡中转，这时用量子力学的观点就会说我现在同时在莫斯科和新加坡，也就是量子的叠加态，而当潘教授郑看眼睛看的时候她才知道到底是从莫斯科中转还是从新加坡中转，这也是量子力学的积极哲学，看到即改变。当你把视线关注到量子的运动轨迹，其状态就会随之发生。

3 什么是量子纠缠

以双粒子为例，一个粒子A可以处于某个物理量的叠加态，用一个量子比特来表示，同时另一个粒子B也可以处于叠加态。当两个粒子发生纠缠，就会形成一个双粒子的叠加态，即纠缠态。例如有一种纠缠态就是无论两个粒子相隔多远，只要没有外界干扰，当A粒子处于0态时，B粒子一定处于1态；反之，当A粒子处于1态时，B粒子一定处于0态。
　用薛定谔的猫做比喻，就是A和B两只猫如果形成上面的纠缠态：

无论两只猫相距多远，即便在宇宙的两端，当A猫是“死”的时候，B猫必然是“活”；当A猫是“活”的时候，B猫一定是“死”(当然真实的情况是猫这种宏观物体不可能把量子纠缠维持这么长时间，几亿亿亿亿分之一秒内就会解除纠缠。但是基本粒子是可以的，比如光子。)。
　　这种跨越空间的、瞬间影响双方的量子纠缠曾经被爱因斯坦称为“鬼魅的超距作用”(spooky action at a distance)，并以此来质疑量子力学的完备性，因为这个超距作用违反了他提出的“定域性”原理，即任何空间上相互影响的速度都不能超过光速。这就是著名的“EPR佯谬”(编者注：EPR是三位物理学家姓氏的首字母缩写，其中，E是爱因斯坦，P是波多尔斯基，R是罗森，1935年，他们三人为论证量子力学的不完备性而提出了该佯谬)。
　　后来物理学家玻姆在爱因斯坦的定域性原理基础上，提出了“隐变量理论”来解释这种超距相互作用。
　　不久物理学家贝尔提出了一个不等式，可以来判定量子力学和隐变量理论谁正确。如果实验结果符合贝尔不等式，则隐变量理论胜出。如果实验结果违反了贝尔不等式，则量子力学胜出。
　　

贝尔不等式的意义

但是后来一次次实验结果都违反了贝尔不等式，即都证实了量子力学是对的，量子纠缠是非定域的，而隐变量理论是错的，爱因斯坦的定域性原理必须被舍弃。
　　2015年，荷兰物理学家做的最新的无漏洞贝尔不等式测量实验，基本宣告了定域性原理的死刑。
　　一些新的理论研究指出，微观上的量子纠缠与宏观的热力学第二定律，即熵增定律有着密不可分的关系。微观系统产生的纠缠具有不可逆性，会导致信息的增加(例如一个量子比特所含的信息是零个比特，但是两个量子比特纠缠在一起，就会产生两个比特的冗余信息)。
　　根据香农提出的信息论，系统熵正比于冗余的信息(即无用的信息)，因此宏观系统熵的增加，其根源很可能就来自微观的量子纠缠。
　　随着量子信息学的诞生，量子纠缠已经不仅仅是一个基础研究，它已经成为了量子信息科技的核心：例如利用量子纠缠可以完成量子通信中的量子隐形传态，可以完成一次性操作多个量子比特的量子计算。让更多的粒子纠缠起来是量子信息科技不断追寻的目标。

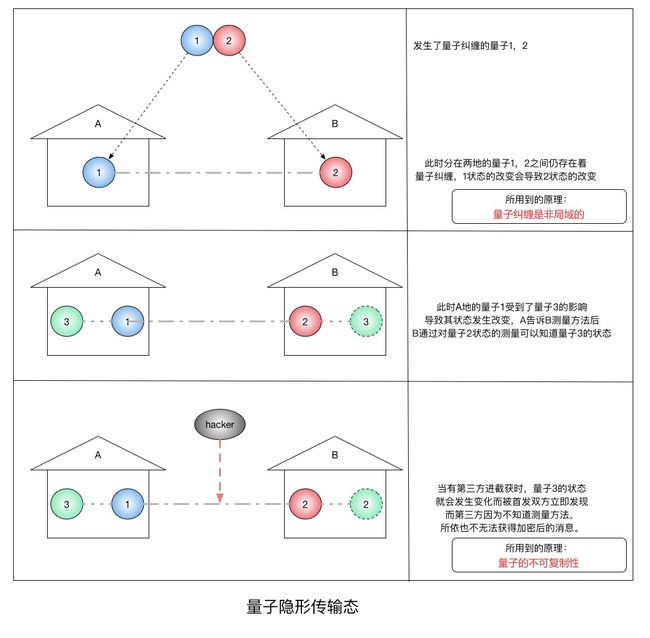
4 量子隐形传态

理解了量子纠缠，我们就可以理解量子隐形传态了。
　　由于量子纠缠是非局域的，即两个纠缠的粒子无论相距多远，测量其中一个的状态必然能同时获得另一个粒子的状态，这个“信息”的获取是不受光速限制的。于是，物理学家自然想到了是否能把这种跨越空间的纠缠态用来进行信息传输
因此，基于量子纠缠态的量子通讯便应运而生，这种利用量子纠缠态的量子通讯就是“量子隐形传态”(quantum teleportation)。
　　虽然借用了科幻小说中隐形传态(teleportation)这个词，但量子隐形传态实际上和科幻中的隐形传态关系并不大，它是通过跨越空间的量子纠缠来实现对量子比特的传输。
通俗地讲就是A，B两地各有一个相互纠缠的量子1，2，根据量子纠缠定理可知，当量子1的状态发生改变，量子2的状态也会发生改变。在A地有一个新的量子3包含了想要传输的量子比特Q，当A地的1，3量子在一起的时候会将1量子的状态改变，这个时候B地通过2量子状态的改变知道了可以知道A地1量子发生了改变，这时A地将测量方法告诉B地，B通过测量方法对2量子进行测量后就可以得到3量子在测量前的状态，也就得到了想要知道的量子比特Q。也就是粒子3携带的量子比特无损地从A点传输到了B点，而粒子3本身只留在A点，并没有到B点。

量子隐形传态的过程(即传输协议)一般分如下几步：

• (1) 制备一个纠缠粒子对。将粒子1发射到A点，粒子2发送至B点。
• (2) 在A点，另一个粒子3携带一个想要传输的量子比特Q。于是A点的粒子1和B点的粒子2对于粒子3一起会形成一个总的态。在A点同时测量粒子1和粒子3，得到一个测量结果。这个测量会使粒子1和粒子2的纠缠态坍缩掉，但同时粒子1和和粒子3却纠缠到了一起。
• (3) A点的一方利用经典信道(就是经典通讯方式，如电话或短信等)把自己的测量结果告诉B点一方。
• (4) B点的一方收到A点的测量结果后，就知道了B点的粒子2处于哪个态。只要对粒子2稍做一个简单的操作，它就会变成粒子3在测量前的状态。也就是粒子3携带的量子比特无损地从A点传输到了B点，而粒子3本身只留在A点，并没有到B点。
  需要注意的是，由于步骤3是经典信息传输而且不可忽略，因此它限制了整个量子隐形传态的速度，使得量子隐形传态的信息传输速度无法超过光速。

因为量子计算需要直接处理量子比特，于是“量子隐形传态”这种直接传的量子比特传输将成为未来量子计算之间的量子通信方式，未来量子隐形传态和量子计算机终端可以构成纯粹的量子信息传输和处理系统，即量子互联网。这也将是未来量子信息时代最显著的标志。

5 量子比特

在上文中提到的量子比特是什么呢？我们接下来一探究竟。
　　传统的信息技术扎根于经典物理学，一个比特在特定时刻只有特定的状态，要么0，要么1，所有的计算都按照经典的物理学规律进行。
量子信息扎根于量子物理学，一个量子比特(qubit)就是0和1的叠加态。相比于一个经典比特只有0和1两个值，一个量子比特的值有无限个。直观来看就是把0和1当成两个向量，一个量子比特可以是0和1这两个向量的所有可能的组合。

量子比特的Bloch球，球面代表了一个量子比特所有可能的取值。

但是需要指出的是，一个量子比特只含有零个经典比特的信息。因为一个经典比特是0或1，即两个向量。而一个量子比特只是一个向量(0和1的向量合成)，就好比一个经典比特只能取0，或者只能取1，信息量是零个比特。
其中，“量子密钥”使用量子态不可克隆的特性来产生二进制密码，为经典比特建立牢不可破的量子保密通信。

6 量子的不可克隆性

复制(即克隆)任何一个粒子的状态前，首先都要测量这个状态。但是量子态不同于经典状态，它非常脆弱，任何测量都会改变量子态本身(即令量子态坍缩)，因此量子态无法被任意克隆。这就是量子不可克隆定理，已经经过了数学上严格的证明。
　　窃听者在窃听经典信息的时候，等于复制了这份经典信息，使信息的原本接收者和窃听者各获得一份。但是在量子态传输时，因为无法克隆任意量子态，于是在窃听者窃听拦截量子通讯的时候，就会销毁他所截获到的这个量子态。
　　在量子密码里(如BB84协议)，正是由于量子不可克隆定理，光子被截获时经过了测量，偏振状态就发生了改变。接收方就会察觉密码的错误，停止密码通信。这也就确保了通信时量子密码的安全性，从而也就保证了加密信息的安全性。
　　在传输量子比特时，由于量子不可克隆定理，销毁量子态就是销毁了它所携带的量子比特，于是无论是接收者还是窃听者都无法再获得这个信息。通讯双方会轻易察觉信息的丢失，因此量子比特本身具有绝对的保密性。量子不可克隆定理使得我们直接传输量子比特的时候，不用再建立量子密码，而是直接依靠量子比特本身的安全性就可以做到信息不被窃取。
　　目前量子保密通信已经步入产业化阶段，开始保护我们的信息安全；“量子隐形传态”是利用量子纠缠来直接传输量子比特，它还处于基础研究阶段，未来将应用于量子计算机之间的直接通信。

7 量子秘钥

目前实用化的量子密钥分配是由查理斯。本内特(Charles Bennett)和吉勒。布拉萨(Gilles Brassard)在1984年提出的BB84协议。
　　该协议把密码以密钥的形式分配给信息的收发双方，因此也称作“量子密码”。该协议利用光子的偏振态来传输信息。因为光子有两个偏振方向，而且相互垂直，所以信息的发送者和接收者都可以简单地选取90度的测量方式，即“+”；或45度的测量方式，即“×”，来测量光子。在90度的测量方式中，偏振方向“↑”代表0，偏振方向“→”代表1；在45度的测量方式中，偏振方向“↗”代表0，偏振方向“↘”代表1。
　　这样选择测量方式的好处是，如果选择“+”来测量偏振态“↗”或“↘”时，会得到50%的几率为“→”，50%的几率为“↑”。同理，如果选择“×”来测量“→”或“↑”时，会得到50%的几率为“↗”，50%的几率为 “↘”。
　　为了生成一组二进制密钥，发送者首先随机生成一组二进制比特，我们称之为“发送者的密钥比特”。同时发送者对每个“发送者的密码比特”都随机选取一个测量模式(“+”或者“×”)，然后把在这个测量模式下，每个“发送者的密码比特”所对应的偏振状态的光子发送给接受者。比如传输一个比特0，选择的测量模式为+，则发送者需要发出一个偏振态为↑的光子。
　　接收者这边也对接收到的每个比特随机选择“+”或者“×”来测量，会测量出一组0和1。当接收者获得全部测量结果后，他要和发送者之间通过经典信道(如电话，短信，QQ等等)建立联系，互相分享各自用过的测量方式。这时他们只保留相同的测量方式(“+”或者“×”)，舍弃不同的测量方式。于是保留下来的测量方式所对应的二进制比特，就是他们最终生成的密码，如下表。

　　
　　通过上表我们可以看出，只有当发送方和接收方所选择的测量方式相同的时候，传输比特才能被保留下来用作密钥。
　　如果存在信息截获者，他也同样要随机地选取“+”或者“×”来测量发送者发送的比特。
　　例如，发送者选取测量方式“+”，然后发送“→”来代表1。如果截获者选取的也是“+”，他的截获就不会被察觉。但是因为截获者是随机选取的测量方式，他也有50%的概率选择“×”，于是量子力学的测量概率特性使光子的偏振就变为了50%的概率“↗”和50%的概率“↘”。
　　在上面的这种情况下，作为接收方如果选取了和发送方同样的测量方式“+”，则把这个比特当做密码。但是接收方测量的是经过截获的光子，即光子的偏振因为测量已经坍缩成了50%的概率↗和50%的概率↘，接收方测量最终结果无论如何都会变为50%的概率↑和50%的概率→。于是测量这个光子偏振的时候，发送方和接收方结果不同的概率为

50%×50%=25%。

因此想知道是否存在截获者，发送方和接收方只需要拿出一小部分密钥来对照。如果发现互相有25%的不同，那么就可以断定信息被截获了。同理，如果信息未被截获，那么二者密码的相同率是100%。于是BB84协议可以有效发现窃听，从而关闭通信，或重新分配密钥，直到没人窃听为止。
　　BB84量子密钥分配协议使得通讯双方可以生成一串绝对保密的量子密钥，用该密钥给任何二进制信息加密(比如做最简单的二进制“异或”操作，见表3)都会使加密后的二进制信息无法被解密，因此从根本上保证了传输信息过程的安全性。在这个协议基础上，世界各国都开展了传输用量子密钥加密过的二进制信息的网络建设，即量子保密通信网。中国在这方面走在了世界最前面。

利用量子密钥给需要传输的原始信息做“异或”加密

8 量子秘钥和量子隐形传输态的关系

我们可以用量子密钥给经典二进制信息加密。但是当我们需要传输量子比特时，就无法再使用量子密钥了，而需要使用“量子隐形传态”。

9 量子秘钥技术能保证数据的绝对安全吗？

我认为答案当然是否定的。世界上没有绝对的安全，就安全而言，除了传输过程中的安全外，还包括接受双方终端的安全，量子秘钥技术只能保证数据传输的安全性，但无法保证在数据存储，数据处理，甚至人为的破坏或者暴露！除此之外因为交换测量方法用的是传统通信方式，所以也是有可能被截获的，通过截获的测量方式可以翻译出来在被发现之前截获的消息。
也就是说量子秘钥技术只能保证数据传输过程的安全性，对其他方面的安全性仍无法保证！

参考文献

独家揭秘：量子通信如何做到“绝对安全”？
《开讲啦》 20160306 潘建伟：探索的动机
量子－百度百科