机器学习笔记——逻辑斯蒂回归(Logistic)
1.线性回归
1.1线性回归概念
如果特征值之间存在线性关系就可以使用线性回归建模对其预测结果。
![]()
1.2最小二乘法求解
何为最小二乘法,我们有很多的给定点,这时候我们需要找出一条线去拟合它,那么我先假设这个线的方程,然后把数据点代入假设的方程得到观测值,求使得实际值与观测值相减的平方和最小的参数。对变量求偏导联立便可求。
1.3 最大似然估计概念
举个例子,在有一组样本X1,X2,X3,…,Xn;取值x1,x2,…,xn。我们不知道这些样本所属总体服从的具体分布,但是我们知道他们和未知参数结合的形式——比如上述样本的概率分别为p(x1,θ1,θ2,…,θn),p(x2,θ1,θ2,…,θn),…,p(xn,θ1,θ2,…,θn). 那么现在如何对未知的参数θ1,θ2,…,θn进行估计以确定样本的函数?
那就是将这些样本对应的分布乘起来构建似然函数,再通过对似然函数求极大值,获得各个参数的取值。
![]()
这些已经出现的样本——我们有理由认为这些已经出现的样本值的概率更大。因此他们的联合分布的极大值得到的参数θ1,θ2,…,θn也是最贴近总体分布中的参数的。
2.逻辑斯蒂回归
逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降来求解参数,来达到将数据二分类的目的。
2.1sigmoid函数概念
逻辑斯蒂回归是一个经典的二分类模型,它的精髓在于用线性回归做二分类(或多分类,本文以二分类为主)。线性回归的输出为没有约束的连续值,而分类在于0和1两个值,如何从回归值到分类值就需要一个映射,于是引入了sigmoid函数: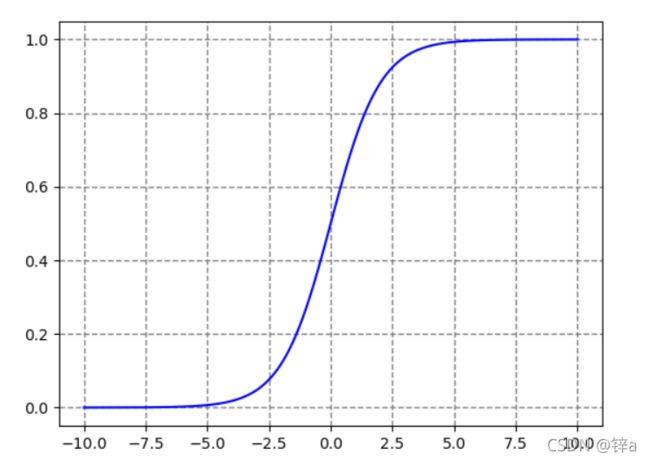
从图中可以看出,除了中间一小部分摸棱两可的,其余点都极大接近于1或0,可以把一个回归问题通过阀值进行二分类。
![]()
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(z):
return 1.0/(1.0+np.exp(-z))
z=np.arange(-6,6,0.05)
plt.plot(z,sigmoid(z))
plt.axvline(0.0,color='k')
plt.axhline(y=0.0,ls='dotted',color='k')
plt.axhline(y=1.0,ls='dotted',color='k')
plt.axhline(y=0.5,ls='dotted',color='k')
plt.yticks([0.0,0.5,1.0])
plt.ylim(-0.1,1.1)
plt.xlabel('z')
plt.ylabel('$\phi (z)$')
plt.show()2.2 二项逻辑斯蒂回归模型
首先我们来看最简单的二项logstic regression模型,它是由条件概率分布来表示,即:
![]()
此处引入几个简单的数学概念:
![]()
可以看到,Y=1的对数几率是输入x的线性函数,同时我们看到:
![]()
即输出Y的取值概率是由输入x的线性函数决定的的,回归也就体现在这里。
原文链接:https://blog.csdn.net/daaikuaichuan/article/details/80848958
2.3逻辑斯蒂模型求解
如何求解,那就需要用到最大似然估计了。
![]()
3.代码实现
3.1 使用梯度上升找到最佳参数
def loadDataSet():
dataMat = []; labelMat = []
fr = open('dataset5.txt')
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat,labelMat
def sigmoid(inX):
return 1.0/(1+exp(-inX))
def gradAscent(dataMatIn, classLabels):
#转换为numpy矩阵类型,便于优化和并行计算
dataMatrix = mat(dataMatIn) #convert to NumPy matrix
labelMat = mat(classLabels).transpose() #convert to NumPy matrix
#将Label转置为列向量
m,n = shape(dataMatrix)#m行n列
alpha = 0.001#学习速度
maxCycles = 500#最大学习步数
weights = ones((n,1))#将来的输出
for k in range(maxCycles): #heavy on matrix operations
h = sigmoid(dataMatrix*weights) #matrix mult
error = (labelMat - h) #vector subtraction
weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
return weights我们的目的就是要对这个似然函数的极大值进行参数估计,这便是我们训练Logistic回归模型的过程。通过极大似然估计我们便可以通过所有样本得到满足训练数据集的最合理的参数 w
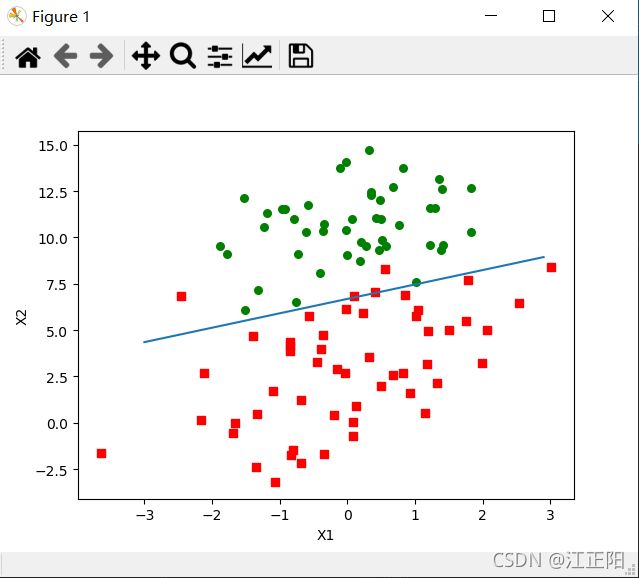
3.2 画出决策边界
这一段是就是想要画一条直线出来,但是只能画点,由点组成线
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat,labelMat=loadDataSet()#加载源数据,用于画图
dataArr = array(dataMat)#将data向量化
n = shape(dataArr)[0] #n为data的个数
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
#给data分类
for i in range(n):
if int(labelMat[i])== 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
#用不同的颜色画出来
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
#arange([start,] stop[, step,], dtype=None)
#根据start与stop指定的范围以及step设定的步长,生成一个 ndarray。
x = arange(-3.0, 3.0, 0.1)
y = (-weights[0]-weights[1]*x)/weights[2]
ax.plot(x, y)
plt.xlabel('X1'); plt.ylabel('X2');
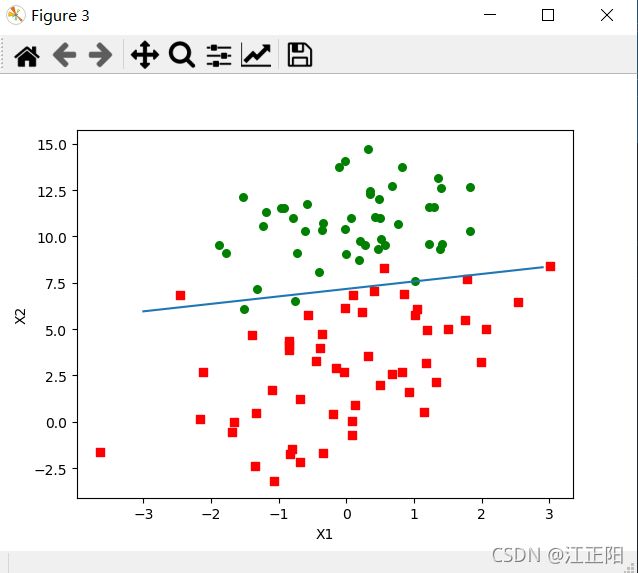
plt.show()3.3 随机梯度下降
这是只对整个数据集迭代了一次。
def stocGradAscent0(dataMatrix, classLabels):
m,n = shape(dataMatrix)
alpha = 0.01
weights = ones(n) #initialize to all ones
for i in range(m):
h = sigmoid(sum(dataMatrix[i]*weights))
error = classLabels[i] - h
#这里其实不是真正的随机,样本是按顺序取的
weights = weights + alpha * error * dataMatrix[i]
return weights很明显仅仅迭代一次效果并不好
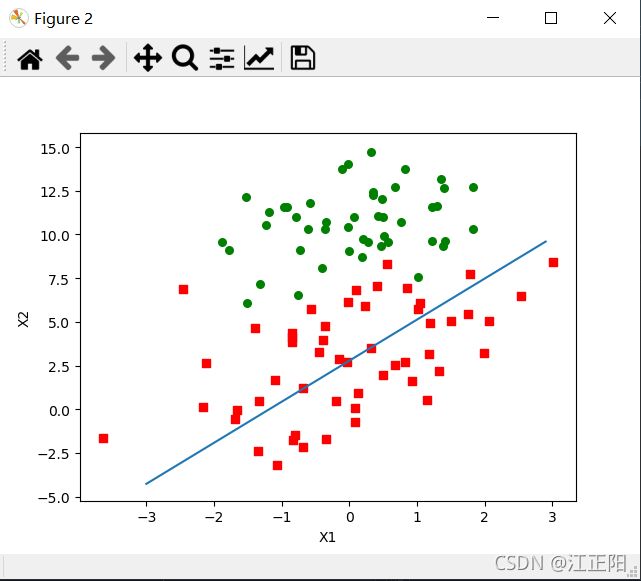
3.4 改进的随机梯度下降法
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m,n = shape(dataMatrix)
weights = ones(n) #initialize to all ones
for j in range(numIter):#对样本迭代150次
dataIndex = list(range(m))#dataIndex保存了所有在本次迭代中还没有使用过的data
for i in range(m):
alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not
print(alpha)
randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant
h = sigmoid(sum(dataMatrix[randIndex]*weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del(dataIndex[randIndex])
return weights改进:
- 学不仅进行了150次的迭代,学习速度在每次迭代后都会调整,越往后学习速度越小,这会缓解在最优点附近的波动.在alpha之后加了一个常数,这使得alpha即使再迭代也不会减小到0.在降低alpha的函数中,j是迭代次数,i是data下标,这样可以避免参数的严格下降
- 随机选择用来计算的data,上一种并不是真正的随机,是顺序取的,存在一些不能正确分类的样本点,导致系数波动,改进后的算法随机从列表中选取一个值,再从列表中删除
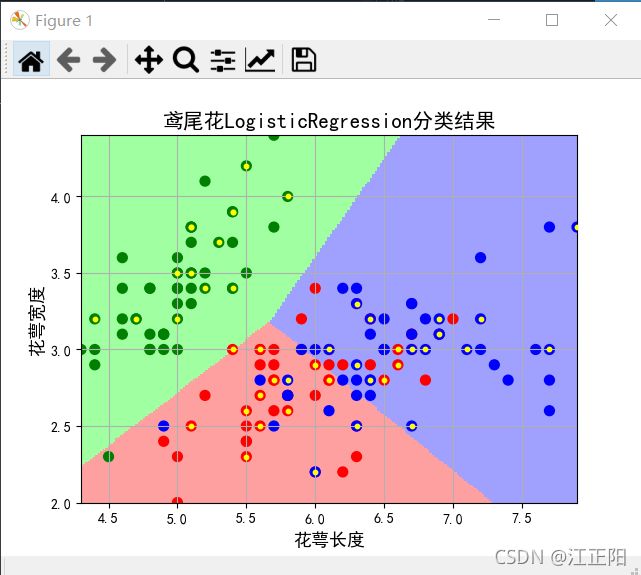
4.sklearn实现鸢尾花分类(skearn的LogisticRegression)
from sklearn.linear_model import LogisticRegression
import numpy as np
from sklearn import model_selection
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
# 定义一个函数,将不同类别标签与数字相对应
def iris_type(s):
class_label={b'Iris-setosa':0,b'Iris-versicolor':1,b'Iris-virginica':2}
return class_label[s]
#使用numpy中的loadtxt读入数据文件
filepath='iris/iris1.txt' # 数据文件路径
data=np.loadtxt(filepath,dtype=float,delimiter='\t',converters={4:iris_type})
'''
converters={4:iris_type} :对某一列数据(第四列)进行某种类型的转换,将数据列与转换函数进行映射的字典。eg:{1:fun},含义是将第2列对应转换函数进行转换。
'''
#将原始数据集划分成训练集和测试集
X ,y=np.split(data,(4,),axis=1) #np.split 按照列(axis=1)进行分割,从第四列开始往后的作为y 数据,之前的作为X 数据。函数 split(数据,分割位置,轴=1(水平分割) or 0(垂直分割))。
x=X[:,0:2] #在 X中取前两列作为特征(为了后期的可视化画图更加直观,故只取前两列特征值向量进行训练)
x_train,x_test,y_train,y_test=model_selection.train_test_split(x,y,random_state=1,test_size=0.3)
'''
用train_test_split将数据随机分为训练集和测试集,测试集占总数据的30%(test_size=0.3),random_state是随机数种子
x:train_data:所要划分的样本特征集。
y:train_target:所要划分的样本结果。
test_size:样本占比,如果是整数的话就是样本的数量。
random_state:是随机数的种子。
随机数种子:其实就是该组随机数的编号,在需要重复试验的时候,保证得到一组一样的随机数。比如你每次都填1,其他参数一样的情况下你得到的随机数组是一样的。但填0或不填,每次都会不一样。
随机数的产生取决于种子,随机数和种子之间的关系遵从以下两个规则:种子不同,产生不同的随机数;种子相同,即使实例不同也产生相同的随机数。)
'''
#搭建模型,训练LogisticRegression分类器
classifier=Pipeline([('sc',StandardScaler()),('clf',LogisticRegression())])
#开始训练
classifier.fit(x_train,y_train.ravel())
def show_accuracy(y_hat,y_test,parameter):
pass
#计算LogisticRegression分类器的准确率
print("LogisticRegression-输出训练集的准确率为:",classifier.score(x_train,y_train))
y_hat=classifier.predict(x_train)
show_accuracy(y_hat,y_train,'训练集')
print("LogisticRegression-输出测试集的准确率为:",classifier.score(x_test,y_test))
y_hat=classifier.predict(x_test)
show_accuracy(y_hat,y_test,'测试集')
# 绘制图像
# 1.确定坐标轴范围,x,y轴分别表示两个特征
x1_min, x1_max = x[:, 0].min(), x[:, 0].max() # 第0列的范围
x2_min, x2_max = x[:, 1].min(), x[:, 1].max() # 第1列的范围
x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j] # 生成网格采样点
grid_test = np.stack((x1.flat, x2.flat), axis=1) # 测试点
# print 'grid_test = \n', grid_test
grid_hat = classifier.predict(grid_test) # 预测分类值
grid_hat = grid_hat.reshape(x1.shape) # 使之与输入的形状相同
# 2.指定默认字体
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
# 3.绘制
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
alpha=0.5
plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light) # 预测值grid_hat的显示 显示分类区域
plt.scatter(x[:, 0], x[:, 1], c=y.ravel(),s=50, cmap=cm_dark) # 样本
plt.scatter(x_test[:, 0], x_test[:, 1], s=10, facecolors='yellow', zorder=3) # 圈中测试集样本
plt.xlabel(u'花萼长度', fontsize=13)
plt.ylabel(u'花萼宽度', fontsize=13)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.title(u'鸢尾花LogisticRegression分类结果', fontsize=15)
plt.grid() #显示网格
plt.show()