数学建模那些事儿

小羊简介：

---

博客主页：小羊不会飞

年龄：20    大二在读   

爱好：干饭，运动，码代码，看书，旅游

即将更新：

1、手把手带你搭建个人博客网站

2、后台管理系统模块更新

：感兴趣的朋友，赶紧上车吧！！

欢迎关注点赞收藏留言

有任何疑问，欢迎留言讨论！！！

---

目录

什么，是数学建模？

新手不知道的小知识

1、建模三条大腿

2、建模三大工具

3、建模干货

4、集训日程表

建模常见的一些问题

1、预测

2、优化

3、评价

关于第一次比赛后的个人体会

---

什么，是数学建模？

由于博主只参加过高教社杯全国大学生数学建模竞赛（CUMCM），所以下面就重点介绍一下这个比赛，像其他类似的建模比赛还有MCM/ICM美国大学数学建模竞赛，华为杯中国研究生数学建模竞赛....

1.高教社杯全国大学生数学建模竞赛（CUMCM）

该竞赛创办于1992年，每年一届，是首批列入“高校学科竞赛排行榜”的19项竞赛之一。2021年，来自全国及美国、马来西亚等国家的1566所院校/校区、49529队(本科45075队、专科4454队)、14万多人报名参赛。

报名时间：报名截止时间九月之前，各个高校会统一组织报名，时间大概在七八月份

集训时间：一般是一整个暑假（因学校安排而异）

比赛时间：9月中旬

含金量:因为纳入高校学科竞赛排行榜，所以认可度最高，俗称国赛。

竞赛官网：全国大学生数学建模竞赛

报名费：300元（一般学校都会给予报销）

新手不知道的小知识

1、建模三条大腿

建模手

建模手主要是找方法选手，外交选手，数据收集与整理选手，敲公式选手。寻找最佳解答问题模型并搭建（前期确定方法需要三个队友一起决定，因为此时编程还未开始，写作也不慌动笔）

编程手

编程手主要负责导数据处理数据，写代码，解决bug，计算结果，整理结果，绘制图表，分析数据特征，分析结果。

论文手

论文手，格式规范者（我们当时队伍里的学姐会用Latex，写出来的文章格式就非常nice），文章脉络完善者，逻辑自圆其说者，提出要求者，比赛规则清晰者，细节处理者。

2、建模三大工具

lingo（主要用来解决一些规划问题）

spss（主要用来做一些数据分析）

matlab（别问，问就是什么东西都可以做，除了生孩子）

3、建模干货

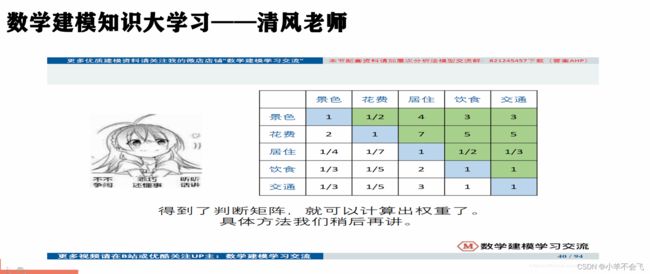
划重点： 博主在此非常感谢清风老师，很多算法和知识都是从清风老师这儿学的，非常感谢！！！

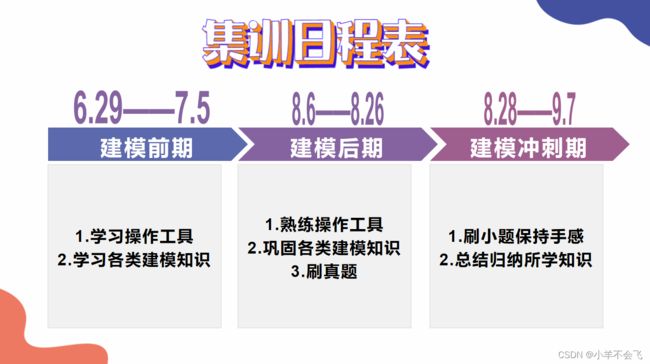
4、集训日程表

 

建模常见的一些问题

1、预测

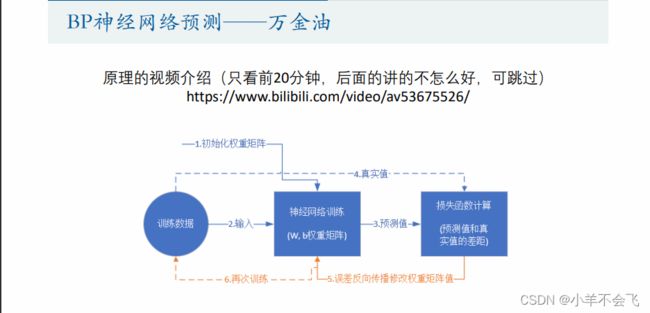
✨ 这个是博主在收到学校老师邀请参见建模宣讲会时做的一个关于预测模型的小结

（希望对大家有帮助）

 ✨博主当时主要学的是BP神经网络预测，并且在最后的国赛C题的第一个小问中也成功应用到了该方法（上图是我们国赛论文的一部分），最后只能说BPyyds

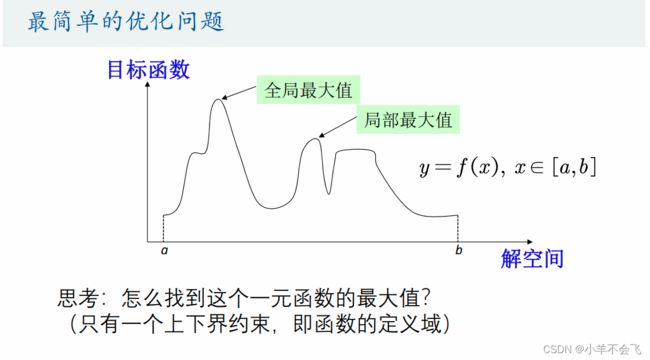
2、优化

说到优化，说白了就是求一个最值吧，但实际问题中我们很难得到全局最优解，很多情况下只能得到局部最优解，这个时候就不得不提一下那些晦涩难懂的优化算法了，像什么蚁群算法，模拟退火算法，遗传算法，粒子群算法......

 

%% 粒子群算法PSO: 求解函数y = 11*sin(x) + 7*cos(5*x)在[-3,3]内的最大值(动画演示）
clear; clc

%% 绘制函数的图形
x = -3:0.01:3;
y = 11*sin(x) + 7*cos(5*x);
figure(1)
plot(x,y,'b-')
title('y = 11*sin(x) + 7*cos(5*x)')
hold on  % 不关闭图形，继续在上面画图

%% 粒子群算法中的预设参数（参数的设置不是固定的，可以适当修改）
n = 10; % 粒子数量
narvs = 1; % 变量个数
c1 = 2;  % 每个粒子的个体学习因子，也称为个体加速常数
c2 = 2;  % 每个粒子的社会学习因子，也称为社会加速常数
w = 0.9;  % 惯性权重
K = 50;  % 迭代的次数
vmax = 1.2; % 粒子的最大速度
x_lb = -3; % x的下界
x_ub = 3; % x的上界

%% 初始化粒子的位置和速度
x = zeros(n,narvs);
for i = 1: narvs
    x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1);    % 随机初始化粒子所在的位置在定义域内
end
v = -vmax + 2*vmax .* rand(n,narvs);  % 随机初始化粒子的速度（这里我们设置为[-vmax,vmax]）
%  注意：这种写法只支持2017及之后的Matlab，老版本的同学请自己使用repmat函数将向量扩充为矩阵后再运算。
% 即：v = -repmat(vmax, n, 1) + 2*repmat(vmax, n, 1) .* rand(n,narvs);  
% 注意：x的初始化也可以用一行写出来：  x = x_lb + (x_ub-x_lb).*rand(n,narvs) ，原理和v的计算一样
% 老版本同学可以用x = repmat(x_lb, n, 1) + repmat((x_ub-x_lb), n, 1).*rand(n,narvs) 

%% 计算适应度
fit = zeros(n,1);  % 初始化这n个粒子的适应度全为0
for i = 1:n  % 循环整个粒子群，计算每一个粒子的适应度
    fit(i) = Obj_fun1(x(i,:));   % 调用Obj_fun1函数来计算适应度（这里写成x(i,:)主要是为了和以后遇到的多元函数互通）
end
pbest = x;   % 初始化这n个粒子迄今为止找到的最佳位置（是一个n*narvs的向量）
ind = find(fit == max(fit), 1);  % 找到适应度最大的那个粒子的下标
gbest = x(ind,:);  % 定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量）

%% 在图上标上这n个粒子的位置用于演示
h = scatter(x,fit,80,'*r');  % scatter是绘制二维散点图的函数,80是我设置的散点显示的大小（这里返回h是为了得到图形的句柄，未来我们对其位置进行更新）

%% 迭代K次来更新速度与位置
fitnessbest = ones(K,1);  % 初始化每次迭代得到的最佳的适应度
for d = 1:K  % 开始迭代，一共迭代K次
    for i = 1:n   % 依次更新第i个粒子的速度与位置
        v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:));  % 更新第i个粒子的速度
        % 如果粒子的速度超过了最大速度限制，就对其进行调整
        for j = 1: narvs
            if v(i,j) < -vmax(j)
                v(i,j) = -vmax(j);
            elseif v(i,j) > vmax(j)
                v(i,j) = vmax(j);
            end
        end
        x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
        % 如果粒子的位置超出了定义域，就对其进行调整
        for j = 1: narvs
            if x(i,j) < x_lb(j)
                x(i,j) = x_lb(j);
            elseif x(i,j) > x_ub(j)
                x(i,j) = x_ub(j);
            end
        end
        fit(i) = Obj_fun1(x(i,:));  % 重新计算第i个粒子的适应度
        if fit(i) > Obj_fun1(pbest(i,:))   % 如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度
            pbest(i,:) = x(i,:);   % 那就更新第i个粒子迄今为止找到的最佳位置
        end
        if  fit(i) > Obj_fun1(gbest)  % 如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度
            gbest = pbest(i,:);   % 那就更新所有粒子迄今为止找到的最佳位置
        end
    end
    fitnessbest(d) = Obj_fun1(gbest);  % 更新第d次迭代得到的最佳的适应度
    pause(0.1)  % 暂停0.1s
    h.XData = x;  % 更新散点图句柄的x轴的数据（此时粒子的位置在图上发生了变化）
    h.YData = fit; % 更新散点图句柄的y轴的数据（此时粒子的位置在图上发生了变化）
end

figure(2)
plot(fitnessbest)  % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳的位置是：'); disp(gbest)
disp('此时最优值是：'); disp(Obj_fun1(gbest))

3、评价

这个模块的话说白了跟你们学校的综测评分机制差不多，不过这个一般参杂主观性太强，我们一开始学了，但是老师最后说不让我们用（好像是用了，就会给文章的质量大打折扣），就无语......

划重点：各位小伙伴在学的时候最好先咨询一下老师你们赛区的评分规则！

关于第一次比赛后的个人体会

7月1日下午，在结束了大一下学期的期末考试后，开始了为期一个多月的数学建模集训。本次比赛我们学校一共有15支队伍参赛，最后的正式比赛的时间为9月9日下午六点至9月12日晚上八点钟，历时74小时。

每支队伍有三个人组成，负责的工作主要有分析问题并建立数学模型、利用matlab等数学编程软件编写代码跑数据、写论文等，其中数学建模论文分为论文标题、摘要、问题的重述、模型假设、模型的建立、模型的求解、模型检验、模型的分析与评估、参考文献以及附录等十个方面，论文的好坏会直接影响最后能否获奖。

每支队伍的三个同学可以相互协商分工，我当时主要负责算法和编程这块以及辅助分析问题和建立数学模型。暑期的集训时间非常紧张，需要在有限的时间掌握文献检索、算法学习、分析问题的模型、以及latex的论文编写、还有最重要的一点就是队友之间的磨合，这个在最后比赛的三天起着非常大的作用，所以在寻找队友的时候要考虑到这一点。我当时的两个队友都是通过数学竞赛认识的，大家都比较熟，合作起来会比较容易。

集训期间每天会有老师来上一些课程，每天大约只有五六个小的时间是在上课的，其余时间都是自主学习，并且在集训期间无特殊情况几乎不会放假的，这个对参赛选手的意志力具有一定的挑战性。

当时为了节省时间直接在比赛的教室打地铺

数学建模比赛需要每一位参赛选手都认真、努力的去完成题目，甚至需要废寝忘食的精神。比赛期间指导老师会安排比赛场地，我们学校是每个组一个教室，在影像楼的四五楼。关于作息时间的安排是因组而异的，当时我们组为了节约时间，直接带上草席、被子去比赛场地打地铺，学累了就躺在被子上睡一会，然后起来接着干，我当时是比赛期间的三个晚上基本上是处于凌晨三点睡六点起的状态，在严重压缩睡眠时间的同时还要保持白天清醒的工作状态就需要自己提前准备好“物资”，当时比赛期间我是买了很多咖啡和功能饮料，这些是比赛期间续命的“装备”。这三天的比赛节奏一定要把控好，因为本科组是ABC三个选题，三选一，每个选题都有三至四个小问，我们当时选的是C题，题目给了一个word文档里面有四个小问和一个有十多万组数据的excel表格。

当时跑数据的时候CPU在燃烧

比赛期间尽量在第一天的时候要完成选题和把握题目整体思路的工作，第二天需要完成第一小问，第二小问要基本完成，第三天需要开始题目的收尾工作，第四天需要不断修改论文，打磨文章，在解决问题的同时，写论文的同学要紧跟建模和编程的同学，这样才能把握好比赛的节奏。在最后一天的下午我们基本上写完了论文，经过一遍又一遍的检查，修改自己的结题论文，最后提前半个小时交掉了结题论文。

三天的比赛终于结束了！！！

在10月10号的时候结果出来了，老天不负有心哇，最后拿到了奖，对于第一次参赛的我们莫不是一次极大的鼓舞。

最后，我想说的是数模比赛虽然具有一定的难度，需要付出大量的时间和精力去为比赛做准备，但其含金量也是众所周知。参赛前需要提前了解数模竞赛的相关事项再去寻找志同道合的队友一起参赛。希望有更多的同学加入建模这个大家庭，共同努力、共同学习、共同进步，增进友谊，团结协作，勇于创新，一起为学校贡献自己的一份力量。