【机器学习】03 激活函数 （详细注释+动态训练效果图)

前面的两篇文章
【机器学习】01 梯度下降（详细注释+动态训练效果图)
【机器学习】02 两个参数的梯度下降 （详细注释+动态训练效果图)
在前面的学习中我们已经让我们的人工智能学习到了蘑菇大小和毒性的关系。精确是很精确，但是，这似乎并不是一个智慧生物思考时常见的模型。比如说我们人类在思考问题的时候，往往不会产生精确的数值估计，而更倾向于分类问题，比如说米饭的多少和饱腹程度的关系，在现实生活中，我们往往会说3两饭我吃不饱，四两饭刚刚好，最多说一句三两饭大概是8分饱，而没有刻画出一个饭的两数和饱腹程度的精确曲线。换句话说，贴标签相对于精确计算更符合我们的生物本能，即人类思考问题的方式往往是离散的分类而不是精确的拟合。对于我们的人工智能也是一样的，若能精确地估算出不同大小的豆豆的毒性固然是好事，但一般会采用更加干脆的分类，比如毒性为0.7以上的蘑菇是毒蘑菇，而毒性为0.7以下的为无毒蘑菇。

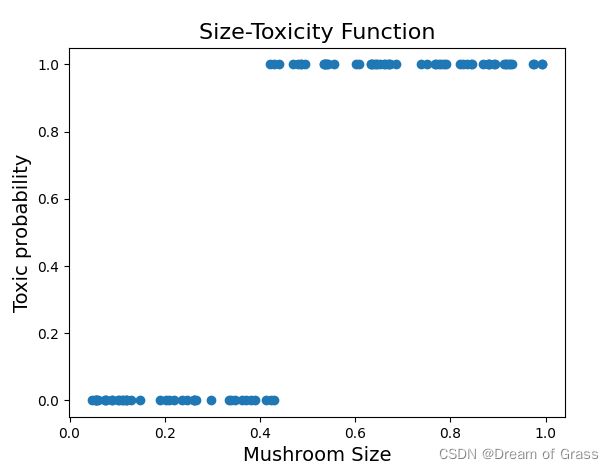
那么从有毒和无毒的角度来看，我们的关系图其实是这样的。

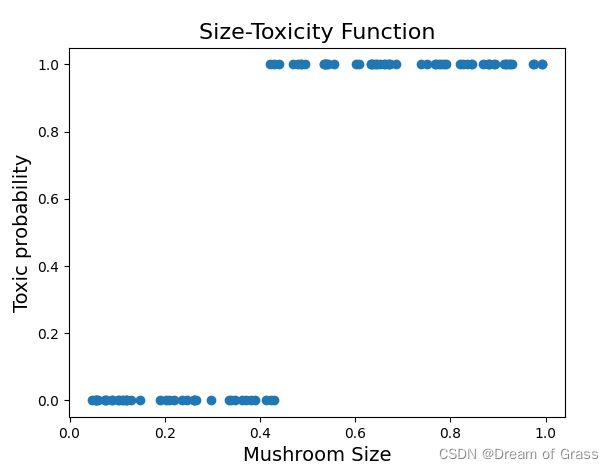
注意这个时候的纵坐标就是有毒概率了，而不是之前的毒性大小了。

很明显，如果数据变成了上面这种形式，之前的预测模型就无能为力了。不过，我们可以给之前的预测函数的结果在进行一个变化，比如放到一个分段函数中去，就可以实现非黑即白的分类效果了。

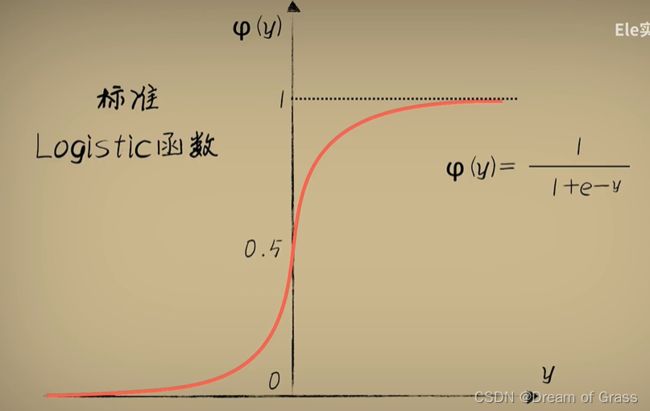
其实上面所说的分段函数就是传说中的激活函数了。

现在用的比较普遍的激活函数就是Sigmoid函数了。

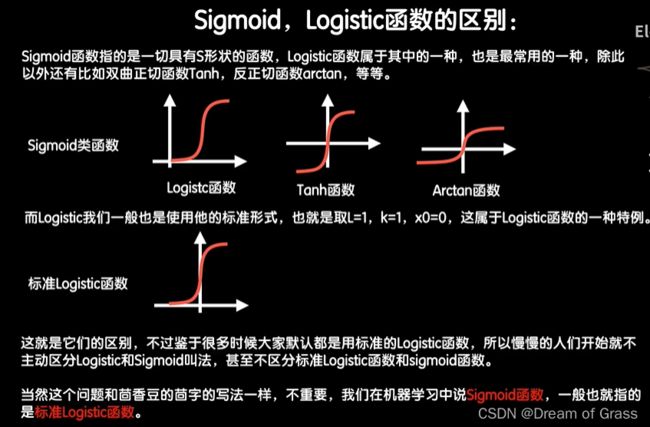
也就是说，现在我们最终预测出来的结果是$a=sigmoid(wx+b)$，当然了完整公式就是$$a=\frac{1}{e^{-wx+b}}$$

误差的公式就是$$e=(y-a{)}^2$$

后面我们一样进行梯度下降，还是求a对w和b的偏导，只是这时候的求法和前面不一样。我们可以看到，上面的这个公式比较复杂，直接求导比较麻烦，所以我们就用小学一年级学过的复合函数求导的链式法则来进行求导。

实际操作

生成非黑即白的数据集

通过一个逻辑盘来生成数据集

import numpy as np

def get_mushroom(counts):
	xs = np.random.rand(counts)
	xs = np.sort(xs)
	ys = np.zeros(counts)
	for i in range(counts):
		x = xs[i]
		yi = 0.7*x+(0.5-np.random.rand())/50+0.5
		if yi > 0.8:
			ys[i] = 1
	return xs,ys

随便给一个预测函数

# 随便给出一个预测函数
w = 1.2
b=-0.5
z=w*xs+b
a=1/(1+np.exp(-z))
# print(y_pre)
plt.plot(xs, a, color='green')
plt.show()

随便给一个预测函数

# 随便给出一个预测函数
w = 1.2
b=-0.5
z=w*xs+b
a=1/(1+np.exp(-z))
# print(y_pre)
plt.plot(xs, a, color='green')
plt.show()

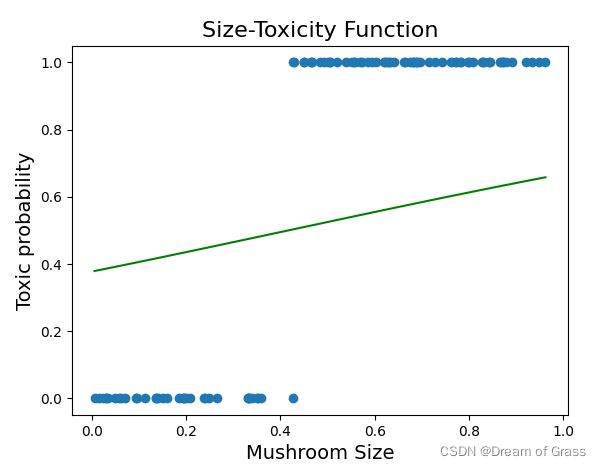
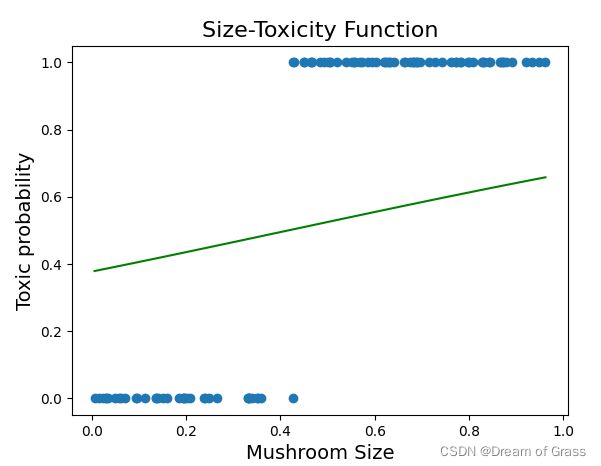
现在我们看到的这条绿色的线感觉和之前的直线没什么区别，其实是因为这个曲线的曲率太小了，导致看上去和直线差不多。不过之后在我们的动态效果图里就可以看到它慢慢“现出原形”了！

梯度下降代码

for _ in range(5000):
    for i in range(beans_num):
        x = xs[i]
        y = ys[i]
        # 用链式法则来求导
        z=w*x+b
        a=1/(1+np.exp(-z))
        e=(y-a)**2

        deda=-2*(y-a)
        dadz=a*(1-a)
        dzdw=x
        dzdb=1

        dedw=deda*dadz*dzdw
        dedb=deda*dadz*dzdb
        alpha = 0.05
        # 学习率
        w = w - alpha * dedw
        b=b-alpha*dedb

这一步就是将前面的求导过程转化为代码就行了。

动态训练效果图

    # 下面是利用 matplotlib 来画一个动态图，画出参数不断调整的过程
    if _%10==0:
        plt.clf()
        # 清空窗口
        plt.scatter(xs, ys,color='moccasin')
        z = w * xs+b
        a=1/(1+np.exp(-z))
        # print(y_pre)
        plt.plot(xs, a, color='crimson')
        # 这里的误差就要用ys-a而不是之前的ys-z
        es = (ys - a) ** 2
        avg_e = np.sum(es) / beans_num
        plt.xlim(0,1)
        plt.ylim(0,1.2)
        plt.text(0, 0.87, "误差:",color="mediumturquoise",font='STSong',fontsize=14)
        plt.text(0.1, 0.87, avg_e,color="mediumblue",font='STSong',fontsize=15)
        plt.text(0.03,1.13,"w:",color="teal",font='STSong',fontsize=14)
        plt.text(0.1,1.13,w,color="teal",font='STSong',fontsize=14)
        plt.text(0.03, 1, "b:", color="teal", font='STSong', fontsize=14)
        plt.text(0.1, 1, b, color="teal", font='STSong', fontsize=14)
        plt.pause(0.0001)

plt.show()

完整代码

import numpy as np
from matplotlib import pyplot as plt
import dataset

beans_num = 100
xs, ys = dataset.get_mushroom(beans_num)
# print(xs)
# print(ys)
# 画一个散点图，看看豆豆的大小和毒性大致是一个什么关系
plt.scatter(xs, ys)
# 画个标题和横纵坐标
plt.title("Size-Toxicity Function", fontsize=16)
plt.xlabel("Mushroom Size", fontsize=14)
plt.ylabel("Toxic probability", fontsize=14)
# plt.show()

# 随便给出一个预测函数
w = 1.2
b=-0.5
z=w*xs+b
a=1/(1+np.exp(-z))
# print(y_pre)
plt.plot(xs, a, color='green')
plt.show()

# 上面还是错的离谱，下面使用梯度下降算法来修正w

# 普通随机下降
for _ in range(5000):
    for i in range(beans_num):
        x = xs[i]
        y = ys[i]
        # 用链式法则来求导
        z=w*x+b
        a=1/(1+np.exp(-z))
        e=(y-a)**2

        deda=-2*(y-a)
        dadz=a*(1-a)
        dzdw=x
        dzdb=1

        dedw=deda*dadz*dzdw
        dedb=deda*dadz*dzdb
        alpha = 0.05
        # 学习率
        w = w - alpha * dedw
        b=b-alpha*dedb

    # 下面是利用 matplotlib 来画一个动态图，画出参数不断调整的过程
    if _%10==0:
        plt.clf()
        # 清空窗口
        plt.scatter(xs, ys,color='moccasin')
        z = w * xs+b
        a=1/(1+np.exp(-z))
        # print(y_pre)
        plt.plot(xs, a, color='crimson')
        # 这里的误差就要用ys-a而不是之前的ys-z
        es = (ys - a) ** 2
        avg_e = np.sum(es) / beans_num
        plt.xlim(0,1)
        plt.ylim(0,1.2)
        plt.text(0, 0.87, "误差:",color="mediumturquoise",font='STSong',fontsize=14)
        plt.text(0.1, 0.87, avg_e,color="mediumblue",font='STSong',fontsize=15)
        plt.text(0.03,1.13,"w:",color="teal",font='STSong',fontsize=14)
        plt.text(0.1,1.13,w,color="teal",font='STSong',fontsize=14)
        plt.text(0.03, 1, "b:", color="teal", font='STSong', fontsize=14)
        plt.text(0.1, 1, b, color="teal", font='STSong', fontsize=14)
        plt.pause(0.0001)

plt.show()