找规律之动态规划系列
动态规划
- 前言
- 一、案例
- 二、题解
- 总结
- 参考文献
- 附录
-
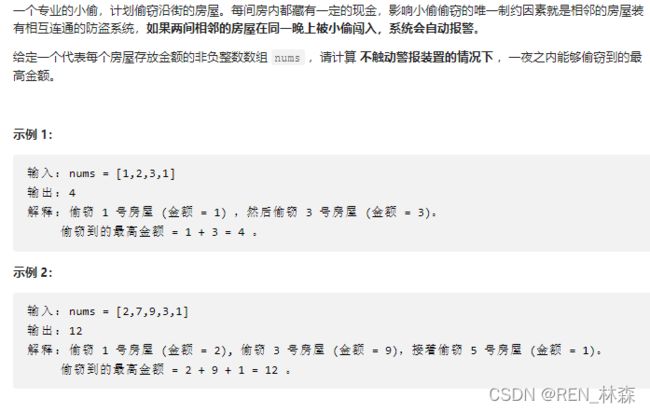
- 1、房屋偷盗
- 2、房屋偷盗之环形房
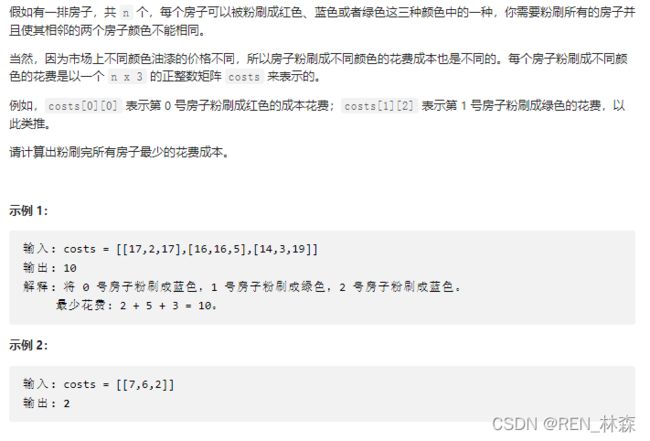
- 3、粉刷房子
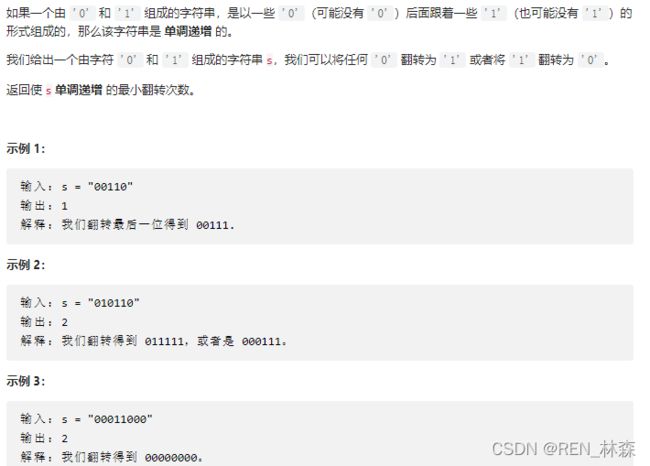
- 4、翻转字符
-
- 总结
- 5、最长斐波那契数列
- 6、最少回文分割
- 7、最长公共子序列(经典二维动规)
前言
模拟作为暴力解并不是解决问题的唯一解,而找到问题里的规律,可以避免很多无意义的暴力。把大问题拆成很多相关联的小问题,其中的关联就是规律,规律是一种规划,规律在小问题之前传递就是动态的,即动态规划。
一、案例
二、题解
每次都只能走一步或两步,所以到达每一个台阶都是由前两个台阶的最小值通过跳一步或者跳两步到达当前台阶,如此反复,直到所有台阶跳完,这个时候取上一个台阶所需花费和上两个台阶所需花费的最小值,即跳完的最低消费。
//找其中的规律,用动态规划解题。
public int minCostClimbingStairs2(int[] cost) {
int dp1 = 0, dp2 = 0;
for (int i : cost) {
int dp = dp1 < dp2 ? dp1 + i : dp2 + i;
dp1 = dp2;
dp2 = dp;
}
return dp1 < dp2 ? dp1 : dp2;
}
当然,我们来看看暴力法,可以不断DFS,选花费最低的那条路径的和,但是很多路径是没有意义的。
//DFS快速解题
public int minCostClimbingStairs(int[] cost) {
dfs(cost, -1, 0);
return min;
}
private void dfs(int[] cost, int cur, int sum) {
if (cur >= cost.length) {
min = min < sum ? min : sum;
return;
}
dfs(cost, cur + 1, sum + (cur == -1 ? 0 : cost[cur]));
dfs(cost, cur + 2, sum + (cur == -1 ? 0 : cost[cur]));
}
int min = Integer.MAX_VALUE;
总结
1)如果能把题分解成多个前后关联的小问题,那么就知道怎么去实现动态性,找到具体的关联是什么,就知道怎么实现规划。
参考文献
[1] LeetCode 爬楼梯的最少成本
附录
1、房屋偷盗
//动态规划,偷一个房间时存的金额大小只跟前面第2个和第3个有关,中间必须间隔一个或两个。看最后一个和倒数第二个谁大取谁。
public int rob(int[] nums) {
int dp1 = 0, dp2 = 0, dp3 = 0;
for (int num : nums) {
int dp = Math.max(dp1, dp2) + num;
dp1 = dp2;
dp2 = dp3;
dp3 = dp;
}
return dp2 < dp3 ? dp3 : dp2;
}
2、房屋偷盗之环形房
//环形房子
//吃什么受什么苦不是关键,成长核心在于一点一点的学习和思考去积累。
public int rob2(int[] nums) {
if (nums.length == 1) return 0;
int dp1 = 0, dp2 = 0, dp3 = 0;
for (int i = 0; i < nums.length - 1; i++) {
int dp = Math.max(dp1, dp2) + nums[i];
dp1 = dp2;
dp2 = dp3;
dp3 = dp;
}
int m1 = Math.max(dp2, dp3);
dp1 = dp2 = dp3 = 0;
for (int i = 1; i < nums.length; i++) {
int dp = Math.max(dp1, dp2) + nums[i];
dp1 = dp2;
dp2 = dp3;
dp3 = dp;
}
int m2 = Math.max(dp2, dp3);
return m1 < m2 ? m2 : m1;
}
3、粉刷房子
package com.xhu.offer.offerII;
//粉刷房子
public class MinCost {
//动态规划,给房子刷成什么颜色,要看前面一个房子除了现在颜色之外的最低花费。
//换句话说,就是当前选什么颜色之和前一个选什么颜色所花费的开销有关。
public int minCost(int[][] costs) {
int[][] dp = new int[3][2];
for (int[] cost : costs) {
int[] newDp = new int[]{Math.min(dp[1][1], dp[2][1]), Math.min(dp[0][1], dp[2][1]), Math.min(dp[0][1], dp[1][1])};
for (int i = 0; i < 3; i++) dp[i][1] = newDp[i] + cost[i];
}
return Math.min(dp[0][1], Math.min(dp[1][1], dp[2][1]));
}
//优化,减少一点空间
public int minCost2(int[][] costs) {
int[] dp = new int[3];//让下标代替三种颜色
for (int[] cost : costs) {
int[] newDp = new int[]{dp[1] < dp[2] ? dp[1] : dp[2], dp[0] < dp[2] ? dp[0] : dp[2], dp[0] < dp[1] ? dp[0] : dp[1]};
for (int i = 0; i < 3; i++) dp[i] = newDp[i] + cost[i];
}
return dp[0] < dp[1] ? dp[0] < dp[2] ? dp[0] : dp[2] : dp[1] < dp[2] ? dp[1] : dp[2];
}
}
4、翻转字符
package com.xhu.offer.offerII;
//翻转字符
public class MinFlipsMonoIncr {
//从0到每个字符所行成的子字符串需翻转的次数之和前一个字符有关。翻转之后有序。
public int minFlipsMonoIncr(String s) {
//以0结尾最少翻转次数为dp0,以1结尾最少翻转次数为dp1;都是在有序的基础上。
int len = s.length();
int dp0 = 0, dp1 = 0;
for (int i = 0; i < len; i++) {
int v = s.charAt(i) - '0';
if (v == 1) {
dp1 = Math.min(dp0, dp1);
dp0++;
continue;
}
dp1 = Math.min(dp0, dp1) + 1;
}
return Math.min(dp0, dp1);
}
}
总结
1)动态规划的状态定义很重要,如该题,dp0表示从0到当前字符的以0结尾的最小翻转数,dp1表示以0到当前字符的以1结尾的最小翻转数。
5、最长斐波那契数列
package com.xhu.offer.offerII;
import java.util.HashMap;
import java.util.Map;
//最长斐波拉契数列
public class LenLongestFibSubseq {
//hashmap处理+动态规划(往后遍历,每加一个元素,都要看前面那两个元素符合,所以需要固定一个元素,所以双循环,另一元素确定用map快速查找)
public int lenLongestFibSubseq(int[] arr) {
int len = arr.length, ans = 0;
Map<Integer, Integer> cache = new HashMap<>();//map解决前面可能符合条件太多的状态,以O(1)快速找到,而不是一个一个去试。
int[][] dp = new int[len][len];//i到j的最长斐波拉契数列
for (int i = 0; i < len; i++) {
for (int j = i + 1; j < len; j++) {
dp[i][j] = 2;
int gap = arr[j] - arr[i];
if (cache.containsKey(gap)) {
int l = cache.get(gap);
dp[i][j] = dp[l][i] + 1;
ans = Math.max(ans, dp[i][j]);
}
cache.put(arr[i], i);
}
}
return ans < 3 ? 0 : ans;
}
}
6、最少回文分割
//dp1 + dp2
//dp1:int[][] dp1 = new int[][];dp1[i][j]状态定义:[j,i]区间的字符串是否为回文。状态转移:dp[i-1][j+1]为回文且ch[i] == ch[j]时,为1.
//dp2:int[] dp2 = new int[];dp2[i]状态定义:[0,i]的最小回文个数。
public int minCut(String s) {
int len = s.length();
int[][] dp1 = new int[len][len];
for (int i = 0; i < len; i++) {
for (int j = i; j >= 0; j--) {
if (s.charAt(i) == s.charAt(j) && (i == j || i - 1 == j || dp1[i - 1][j + 1] == 1)) dp1[i][j] = 1;
}
}
int[] dp2 = new int[len + 1];
for (int i = 1; i <= len; i++) {
dp2[i] = i;
for (int j = 0; j < i; j++) {
if (dp1[i - 1][j] == 1) {
dp2[i] = Math.min(dp2[i], dp2[j] + 1);
}
}
}
return dp2[len] - 1;
}
7、最长公共子序列(经典二维动规)
package com.xhu.offer.offerII;
public class LongestCommonSubsequence {
//二维动态规划
public int longestCommonSubsequence(String text1, String text2) {
//状态定义:dp[i][j]表示text1[0,i]和text2[0,j]的公共子串。
int m = text1.length(), n = text2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
char chT1 = text1.charAt(i - 1);
for (int j = 1; j <= n && j <= i; j++) {
char chT2 = text2.charAt(j - 1);
if (chT1 == chT2) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
//思路总结:
//拿text1的第0到i所行成的子字符串去和text2匹配,一共匹配text1.len次。
//每次新来的text1[i]去和text[j]匹配,根据两字符是否相等来确定当前两子字符串的最长公共子串。
}