DFS模拟方面案例
DFS模拟方面
- 前言
- 案例
- 题解
- 总结
- 参考文献
- 附录
-
- 1、含有重复元素集合的组合
- 2、全排列
- 3、含有重复元素集合的全排列
-
- 总结
- 4、括号匹配
- 5、分割回文子字符串
-
- 总结
- 6、复原 IP
-
- 总结
前言
DFS的应用很广,比如二叉树、多叉树、图、包括一些排列组合问题。主要还是排列组合问题,用DFS去模拟,但是时间复杂度,还有函数栈的开销。
案例
题解
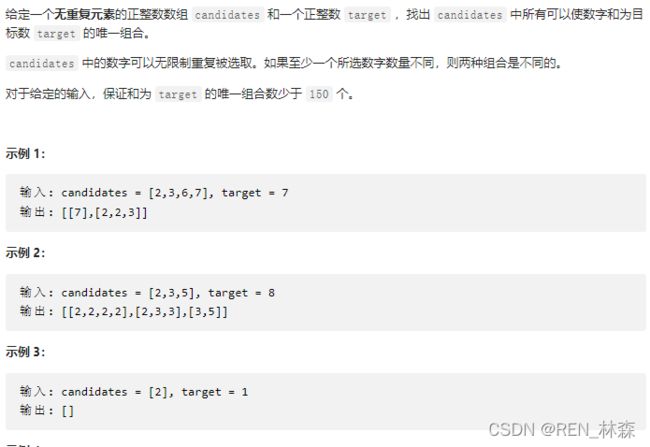
1)允许重复选择元素的组合
//数字可以重复使用
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<Integer> el = new ArrayList<>();
recursion(candidates, 0, 0, target, el);
return res;
}
private void recursion(int[] candidates, int cur, int sum, int target, List<Integer> el) {
if (sum >= target) {
if (sum == target) res.add(new ArrayList<>(el));
return;
}
int len = candidates.length;
for (int i = cur; i < len; i++) {
el.add(candidates[i]);
recursion(candidates, i + 1, sum + candidates[i], target, el);
el.remove(el.size() - 1);
}
}
2)含有 k 个元素的组合
package com.xhu.offer.offerII;
import java.util.ArrayList;
import java.util.List;
//含有K个元素的组合
public class Combine {
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
List<Integer> el = new ArrayList<>();
recursion(0, n, k, el);
return res;
}
private void recursion(int cur, int n, int k, List<Integer> el) {
if (el.size() == k) {
res.add(new ArrayList<>(el));
return;
}
for (int i = cur + 1; i <= n; i++) {
el.add(i);
recursion(i, n, k, el);
el.remove(el.size() - 1);
}
}
}
总结
1)DFS模拟哪些无法用多层循环解决的循环问题,模拟为暴力法的一种,但其含有递归的思想。
参考文献
[1] LeetCode 允许重复选择元素的组合
[2] LeetCode 含有 k 个元素的组合
附录
补充案例
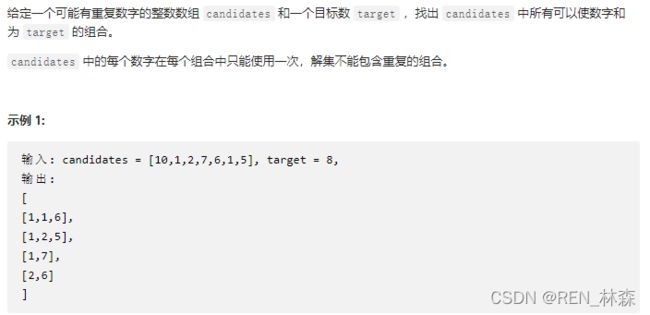
1、含有重复元素集合的组合
//每个数字只能用一次
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<Integer> el = new ArrayList<>();
Arrays.sort(candidates);
recursion(candidates, -1, 0, target, el);
return res;
}
private void recursion(int[] candidates, int cur, int sum, int target, List<Integer> el) {
if (sum >= target) {
if (sum == target) res.add(new ArrayList<>(el));
return;
}
int len = candidates.length;
int pre = -1;
for (int i = cur + 1; i < len; i++) {
if(pre == candidates[i]) continue;
el.add(candidates[i]);
recursion(candidates, i + 1, sum + candidates[i], target, el);
pre = el.get(el.size() - 1);
el.remove(el.size() - 1);
}
}
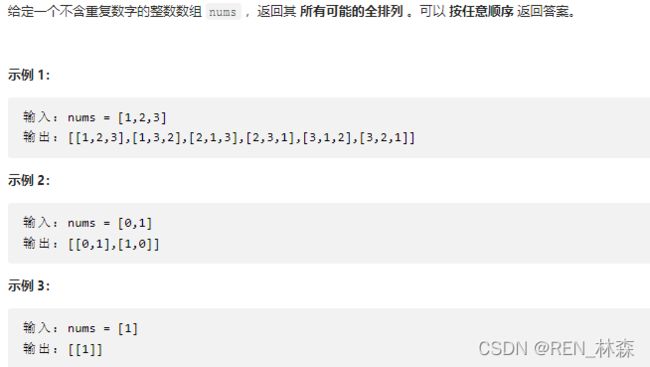
2、全排列
package com.xhu.offer.offerII;
import java.util.ArrayList;
import java.util.List;
//全排列
public class Permute {
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
List<Integer> el = new ArrayList<>();
int[] mark = new int[nums.length];
recursion(nums, el, mark);
return res;
}
private void recursion(int[] nums, List<Integer> el, int[] mark) {
int len = nums.length;
if (el.size() == len) {
res.add(new ArrayList<>(el));
return;
}
for (int i = 0; i < len; i++) {
if (mark[i] == 1) continue;
el.add(nums[i]);
mark[i] = 1;
recursion(nums, el, mark);
el.remove(el.size() - 1);
mark[i] = 0;
}
}
}
3、含有重复元素集合的全排列
如何去重?重复的原因在于该位置上前一个元素和当前元素是一样的,那么DFS下去就一定会重复。所以可通过排序+设置pre来去重,配合回溯完成解题。

//排序+回溯+设置pre来高效去重,毕竟下个位置还要放以前相同的元素那肯定会重复。
List<List<Integer>> re = new ArrayList<>();
//总结:好好调试,可能比以前的SystemOut更快发现问题,从而理清思路。
//总结:做不出来的时候可能太累了,思路较乱,可以恢复平静,减慢思考速度,慢慢一步一步重新理清思路。
public List<List<Integer>> permuteUnique(int[] nums) {
List<Integer> el = new ArrayList<>();
int[] mark = new int[nums.length];
Arrays.sort(nums);
recursion(nums, el, mark);
return re;
}
private void recursion(int[] nums, List<Integer> el, int[] mark) {
int len = nums.length;
if (el.size() == len) {
re.add(new ArrayList<>(el));
return;
}
int pre = -11;
for (int i = 0; i < len; i++) {
if (mark[i] == 1 || pre == nums[i]) continue;
el.add(nums[i]);
mark[i] = 1;
recursion(nums, el, mark);
el.remove(el.size() - 1);
mark[i] = 0;
pre = nums[i];
}
}
总结
1)好好调试,可能比以前的SystemOut更快发现问题,从而理清思路。
2)做不出来的时候可能太累了,思路较乱,可以恢复平静,减慢思考速度,慢慢一步一步重新理清思路。
4、括号匹配
package com.xhu.offer.offerII;
import java.util.ArrayList;
import java.util.List;
//括号生成
public class GenerateParenthesis {
//回溯
//内在规则,最终,左括号数 = 右括号数;左边的括号数一定要大于等于右括号数;左边的括号数不能超过n;
//左右括号数相等于n时完成DFS,其它情况就视为DFS失败,剪枝。
List<String> res = new ArrayList<>();
public List<String> generateParenthesis(int n) {
recursion(n, 0, 0);
return res;
}
StringBuilder sb = new StringBuilder();
private void recursion(int n, int l, int r) {
if (l < r) return;
if (l == n && r == n) {
res.add(sb.toString());
return;
}
//可填左括号
if (l < n || l == r) {
sb.append('(');
recursion(n, l + 1, r);
sb.delete(sb.length() - 1, sb.length());
}
sb.append(')');
recursion(n, l, r + 1);
sb.delete(sb.length() - 1, sb.length());
}
}
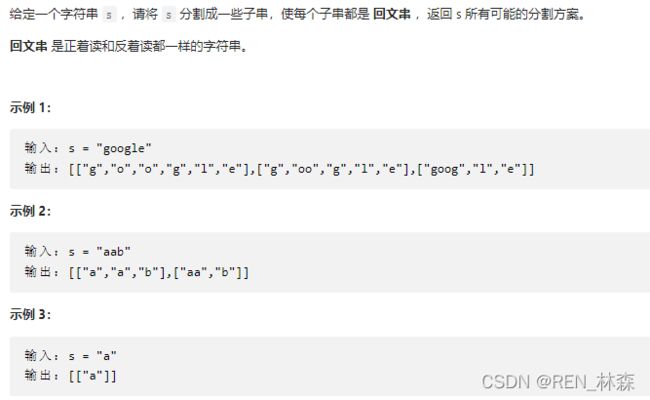
5、分割回文子字符串
package com.xhu.offer.offerII;
import java.util.ArrayList;
import java.util.List;
//分割回文子字符串
public class Partition {
//动态规划预处理+DFS匹配
public String[][] partition(String s) {
//预处理从i到j区间是否为回文
int len = s.length();
int[][] dp = new int[len][len];
for (int i = 0; i < len; i++) {
for (int j = i; j >= 0; j--) {
if (s.charAt(i) == s.charAt(j) && (i == j || i - 1 == j || dp[i - 1][j + 1] == 1)) dp[i][j] = 1;
}
}
//DFS
dfs(s, dp, 0);
//处理结果并返回
String[][] r = new String[res.size()][];
int cnt = 0;
for (List<String> re : res) {
r[cnt] = new String[re.size()];
int count = 0;
for (String s1 : re) {
r[cnt][count++] = s1;
}
cnt++;
}
return r;
}
List<List<String>> res = new ArrayList<>();
List<String> el = new ArrayList<>();
private void dfs(String s, int[][] dp, int cur) {
if (cur == s.length()) {
res.add(new ArrayList<>(el));
return;
}
for (int i = 0; i + cur < s.length(); i++) {
if (dp[cur + i][cur] == 0) continue;
//是回文才往el里面加这个回文字符串。
el.add(s.substring(cur, cur + 1 + i));
dfs(s, dp, cur + i + 1);
el.remove(el.size() - 1);
}
}
//调试:
//p1:dp没处理好,就是j = i - 1的时候,不需要dp[i-1][j+1],它永远为0。
//p2:dfs的出口条件问题,不应该el.size() == s.length(),而是cur走到len的时候cur==s.length(),毕竟el里是长度不一的字符串。
public static void main(String[] args) {
String s = "google";
new Partition().partition(s);
}
}
总结
1)这个题一开始是做不来的,但是应用之前的总结,实在思路不同就马上看题解,不浪费时间,也不折磨自己浪费精力。看到了题解的提示:动态规划预处理+DFS遍历,这两个我都懂,但是这个题一开始就没想到,可能一下子就被复杂到了。
2)以dp预处理+DFS的提示,我应用前面总结的放慢心态,慢慢理清思路,便独立自主的写出来该题,但还是有两个bug。
3)基于bug,我应用前面总结的sout只是大概定位那个部件出错,以调试的方式快速匹配和我脑中逻辑不一样的地方,快速修改掉第一个bug,dp错误问题。
4)结果还是不对,问题肯定处在DFS,只有一个结果,说明递归出口多半有问题,定位递归出口,发现递归出口不对,快速改掉第二个bug,完成解题。
6、复原 IP
package com.xhu.offer.offerII;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
//复原IP
public class RestoreIpAddresses {
//和拆解成多少回文字符串一样,那里是满足是否为回文,这里是满足是否为不含前导为0且转化为的数字在0-255之间。
//dp+DFS
public List<String> restoreIpAddresses(String s) {
int len = s.length();
int[][] dp = new int[len][len];
//dp
for (int i = 0; i < len; i++) {
for (int j = i; j >= 0; j--) {
//超过三位数肯定大于255,而且后面的都大于3位数了,直接break。
if (i - j > 2) break;
//前导为0的肯定不行,只能看看后面是否有希望
if (s.charAt(j) == '0' && i != j) continue;
//筛选0-255的数字
int m = Integer.parseInt(s.substring(j, i + 1));
if (m <= 255) dp[i][j] = 1;
}
}
for (int[] ints : dp) {
System.out.println(Arrays.toString(ints));
}
//dfs
dfs(s, dp, 0, 0);
return res;
}
List<String> res = new ArrayList<>();
StringBuilder sb = new StringBuilder();
//总结:急解决不了问题,反而会导致思路乱起来停滞不前,没有将压力转化为动力,而是压力自然变成了巨大无比的阻力。该调试调试,该理思路理思路...
//错了不要急,急解决不了问题,该干嘛干嘛,急功近利可不行,成长需要沉淀,沉淀需要把时间高效利用起来,而不是停滞不前。
private void dfs(String s, int[][] dp, int cur, int level) {
if (level == 4) {
if (cur == s.length()) res.add(sb.delete(sb.length() - 1, sb.length()).toString());//去掉最后的点
return;
}
for (int i = 0; i + cur < s.length(); i++) {
if (dp[cur + i][cur] == 0) continue;
sb.append(Integer.parseInt(s.substring(cur, cur + 1 + i))).append('.');
dfs(s, dp, cur + 1 + i, level + 1);
sb.delete(cur + level, sb.length());//bug1:直接从cur删是有问题的,没有考虑加的点所占的位置。
}
}
//调试
//p1:dp有问题,dp[4][3]应该为0,因为s="01".bug在于dp中s.charAt(j) == 0,应该是=='0';
public static void main(String[] args) {
new RestoreIpAddresses().restoreIpAddresses("010010");
}
}
总结
1)急解决不了问题,反而会导致思路乱起来停滞不前,没有将压力转化为动力,而是压力自然变成了巨大无比的阻力。该调试调试,该理思路理思路…
2)错了不要急,急解决不了问题,该干嘛干嘛,急功近利可不行,成长需要沉淀,沉淀需要把时间高效利用起来,而不是停滞不前。
3)前面刷题的经验的应用起来,刷题顺畅多了,没思路看题解,有思路不对就调试。