隐马尔可夫模型基础介绍

应用场景

隐含马尔可夫模型（Hidden Markov Model, 简称HMM）可以被应用到语音，人脸识别，动作识别等领域。语音具有时序性质。HMM被应用到语音当中，可以有效的反映出语音的时序变化。人脸图像在水平方向和垂直方向上都表现出了像素级的顺序性，因此HMM可以被用来人脸识别，对周围环境的变化也具有很好的鲁棒性。除此以外，人的行为动作等，也表现出序列性。

模型定义

隐含马尔克夫模型中的变量可以被分为状态变量和观测变量。状态变量是不可观测，也叫做隐藏的，被称为隐藏变量。我们将状态变量表示为：
$$y_1,y_2,\cdots ,y_i,\cdots ,y_n$$
其中$y_i\in \mathcal{Y}$表示第$i$时刻的状态值，表示状态空间$\mathcal{Y}$。一般情况下，存在多个状态值，并且状态之间具有转换，我们将所有的状态表示为:
$$\{s_1,s_2,\cdots ,s_i,\cdots ,s_N\}$$
其中$N$表示状态空间中可能取值的数量。我们将观测变量表示为:
$$\{x_1,x_2,\cdots ,x_i,\cdots ,x_n\}$$
其中$x_i\in \mathcal{X}$表示第$i$时刻的观测值，并且$x_i$可以是连续值，也可以是离散值。假定$\mathcal{X}$的取值范围为
$$\{o_1,o_2,\cdots ,o_i,\cdots ,o_M\}$$

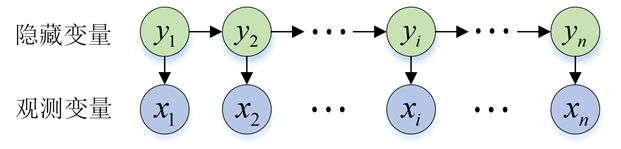
针对图所示，变量之间的联合概率分布表示为：
$$P(x_1,y_1,\cdots ,x_i,y_i\cdots ,x_n,y_n)=P(y_1)P(x_1|y_1)\prod _{i=2}^{n}P(y_i|y_{i-1})P(x_i|y_i)$$

马尔科夫模型的确定需要三组参数：
（1）初始状态的概率：
给定时间，在初始时间不同状态出现的概率被称为初始状态概率。初始状态的概率通常记作：
$$\{{\pi }_1,{\pi }_2,\cdots ,{\pi }_i,\cdots ,{\pi }_n\}$$
其中${\pi }_i=P(y_1=s_i)$，$i\in [1,N]$ 。
（2）状态转移的概率：
任意两个状态$i$和$j$之间的转移概率记作：
$$a_{ij}$$
其中$a_{ij}=P(y_{t+1}=s_j|y_t=s_i)$， $i,j\in [1,N]$，由$a_{ij}$组成的矩阵记作$\mathbf{A}$。
（3）输出观测的概率：
基于当前状态得到的观测值概率记作：
$$b_{ij}$$
其中$b_{ij}=P(x_t=o_j|y_t=s_i)$，$i\in [1,N]$ ，$j\in [1,M]$ ，由 $b_{ij}$组成的矩阵记作$\mathbf{B}$ 。 通过上述三组参数就可以确定一个隐马尔科夫模型。我们用 表示模型，记：
$\lambda =[\mathbf{A},\mathbf{B},\pi ]$
具有顺序性的东西，都可以使用HMM模型。

HMM实例

有三种天气，晴天，阴天和雨天，我们分别使用0,1,2表示晴天阴天和雨天。天气之间的转化概率我们使用矩阵$\mathbf{A}$来表示，即状态转移概率矩阵，如下所示：

	晴天	阴天	雨天
晴天	0.33	0.33	0.33
阴天	0.33	0.33	0.33
雨天	0.33	0.33	0.33

我们已知一个普遍的现象，下雨天很少出去游玩，所以天气和是否出去游乐园具有一定的关系。我们使用矩阵$\mathbf{B}$表示各种天气下进行相关活动的概率，即输出观测概率，如下所示：

	去游乐园	不去游乐园
晴天	0.73	0.27
阴天	0.45	0.55
雨天	0.25	0.75

我们已知第0天的天气概率如下所示，我们使用$\pi$表示，即初始状态概率：

	第0天天气概率
晴天	0.5
阴天	0.3
雨天	0.2

按照时间以天为单位进行观察，得到5天的活动序列如下所示：

1天	2天	3天	4天	5天
去游乐园	去游乐园	不去游乐园	去游乐园	不去游乐园
0	0	1	0	1

HMM实例

在实际的应用场景中，我们非常关注隐马尔可夫模型的三个基本问题：
评估问题：给定模型$\lambda =[\mathbf{A},\mathbf{B},\pi ]$，通过什么样的方法可以评估模型$\lambda$和观测序列之间的匹配程度。或者是计算 $P(\mathbf{x}|\lambda )$，即在给定模型下，观测序列的概率，对应于穷举算法，前向算法，后向算法。
学习问题：给定观测序列，如果训练模型可以更好的表现观测数据。即给定观测序列，调整模型$\lambda =[\mathbf{A},\mathbf{B},\pi ]$，是得$P(\mathbf{x}|\lambda )$最大，对应于前向算法，后向算法。
解码问题：给定观测写和模型$\lambda =[\mathbf{A},\mathbf{B},\pi ]$，通过什么样的方法找到与观测序列最匹配的状态序列或模型的隐藏状态，对应于韦特比（Viterbi）算法。

HMM应用于中文分词任务

HMM对于中文分词，实际就是用来HMM中的维特比算法。HMM分词任务还是一种监督学习的方法。

步骤

1. 做label, B(Begin) M(Middle) E(End) S(Single)，基于监督任务，已经分好的词。
2. 初始化初始概率值，状态转移矩阵，观测矩阵。

        #初始化后的状态转移矩阵self.A为, B, M, S, E与B, M, S, E关系的一个二维矩阵，矩阵中的元素值为0。
        #初始化的概率self.pi为{B:0.0, M:0.0, S:0.0, E:0.0}
        #初始化后的观测概率矩阵为：{B:{}, M:{}, S:, E:{}}

3. 通过统计的方法，计算A，B，pi，A仅仅是一个$4\times 4$的矩阵，B是每个状态到单个字的一个概率值。
4. 通过观测值，例如我们的一个句子是由不同的字构成的，然后确定最优的BMSE序列，然后依据BMSE序列就可以得到我们的最终的分词。

HMM实现的算法代码解读

class HMM(object):
    def __init__(self):
        # 状态值集合viterbi
        self.state_lists = ['B', 'M', 'E', 'S']
        # 状态转移概率
        self.A = {}
        # 观测概率
        self.B = {}
        # 初始概率
        self.pi = {}
        # 统计B, M, E, S状态出现的次数，并且求出相应的概率
        self.count_dict = {}

    def train(self, path):
        def init_parameters():
            for state in self.state_lists:
                #初始化状态转移概率
                self.A[state] = {s: 0.0 for s in self.state_lists}
                self.B[state] = {}
                #初始化初始概率
                self.pi[state] = 0.0
                self.count_dict[state] = 0

        def makeLabels(text):
            output = []
            if len(text) == 1:
                output.append('S')
            else:
                output += ['B'] + ['M'] * (len(text) - 2) + ['E']
            return output

        init_parameters()
        #初始化后的状态转移矩阵self.A为, B, M, S, E与B, M, S, E关系的一个二维矩阵，矩阵中的元素值为0。
        #初始化的概率self.pi为{B:0.0, M:0.0, S:0.0, E:0.0}
        #初始化后的观测概率矩阵为：{B:{}, M:{}, S:, E:{}}
        line_nums = 0

        with open(path, encoding='utf-8') as f:
            for line in f:
                line_nums += 1

                line = line.strip()
                if not line:
                    continue

			#得到一个一个的字
                word_lists = [i for i in line if i != ' ']
                line_list = line.split()
           
           #line_state保存了有监督的信息
                line_states = []
                for w in line_list:
                    line_states.extend(makeLabels(w))

                assert len(word_lists) == len(line_states)

                for k, v in enumerate(line_states):
                #统计B，M，S，E出现的次数
                    self.count_dict[v] += 1
                    if k == 0:
                        self.pi[v] += 1
                    else:
                        #k表示了第一个状态，v表示了当前状态，做状态转移次数的统计
                        self.A[line_states[k - 1]][v] += 1
                        #从状态到单词的次数统计
                        self.B[line_states[k]][word_lists[k]] = \
                            self.B[line_states[k]].get(word_lists[k], 0) + 1.0
        #self.pi中的结果和为1，行数是固定的，k和v的值要么是B，要么是S，只有这两个值是有数据的。
        self.pi = {k: v * 1.0 / line_nums for k, v in self.pi.items()}
        #将统计数据转移为概率
        self.A = {k: {k1: v1 / self.count_dict[k] for k1, v1 in v.items()} for k, v in self.A.items()}
        #将统计数据转移为概率，例如B一共出现了多少次，对于一个字的概率计算，B->字
        self.B = {k: {k1: (v1 + 1) / self.count_dict[k] for k1, v1 in v.items()} for k, v in
                      self.B.items()}
        return self

    def viterbi(self, text, states, start_p, trans_p, ober_p):
        """这是一个递推式算法，不需要迭代更新，套用Ver特比算法公式，求最优的BMSE的状态转移。
        text:要切分的句子
        states: B,M,E,S
        start_p:初始概率
        trans_p:转移概率矩阵
        ober_p:观测概率矩阵
        """
        V = [{}]
        path = {}
        for y in states:
            V[0][y] = start_p[y] * ober_p[y].get(text[0], 0)
            path[y] = [y]
        for t in range(1, len(text)):
            V.append({})
            newpath = {}
            never_find = text[t] not in ober_p['S'].keys() and \
                        text[t] not in ober_p['M'].keys() and \
                        text[t] not in ober_p['E'].keys() and \
                        text[t] not in ober_p['B'].keys()
            for y in states:
                emitP = ober_p[y].get(text[t], 0) if not never_find else 1.0
                (pro, state) = max(
                    [(V[t - 1][y0] * trans_p[y0].get(y, 0) * emitP, y0) for y0 in states if V[t - 1][y0] >= 0])
                V[t][y] = pro
                newpath[y] = path[state] + [y]
            path = newpath
        (pro, state) = max([(V[len(text) - 1][y], y) for y in ['E', 'S']])
        return pro, path[state]

    def cut(self, text):
        pro, pos_list = self.viterbi(text, self.state_lists, self.pi, self.A, self.B)
        begin = 0
        result = []
        for i, char in enumerate(text):
            pos = pos_list[i]
            if pos == 'B':
                begin = i
            elif pos == 'E':
                result.append(text[begin: i + 1])
            elif pos == 'S':
                result.append(char)

        return result

hmm = HMM()
hmm.train('./msr_training.utf8')
def text2index(path, cut=True):
   with open(path,encoding='utf-8') as f:
       dict = {}
       i = 0
       for line in f:
           line = line.strip()
           if cut:
               res = line.split()
           else:
               res = hmm.cut(line)
           dict[i] = []
           nums = 0
           for s in res:
               dict[i].append((nums, nums + len(s) - 1))
               nums += len(s)
           i += 1
#            print(dict)
   return dict


def evaluate(evaluate, gold):
   dict_evaluate = text2index(evaluate, cut=False)
   dict_gold = text2index(gold)

   linelen = len(dict_evaluate)
   assert len(dict_evaluate) == len(dict_gold)

   nums_evaluate = 0
   nums_gold = 0
   nums_correct = 0
   for i in range(linelen):
       seq_evaluate = dict_evaluate[i]
       seq_gold = dict_gold[i]
       nums_evaluate += len(seq_evaluate)
       nums_gold += len(seq_gold)
       for t in seq_evaluate:
           if t in seq_gold:
               nums_correct += 1

   P = nums_correct / nums_evaluate
   R = nums_correct / nums_gold
   F1 = 2*P * R / (P + R)
   return P, R, F1
hmm = HMM()
hmm.train('./msr_training.utf8')
text = '这是一个非常好的方案！'
res = hmm.cut(text)
print(text)
print(res)

P, R, F1 = evaluate('./msr_test.utf8', './msr_test_gold.utf8')
print("HMM的精确率：", round(P, 3))
print("HMM的召回率：", round(R, 3))
print("HMM的F1值：", round(F1, 3))