Learning Without Forgetting 笔记及实现
Learning Without Forgetting
-
- LWF简介
- 方法对比
- LWF算法流程
- 总结
- 实现
LWF简介
LWF是结合知识蒸馏(KD)避免灾难性遗忘的经典持续学习方法。本质上是通过旧网络指导的输出对在新任务训练的网络参数进行平衡,从而得到在新旧任务网络上都表现较好的性能。
方法对比
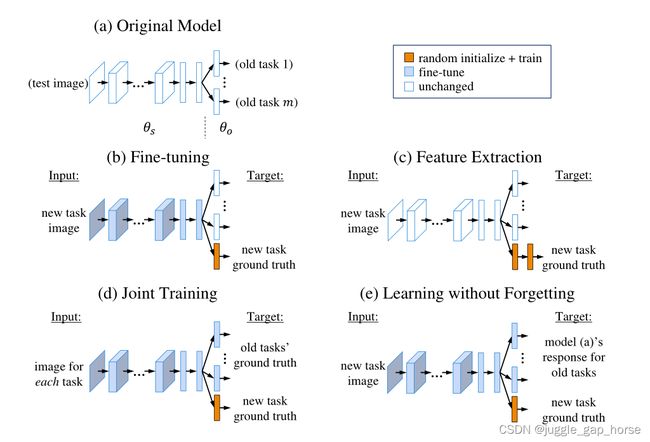
a.从头开始训练
b.微调:在旧任务的网络基础上以较小的学习率学习新任务 另一种意义上的initialization?
c.联合训练:使用所有任务的数据一起训练
d.特征提取:将旧任务的参数固定作为特征提取器,添加新的层训练新任务
LWF算法流程

θ s \theta_s θs为在old task上pretrained网络CNN的共享参数
θ o \theta_o θo为每个old task的特定参数(可理解为网络的i最后的classifier head)
( X n , Y n ) (X_n,Y_n) (Xn,Yn) new task的数据
初始化:
1.将新数据 ( X n , Y n ) (X_n,Y_n) (Xn,Yn) 输入在旧任务pretrained网络中得到一组respond Y o Y_o Yo
2.将new task对应的classifier head参数随机初始化(加快训练的常见手段)
训练:
Y o ^ \hat{Y_o} Yo^ 为待训练网络CNN 对应old task的输出,最开始 θ o \theta_o θo= θ o ^ \hat{\theta_o} θo^ , θ s \theta_s θs= θ s ^ \hat{\theta_s} θs^
Y n ^ \hat{Y_n} Yn^ 为待训练网络对应new task的输出,最开始 θ n \theta_n θn= θ n ^ \hat{\theta_n} θn^ , θ s \theta_s θs= θ s ^ \hat{\theta_s} θs^
优化目标为
θ s ∗ , θ o ∗ , θ n ∗ ← argmin θ ^ s , θ ^ o , θ ^ n ( λ o L o l d ( Y o , Y ^ o ) + L n e w ( Y n , Y ^ n ) + R ( θ ^ s , θ ^ o , θ ^ n ) ) \theta_{s}^{*}, \theta_{o}^{*}, \theta_{n}^{*} \leftarrow \underset{\hat{\theta}_{s}, \hat{\theta}_{o}, \hat{\theta}_{n}}{\operatorname{argmin}}\left(\lambda_{o} \mathcal{L}_{o l d}\left(Y_{o}, \hat{Y}_{o}\right)+\mathcal{L}_{n e w}\left(Y_{n}, \hat{Y}_{n}\right)+\mathcal{R}\left(\hat{\theta}_{s}, \hat{\theta}_{o}, \hat{\theta}_{n}\right)\right) θs∗,θo∗,θn∗←θ^s,θ^o,θ^nargmin(λoLold(Yo,Y^o)+Lnew(Yn,Y^n)+R(θ^s,θ^o,θ^n))
第一项可以理解为old task的子优化目标,第二项为new task的优化目标,第三项为正则化项。
可以发现整个训练过程和joint training很相似,但是最大的不同是LWF没有用到old task data,而是巧妙地用KD损失去平衡old task的性能。至于KD则体现在以下公式:
L o l d ( y o , y ^ o ) = − H ( y o ′ , y ^ o ′ ) = − ∑ i = 1 l y o ′ ( i ) log y ^ o ′ ( i ) \begin{aligned} \mathcal{L}_{o l d}\left(\mathbf{y}_{o}, \hat{\mathbf{y}}_{o}\right) &=-H\left(\mathbf{y}_{o}^{\prime}, \hat{\mathbf{y}}_{o}^{\prime}\right) \\ &=-\sum_{i=1}^{l} y_{o}^{\prime(i)} \log \hat{y}_{o}^{\prime(i)} \end{aligned} Lold(yo,y^o)=−H(yo′,y^o′)=−i=1∑lyo′(i)logy^o′(i)
l l l 是label的数量,而 y ^ o ′ ( i ) \hat{y}_{o}^{\prime(i)} y^o′(i) 和 y o ′ ( i ) y_{o}^{\prime(i)} yo′(i) 是 y ^ o ( i ) \hat{y}_{o}^{(i)} y^o(i) 和 y o ( i ) {y}_{o}^{(i)} yo(i) 的修正版本,也就是这里体现了KD的概念, y o ′ ( i ) y_{o}^{\prime(i)} yo′(i) 是soft target,而 y ^ o ′ ( i ) \hat{y}_{o}^{\prime(i)} y^o′(i) 为网络预测概率值。
y o ′ ( i ) = ( y o ( i ) ) 1 / T ∑ j ( y o ( j ) ) 1 / T , y ^ o ′ ( i ) = ( y ^ o ( i ) ) 1 / T ∑ j ( y ^ o ( j ) ) 1 / T y_{o}^{\prime(i)}=\frac{\left(y_{o}^{(i)}\right)^{1 / T}}{\sum_{j}\left(y_{o}^{(j)}\right)^{1 / T}}, \quad \hat{y}_{o}^{\prime(i)}=\frac{\left(\hat{y}_{o}^{(i)}\right)^{1 / T}}{\sum_{j}\left(\hat{y}_{o}^{(j)}\right)^{1 / T}} yo′(i)=∑j(yo(j))1/T(yo(i))1/T,y^o′(i)=∑j(y^o(j))1/T(y^o(i))1/T
所以网络在训练时,第一部分的loss使得网络的输出概率值一定程度上贴近old task
总结
LWF其实质上是结合了KD和微调,优势在于训练相比joint training更快,且不需要访问先前的数据。但连续学习多个任务仍然避免不了灾难性遗忘
实现
以下是基于pytorch的简单复现,废话不多说贴上code
# 准备数据集
n_classes = 10 # split_mnist数据集一共10类
n_tasks = 5
per_classes_task = int(n_classes / n_tasks)
split_mnist = SplitMNIST(n_experiences=n_tasks, seed=0,
return_task_id=True, shuffle=False)
train_dataset = split_mnist.train_stream[0].dataset
test_dataset = split_mnist.test_stream[0].dataset
train_loader = torch.utils.data.DataLoader(
train_dataset, batch_size=128, shuffle=True)
test_loader = torch.utils.data.DataLoader(
test_dataset, batch_size=1000, shuffle=True)
训练旧任务
def kaiming_normal_init(m):
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, nonlinearity='relu')
elif isinstance(m, nn.Linear):
nn.init.kaiming_normal_(m.weight, nonlinearity='sigmoid')
def train(epoch, model, optimizer, criterion):
print('\nEpoch: %d' % epoch)
model.train()
train_loss = 0.0
correct = 0
total = 0
for batch_id, (x, y, t) in enumerate(train_loader):
x, y = x.to(device), y.to(device)
optimizer.zero_grad()
y_pred = model(x)
loss = criterion(y_pred, y)
loss.backward()
optimizer.step()
train_loss += loss.item()
_, y_pred = y_pred.max(1)
total += len(y)
correct += y_pred.eq(y).sum().item()
progress_bar(batch_id, len(train_loader), 'Loss: %.3f | Acc: %.3f%% (%d/%d)'
% (train_loss / (batch_id + 1), 100. * correct / total, correct, total))
return train_loss / (batch_id + 1)
def test(epoch, model, criterion):
global best_acc
model.eval()
test_loss = 0.0
correct = 0
total = 0
with torch.no_grad():
for batch_id, (x, y, t) in enumerate(test_loader):
x, y = x.to(device), y.to(device)
y_pred = model(x)
loss = criterion(y_pred, y)
test_loss = loss.item()
_, y_pred = y_pred.max(1)
total += len(y)
correct += y_pred.eq(y).sum().item()
progress_bar(batch_id, len(test_loader), 'Loss: %.3f | Acc: %.3f%% (%d/%d)'
% (test_loss / (batch_id + 1), 100. * correct / total, correct, total))
acc = 100. * correct / total
if acc > best_acc:
print('Saving..')
state = {
'model': model.state_dict(),
'acc': acc,
'epoch': epoch,
}
if not os.path.isdir('checkpoint'):
os.mkdir('checkpoint')
torch.save(state, './checkpoint/ckpt_mnist.pth')
best_acc = acc
return acc
# 训练和测试
device = 'cuda' if torch.cuda.is_available() else 'cpu'
epochs = 10
best_acc = 0.0
lr = 0.01
pre_model = SimpleMLP(num_classes=per_classes_task, hidden_size=256).to(device)
print(pre_model)
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(pre_model.parameters(), lr=lr,
momentum=0.9, weight_decay=5e-4)
for epoch in range(epochs):
train(epoch, pre_model, optimizer, criterion)
test(epoch, pre_model, criterion)
LWF
split_mnist = SplitMNIST(n_experiences=n_classes, seed=0,
return_task_id=True, shuffle=False)
# 取第2个2分类任务
train_dataset = split_mnist.train_stream[1].dataset
test_dataset = split_mnist.test_stream[1].dataset
# 取第1个2分类任务测试LWF在旧任务上的性能
val_dataset = split_mnist.test_stream[0].dataset
train_loader = torch.utils.data.DataLoader(
train_dataset, batch_size=128, shuffle=True)
test_loader = torch.utils.data.DataLoader(
test_dataset, batch_size=1000, shuffle=True)
val_loader = torch.utils.data.DataLoader(
val_dataset, batch_size=1000, shuffle=True)
net_new = SimpleMLP(num_classes=per_classes_task, hidden_size=256).to(device)
net_old = SimpleMLP(num_classes=per_classes_task, hidden_size=256).to(device)
oor = torch.load('checkpoint/ckpt_mnist.pth')
net_new.load_state_dict(oor['model'])
net_old.load_state_dict(oor['model'])
incremental_class = per_classes_task
# 获取前一个任务模型的分类头数量
in_features = net_old.classifier.in_features
out_features = net_old.classifier.out_features
# 提取分类头中参数
weight = net_old.classifier.weight.data
bias = net_old.classifier.bias.data
# 新头数量
new_out_features = incremental_class + out_features
# 构建新分类器
new_fc = nn.Linear(in_features, new_out_features)
kaiming_normal_init(new_fc.weight)
# 新任务模型的前两个头被替换,剩余头用来学习新类
new_fc.weight.data[:out_features] = weight
new_fc.bias.data[:out_features] = bias
net_new.classifier = new_fc
net_new = net_new.to(device)
print('new head numbers:', net_new.classifier.out_features)
# 确保前一个任务模型不参与反向传播
for param in net_old.parameters():
param.requires_grad = False
改变训练,测试方法
def train(alpha, T, epoch):
print('\nEpoch: %d' % epoch)
net_new.eval()
train_loss = 0
correct = 0
total = 0
for batch_idx, (x, y, t) in enumerate(train_loader):
x, y = x.to(device), y.to(device)
optimizer.zero_grad()
outputs = net_new(x)
soft_y = net_old(x)
# 新类的Loss
loss1 = criterion(outputs, y)
outputs_S = F.softmax(outputs[:, :out_features] / T, dim=1)
outputs_T = F.softmax(soft_y[:, :out_features] / T, dim=1)
loss2 = outputs_T.mul(-1 * torch.log(outputs_S))
loss2 = loss2.sum(1)
loss2 = loss2.mean() * T * T
# loss = loss1 * alpha + loss2 * (1 - alpha)
loss = loss1 + alpha * loss2
loss.backward(retain_graph=True)
# loss.backward()
optimizer.step()
train_loss += loss.item()
_, y_pred = outputs.max(1)
total += len(y)
correct += y_pred.eq(y).sum().item()
progress_bar(batch_idx, len(train_loader), 'Loss: %.3f | Acc: %.3f%% (%d/%d)'
% (train_loss / (batch_idx + 1), 100. * correct / total, correct, total))
return train_loss / (batch_idx + 1)
def test(alpha, T, epoch):
global best_acc
net_new.eval()
test_loss = 0
correct = 0
total = 0
with torch.no_grad():
for batch_idx, (inputs, targets, t) in enumerate(test_loader):
inputs, targets = inputs.to(device), targets.to(device)
outputs = net_new(inputs)
soft_target = net_old(inputs)
loss1 = criterion(outputs, targets)
outputs_S = F.softmax(outputs[:, :out_features] / T, dim=1)
outputs_T = F.softmax(soft_target[:, :out_features] / T, dim=1)
loss2 = outputs_T.mul(-1 * torch.log(outputs_S))
loss2 = loss2.sum(1)
loss2 = loss2.mean() * T * T
loss = loss1 * alpha + loss2 * (1 - alpha)
test_loss += loss.item()
_, predicted = outputs.max(1)
total += len(targets)
correct += predicted.eq(targets).sum().item()
progress_bar(batch_idx, len(test_loader), 'Loss: %.3f | Acc: %.3f%% (%d/%d)'
% (test_loss / (batch_idx + 1), 100. * correct / total, correct, total))
acc = 100. * correct / total
if acc > best_acc:
print('Saving..')
state = {
'model': net_new.state_dict(),
'acc': acc,
'epoch': epoch,
}
if not os.path.isdir('checkpoint'):
os.mkdir('checkpoint')
torch.save(state, './checkpoint/LWF_ckpt.pth')
best_acc = acc
return acc
def val(epoch): # 用于测试旧任务
net_new.eval()
correct = 0
total = 0
with torch.no_grad():
for batch_idx, (inputs, targets, t) in enumerate(val_loader):
inputs, targets = inputs.to(device), targets.to(device)
outputs = net_new(inputs)
_, predicted_old = outputs.max(1)
total += len(targets)
correct += predicted_old.eq(targets).sum().item()
progress_bar(batch_idx, len(val_loader), 'Acc: %.3f%% (%d/%d)'
% (100. * correct / total, correct, total))
return 100. * correct / total
训练和测试
# 简单实现,超参非最佳参数
T = 2
alpha = 0.5 #
criterion = nn.CrossEntropyLoss()
best_acc = 0.0
optimizer = optim.SGD(filter(lambda p: p.requires_grad, net_new.parameters()), lr=0.01,
momentum=0.9, weight_decay=5e-4)
for epoch in range(epochs):
train_loss = train(alpha, T, epoch)
acc_new = test(alpha, T, epoch)
acc_old = val(epoch)
torch.save(net_new.state_dict(), 'model.pth')
论文地址