<论文阅读> 基于激光的人类跟随机器人的并排跟随 Laser-Based Side-by-Side Following for Human-Following Robots
论文地址:基于激光的人类跟随机器人的并排跟随
【摘要】:在结构化环境中,跟随人的移动机器人面临着目标人在走廊交叉口处转身时,被墙壁完全遮挡的挑战。这可能会导致目标在跟随机器人的视野范围内短期甚至永久丢失。针对该问题,提出了一种新的并行跟踪方法。在本文中,人类跟随机器人首先使用车载激光扫描仪检测目标人的腿和不同类型的走廊交叉口。然后,我们提供了一种走廊检测方法对目标和走廊交叉点之间的几何结构约束进行聚类。最后,为了增加目标人在走廊交叉口处转弯时的可见时间,结合激光信息设计了一种并排跟随腿跟踪器(SFLT)。走廊检测方法和SFLT方法已经在MATLAB中进行了仿真。此外,并排跟随的方法已经在走廊环境中的现实机器人操作系统(ROS)中实现。仿真和实际实验的结果表明,当移动机器人在走廊交叉路口遇到潜在的遮挡物时,我们的方法成功跟随率为92.0%。
I. 引言
人机协作或人机交互显示了人与机器人之间的和谐关系,机器人需要在同一自然空间内与目标人进行稳定、实时、安全的交互。作为典型的人机交互,人类跟随机器人(HFRs)保持跟随目标与机器人之间的相对距离和方向,在服务和辅助机器人 中发挥重要作用。在服务机器人的常见情况下,人类跟随机器人应该能够以合适的类人方式沿着其服务对象移动。
在过去的十年中,人类跟随机器人在使用 2D 激光进行人员检测和跟踪算法方面取得了重大进展。在许多室内实验和现场试验中,使用激光跟踪人的位置,因为它们比地板传感器更容易安装,所需的处理比视觉跟踪系统少得多,并且比 RFID 跟踪或 GPS 具有更高的精度。更具体地说,为了检测人的双腿,Montemerloet 等人可能是第一个提出基于激光的跟踪人的方法。最近,Chunget 通过利用人类行走模型来实现在遮挡下的稳健跟踪,建立了一种有效的腿部跟踪方案。Junget 在激光数据中定义人体特征并采用支持向量数据描述 (SVDD) 方法。Schulzet 引入基于样本的联合概率数据关联过滤器(SJPDAF)作为跟踪多个移动对象的新算法,该算法已被用于跟踪多个移动目标。缺点是 SJPDAF 方法的复杂性随着测量次数的增加而呈指数增长。但是,这些方法仅限于空旷和宽视野的环境。它们不适用于在狭窄的走廊中实现,因为墙壁会经常发生完全遮挡,例如图1。

为了克服图 1 中的问题,我们提出了一种新颖的并排跟踪方法,用于带有 2D 激光扫描仪的跟随机器人。一些研究人员在他们的社交机器人工作中开发了探索性并排跟踪策略。Moraleset 提出了一种基于人类行为观察的计算并排行走模型。结对行走时,下意识地保持并排排列是人类的一种自然习惯。对于朋友来说,这是一种更舒适的运动模式,而不是依次行走。但是,机器人和跟随目标需要实时共享目的地信息,这限制了跟随机器人的工作空间。此外,村上等人扩展了用于并排行走的扩展社会力模型的基本机制,在机器人不知道目的地的情况下实现了更好的并排性能。在我们的方法中,我们还预测了伙伴的行为,并在狭窄的通道中获得了更多的智能导航。Gonzaloet 提出了一种新颖的机器人社会感知导航框架,以安全和自然的方式与人并排行走拥挤的市区。此外,Repisoet 扩展了Social Force模型,并提出了一个新的框架,用于跟随机器人和城市环境中的陪伴。此外,没有考虑目标人的完全遮挡,尤其是目标人物在走廊的交叉路口转弯。
在21-22中已经很好地讨论了人在走廊环境中的任务,他们使用基于视觉的跟随机器人,提取目标的特征并通过它们来控制机器人的运动。通过这些方法,机器人计算速度和加速度信号以调整靠墙位置,例如,Dorbalaetal 开发了卷积神经网络 (CNN) 来直接估计图像所需的控制信号,这是在轮椅跟随机器人中实现的,这种方法的弱点在于它需要大量的计算能力和时间来训练图像数据。为克服这一挑战,Yuan 结合了基于势场的人体跟踪器和多假设拓扑图,可以在很大程度上避免激光扫描仪对目标的遮挡。
在本文中,考虑并排跟踪走廊环境的任务。本文的主要贡献如下:
- 建议使用走廊检测器来识别目标的一对腿和走廊交叉口之间的几何约束。使用此方法,当目标靠近走廊交叉口时触发并排跟随。
- 并排跟随腿跟踪器 (SFLT) 旨在实现机器人从目标背面到侧面的比例微分 (PD) 控制技术。这样,当目标人在走廊交叉口处转弯时,机器人可以保持长期视野。
本文分为五个部分。在其余四个部分中,第二部分描述了支持向量域描述 (SVDD) 方法来对人腿的检测和聚类。此外,走廊检测器旨在检测和评估走廊交叉点。在第三部分中,并排跟踪腿跟踪。在第四部分,使用两轮差分跟踪移动机器人,评估我们方法的性能。
II. 走廊检测器
A.人在走廊环境中的跟踪任务
图 2 显示了传统人类跟随方法中的激光扫描仪点的细节。当目标人在走廊交叉口右转被蓝色挡板遮挡时,激光扫描仪信息。通过观察图 2,我们可以推断,增加视野是克服任务的重要关键。此外,我们提出的并排方法可以确保整个过程目标在机器人的视野中。
 然而,触发并排跟随的第一步是识别目标人和机器人之间的几何约束。因此,设计了基于目标和墙壁之间的几何约束的走廊检测器方法(图 2 中的蓝色挡板)。走廊检测器方法包括两部分:(a)人腿检测,(b)走廊检测。
然而,触发并排跟随的第一步是识别目标人和机器人之间的几何约束。因此,设计了基于目标和墙壁之间的几何约束的走廊检测器方法(图 2 中的蓝色挡板)。走廊检测器方法包括两部分:(a)人腿检测,(b)走廊检测。
B.人体腿部检测
我们的机器人系统中使用的激光扫描仪是 Pepperl+FuchsR2000-B23 LiDAR 传感器。凭借其 360° 测量角度,此 LiDAR 传感器通过提供每秒 84,000 个扫描点和低至 0.043° 的角度分辨率来满足特定机器人应用的要求,以确保精确的对象轮廓。如第一节所述,有成熟的腿部检测算法可用于识别人的腿(例如,AdaBoost、SVDD、SJPDAF)。本文采用SVDD腿检测方法对目标人的腿对进行聚类。
图 3 显示了对人腿的激光扫描仪点进行聚类的 SVDD 方法。我们假设 m m m 点是从腿集群中获取的, D D D 被定义为两个连续点之间的距离。Chungetal 定义了三个属性来检测人腿:
- 第一个是关于从 P 1 P_1 P1 到 P m i n P_{min} Pmin 的集群中相邻点的周长 ( G i ) (G_i) (Gi) 。
- 第二个大约是腿簇的宽度 ( W i ) (W_i) (Wi),即从 P 1 P_1 P1 到 P m P_m Pm 的距离。
- 最后一个属性是 d e p t h ( H i ) depth(H_i) depth(Hi),即 P i P_i Pi 和 P 1 P m ‾ \overline{P_1P_m} P1Pm之间的最大距离。

我们使用 Heron 的公式来获得三角形的面积 Δ P 1 P j P m ΔP_1P_jP_m ΔP1PjPm。
Heron 公式:假设在平面内,有一个三角形,边长分别为 a 、 b 、 c a、b、c a、b、c,三角形的面积 S S S可由以下公式求得: S = p ( p − a ) ( p − b ) ( p − c ) S = {\sqrt {p(p-a)(p-b)(p-c)}} S=p(p−a)(p−b)(p−c)而公式里的 p p p为半周长(周长的一半)。
人腿的特征可以由以下等式定义:
{ G i = ∑ j = 1 m − 1 ∣ P j P j + 1 ‾ ∣ W i = ∣ P 1 P m ‾ ∣ H i = m a x 2 m ( m − W i ) ( m − ∣ P 1 P j ∣ ) ( m − ∣ P j P m ∣ ) W i (1) \begin{cases} G_i = \sum_{j=1}^{m-1}\lvert \overline{P_jP_{j+1}} \rvert \\\\ W_i = \lvert \overline{P_1P_m} \rvert \\\\ H_i = max{2 \sqrt{m(m-W_i)(m- \lvert P_1P_j \rvert)(m- \lvert P_jP_m \rvert)} \over W_i}\end{cases} \tag{1} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧Gi=∑j=1m−1∣PjPj+1∣Wi=∣P1Pm∣Hi=maxWi2m(m−Wi)(m−∣P1Pj∣)(m−∣PjPm∣)(1)
其中 m = ( W i + ∣ P 1 P j ∣ + ∣ P j P m ∣ ) 2 m={(W_i+|P_1P_j|+|P_jP_m|) \over 2} m=2(Wi+∣P1Pj∣+∣PjPm∣)。最优特征空间由以下等式创建:
m i n L ( R 2 , a , ξ ) = R + C ∑ i = 1 n ξ i s . t . ∥ x i − a ∥ 2 ≤ R 2 + ξ i , ξ i ≥ 0 , ∀ i , x i = ( G i W i H i ) (2) minL(R^2,a,\xi) = R+C\sum_{i=1}^n\xi_i \quad \quad s.t.\lVert x_i -a \rVert^2 \leq R^2 + \xi_i,\xi_i \geq 0,\forall_i,x_i = \begin{pmatrix} G_i \\ W_i \\ H_i \\ \end{pmatrix} \tag{2} minL(R2,a,ξ)=R+Ci=1∑nξis.t.∥xi−a∥2≤R2+ξi,ξi≥0,∀i,xi=⎝⎛GiWiHi⎠⎞(2)
在 (2) 中, n n n 是属性空间中的数据点总数。为了对 n n n 个扫描点进行分类,我们通过拉格朗日方程最小化中心 a a a 描述的球体半径 R R R。通过拉格朗日方程。 ξ i \xi_i ξi 表示松弛变量,参数 C C C 指定了球体体积和错误数之间的权衡。通过这种方式,我们获得了在激光扫描仪中的一对腿。
拉格朗日方程, L ( x , y , λ ) = f ( x , y ) + λ φ ( x , y ) L(x,y,\lambda) = f(x,y)+\lambda \varphi(x,y) L(x,y,λ)=f(x,y)+λφ(x,y),用于求解极值。
C.走廊检测
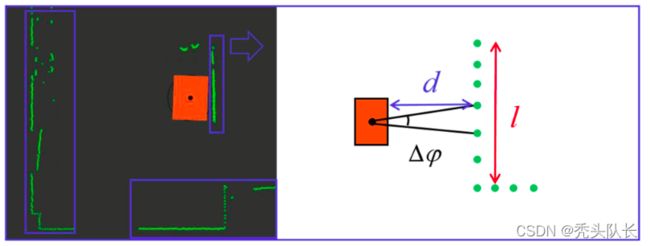
我们的贡献之一是我们设计了一种新颖的走廊检测器来检测走廊交叉点。为了匹配走廊的特征,我们将激光扫描仪点的数量描述为图4中的簇。由于相邻的激光扫描点分布均匀,当我们将机器人与墙壁之间的距离设置为 d d d时,墙壁上的扫描点数 n n n可以近似计算如下:
n = l d × s i n Δ φ (3) n = {l \over d \times sin \Delta \varphi} \tag{3} n=d×sinΔφl(3)
其中, l l l 是墙的宽度, Δ φ \Delta \varphi Δφ是角度分辨率。我们选择值 n n n 的最大值和最小值,进一步获取走廊交叉点处激光点的合理间隔,如 [ n m i n , n m a x ] [n_{min},n_{max}] [nmin,nmax]。
分析几何约束的类型,墙壁和走廊交叉口符合线性类型。此外,我们建议的走廊探测器应该检测所有集群的线性度。机器人和走廊交叉口之间的距离使用均方误差 (MSE) 计算。
{ y = a x + b a = y ‾ − b x ‾ , b = S x y S x x (4) \begin{cases} y = ax +b \\ a = \overline y - b \overline x,b = {S_{xy} \over S_{xx}} \end{cases} \tag{4} {y=ax+ba=y−bx,b=SxxSxy(4)
我们使用最小二乘法计算数据聚类中的线性拟合和线性度
{ S x y = ∑ x i y i − ( ∑ x i ∑ y i ) n S x x = ∑ x i 2 − ( ∑ x i ) 2 n x ‾ = ∑ x i n , y ‾ = ∑ y i n (5) \begin{cases} S_{xy} = \sum x_iy_i - {(\sum x_i\sum y_i)\over n} \\ S_{xx} = \sum x^2_i - {(\sum x_i)^2 \over n} \\ \overline x = {\sum x_i \over n}, \overline y = {\sum y_i \over n} \end{cases} \tag{5} ⎩⎪⎨⎪⎧Sxy=∑xiyi−n(∑xi∑yi)Sxx=∑xi2−n(∑xi)2x=n∑xi,y=n∑yi(5)
为了评估分类结果,我们根据计算它的相似度得分H。
H = e x p [ − a 1 ⋅ ∣ l ^ − l ∣ l − a 2 ( 1 − ∣ Q ∣ ) − a 3 ⋅ d d m ] (6) H = exp[-a_1 \cdot{\lvert \hat{l} - l \rvert \over l} - a_2(1-\lvert Q \rvert) - a_3 \cdot {d \over d_m}] \tag{6} H=exp[−a1⋅l∣l^−l∣−a2(1−∣Q∣)−a3⋅dmd](6)
其中 a 1 + a 2 + a 3 = 1 a1+a2+a3=1 a1+a2+a3=1, l l l 是墙的宽度, l ^ \hat l l^ 是拟合线段的长度, d d d 是机器人与墙之间的距离, d m d_m dm 激光扫描仪的最大检测范围,并且 Q Q Q 是相关系数 0 ≤ Q ≤ 1 0≤Q≤1 0≤Q≤1。当 ∣ Q ∣ → 1 |Q|→1 ∣Q∣→1时,数据越接近拟合线,数据分布越好,越接近线性。 R R R 的定义如下:
{ Q = S x y S x x S x y S y y = ∑ y i 2 − ( ∑ y i 2 ) n (7) \begin{cases} Q = {S_{xy} \over \sqrt{S_{xx} S_{xy}}}\\ S_{yy} = \sum y_i^2 - {(\sum y_i^2) \over n} \end{cases} \tag{7} ⎩⎨⎧Q=SxxSxySxySyy=∑yi2−n(∑yi2)(7)
通过使用人腿检测和走廊检测,可以轻松区分人腿和走廊交叉口。
III. 并排跟随腿追踪器
为了实现并排跟随方法,我们提出了一个强大的自适应控制器,命名为并排跟随腿跟踪器,旨在保持目标人和机器人之间的相对距离和方向。与传统的人类跟随方法不同,新的跟随方法使机器人保持在目标的侧面,而不是在目标后面。这样,机器人在跟随目标的同时增加了视野。
A.噪声滤波器和位置预测
所有检测到集群的位置是使用卡尔曼滤波器单独跟踪的,同时,我们使用卡尔曼滤波器来降低测量和预测位置的噪声,在跟踪的过程中,我们根据这个滤波器去扫描所有的集群,定义为: X k j \mathcal X_k^j Xkj,其中在2D激光的扫描仪中,位置、速度、加速度被定义为: X k j = [ x , y , x ˙ , y ˙ , x ¨ , y ¨ ] T \mathcal X_k^j = [x,y,\dot x,\dot y,\ddot x,\ddot y]^T Xkj=[x,y,x˙,y˙,x¨,y¨]T,在第二部分检测人腿和走廊之后,我们将所有的活动轨迹定义为状态估计 X k = X k 1 , X k 2 , . . . , X k N k \mathcal X_k = \mathcal X_k^1,\mathcal X_k^2,...,\mathcal X_k^{N_k} Xk=Xk1,Xk2,...,XkNk,这里 N k N_k Nk 是在 k k k 时刻所有轨迹的数量。
在我们的系统中,一个新的轨迹被刷新和初始化为 0 m / s 0 m/s 0m/s,进行中的轨迹进行如下更新:
{ x ( k ) = A x ( k − 1 ) + B u ( k ) + W ( k ) z ( k ) = H x ( k ) + V ( k ) (8) \begin{cases} x(k) = Ax(k-1) + B u(k) + W(k) \\ z(k) = Hx(k) + V(k) \end{cases} \tag{8} {x(k)=Ax(k−1)+Bu(k)+W(k)z(k)=Hx(k)+V(k)(8)
其中 U ( k ) U(k) U(k)是系统的控制变量, V ( k ) V(k) V(k)和 W ( k ) W(k) W(k)是(8)中过程和测量方程的噪声向量。另外, X ( k ) X(k) X(k)是机器人系统状态, A A A是状态矩阵, z ( k ) z(k) z(k)是观测向量, H H H是观测矩阵,定义如下:
X ( k ) = [ x , y , x ˙ , y ˙ , x ¨ , y ¨ ] T \mathcal X(k)= [x,y,\dot x,\dot y,\ddot x,\ddot y]^T X(k)=[x,y,x˙,y˙,x¨,y¨]T Z ( k ) = [ x y ] \mathcal Z(k)= \begin{bmatrix} x \\ y \\ \end{bmatrix} Z(k)=[xy] H = [ 1 0 0 0 0 0 0 1 0 0 0 0 ] \mathcal H= \begin{bmatrix} 1 & 0 & 0&0&0&0 \\ 0 & 1 & 0&0&0&0 \\ \end{bmatrix} H=[100100000000]
在公式8中, B B B和 U k U_k Uk为空,观测矩阵H只包括位置信息。对于噪声,过程噪声 W ( k ) W(k) W(k)假定为高斯白噪声,对角协防差矩阵 Q ′ = 1 0 − 8 Q' = 10^{-8} Q′=10−8,同时观测噪声 V ( k ) V(k) V(k)被设置为 R ′ = 1 0 − 1 R' = 10^{-1} R′=10−1。
B.角度控制
为了实现并排跟随,我们使用PD 控制器调整左轮 v L v_L vL 和右轮 v R v_R vR 的速度控制两轮移动机器人。
C. 并排跟随腿部跟踪器

如图 6 所示,并排跟随腿跟踪器 (SFLT) 被提出来克服人类在狭窄环境中跟随的挑战。 SFLT 是一种灵活而强大的控制器,以跟随或并排跟随的形式控制机器人,分为三个步骤:
- Step1,在正常工作条件下,机器人跟在目标后面。
- Step2,当目标靠近走廊路口时,机器人触发并排跟随走廊探测器。由于墙位于目标右侧,机器人保持左侧并排跟随目标人
- Step3,目标转弯后,很明显机器人会跟在目标后面,因为目标的转弯半径小于机器人。
V. 结论
这项工作提出了一种新的方法,在腿高度使用激光扫描仪用于并排跟随走廊环境。为了解决在走廊交叉口丢失目标的挑战,机器人系统集成了走廊检测器和并排的跟随腿跟踪器。详细地,走廊检测器计算线性度以评估走廊交叉口的相似度得分,并排跟随腿跟踪器使用 PD 控制器触发并排跟随运动控制在目标人员在走廊交叉口转弯时。为了评估我们的方法,两个贡献都在 Matlab 上进行了模拟,并在两轮移动机器人上实现。